Jan Techter (TU Berlin)
joint work with Niklas Affolter (TU Wien) and Felix Dellinger (TU Wien)
ICERM 2025
Various established discretizations of parametrized surfaces in DDG:
- Principal nets / curvature line parametrizations:
circular nets, conical nets, principal contact element nets - Kœnigs nets:
BS-Kœnigs nets, D-Kœnigs nets. - Isothermic nets:
circular isothermic nets, S-isothermic nets, S-conical nets - ...
Goal:
Unify, generalize, and improve established discretizations.
Still satisfy
Unify, generalize, and improve established discretizations.
Still satisfy
- transformation group principle
- cosistency priciple
- ...
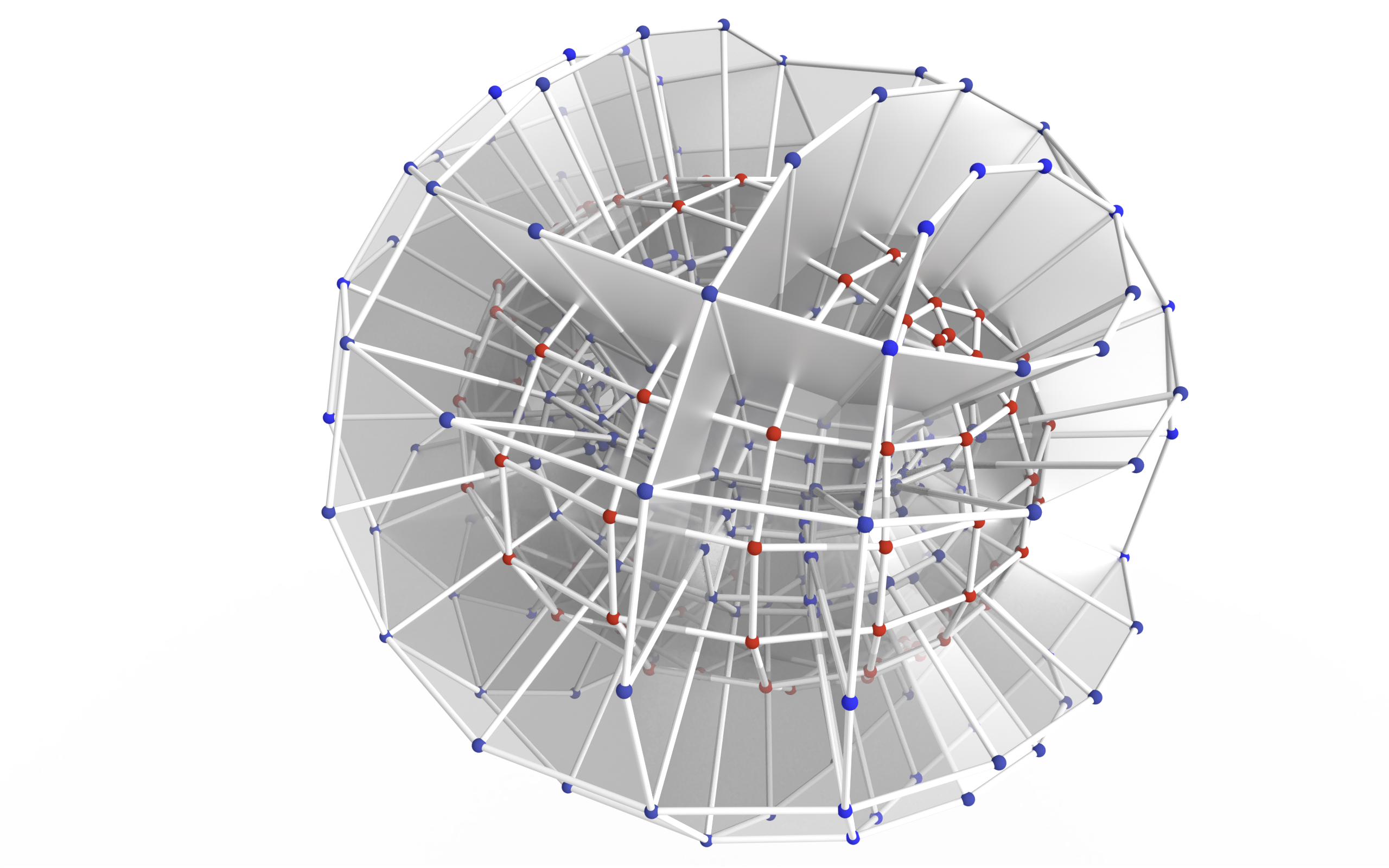
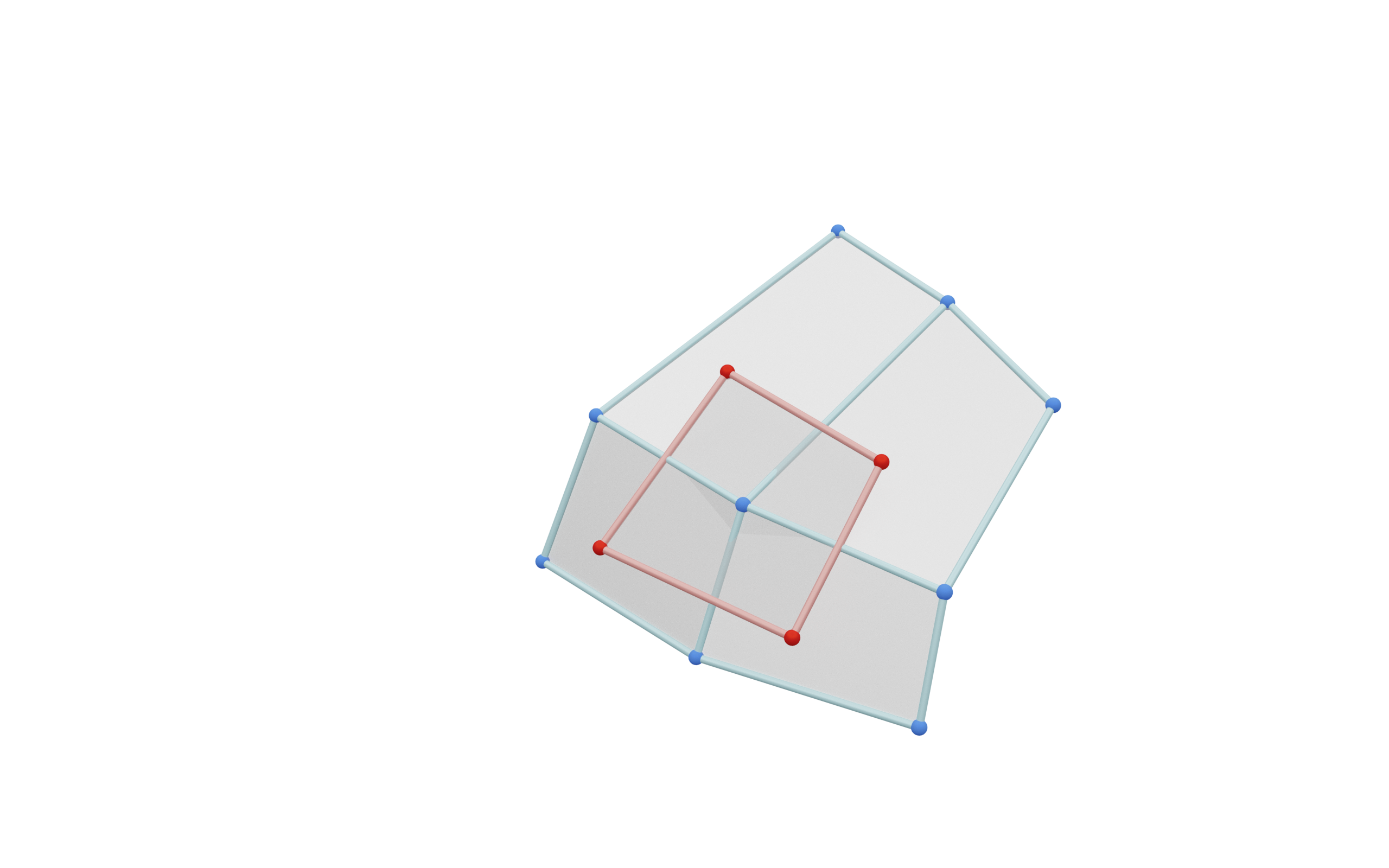
Principal Binets [AT24]



-
[BHS08] Minimal surfaces from circle patterns: Geometry from combinatorics
Bobenko, Hoffmann, Springborn.


-
[BHR19] Orthogonal ring patterns
Bobenko, Hoffmann, Rörig. -
[BHS24] Constant mean curvature surfaces from ring patterns: Geometry from combinatorics
Bobenko, Hoffmann, Smeenk.

-
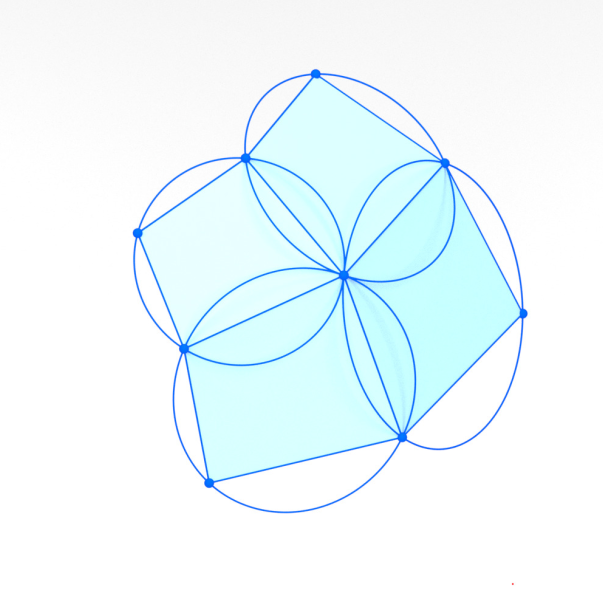
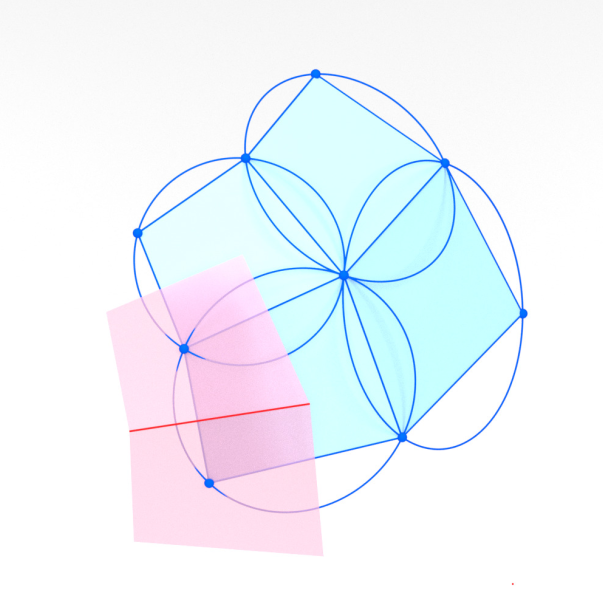
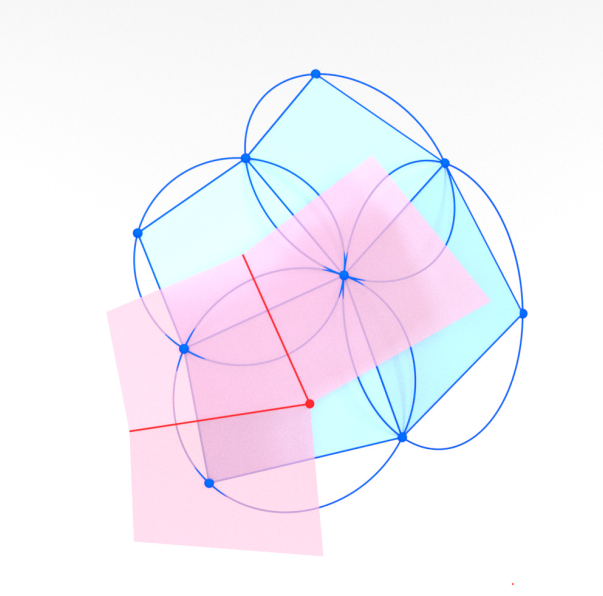
[BSST18] On a Discretization of Confocal Quadrics. A Geometric Approach to General Parametrizations
Bobenko, Suris, Schief, T. -
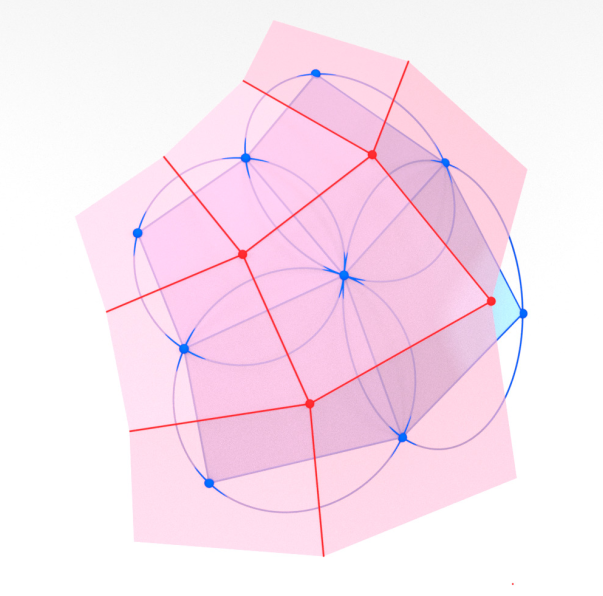
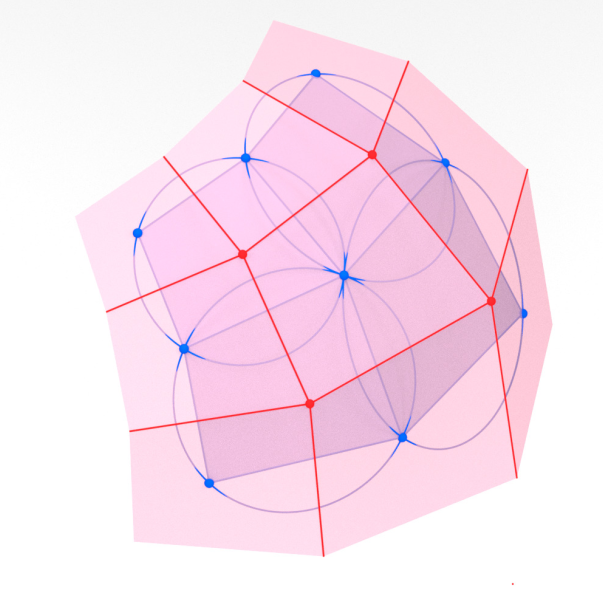
[HST25+]
A canonical discrete analogue of the classical circular cross sections of ellipsoids and their isometric deformation
Huang, Schief, T.

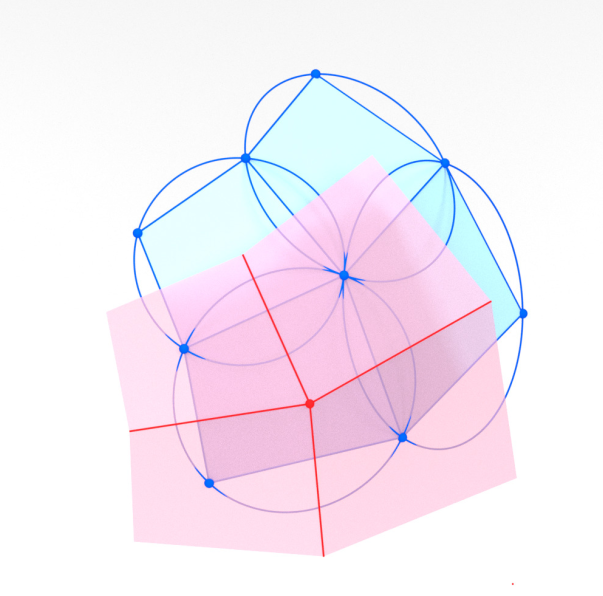
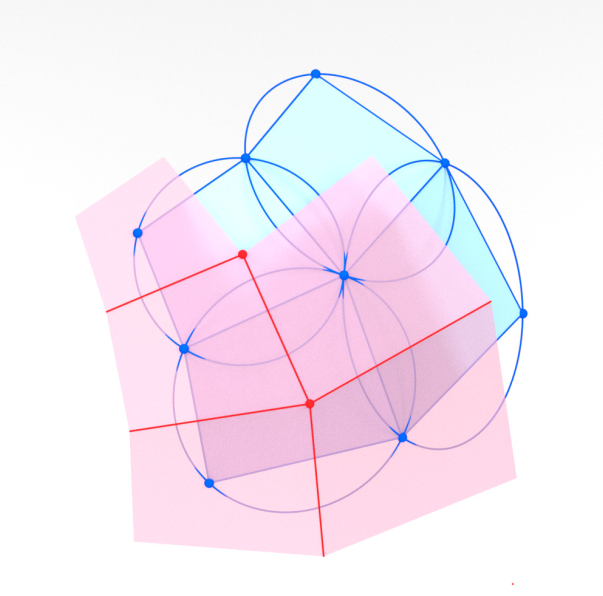
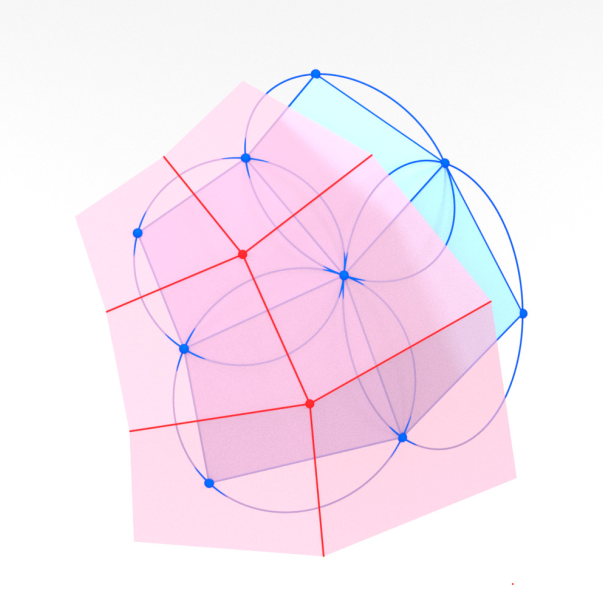
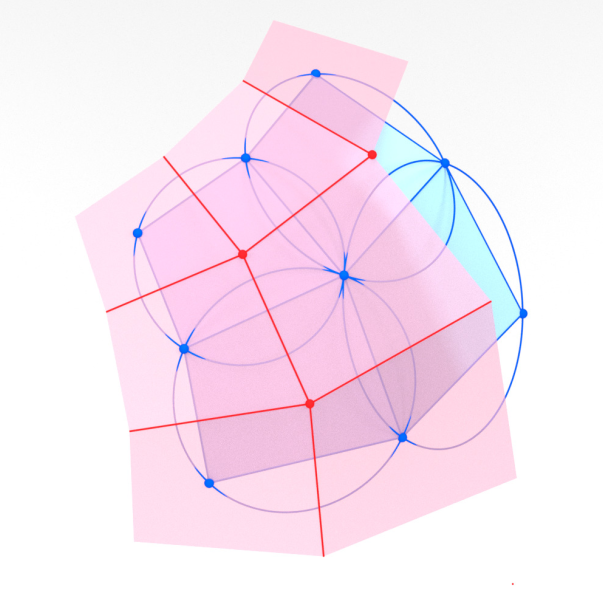
-
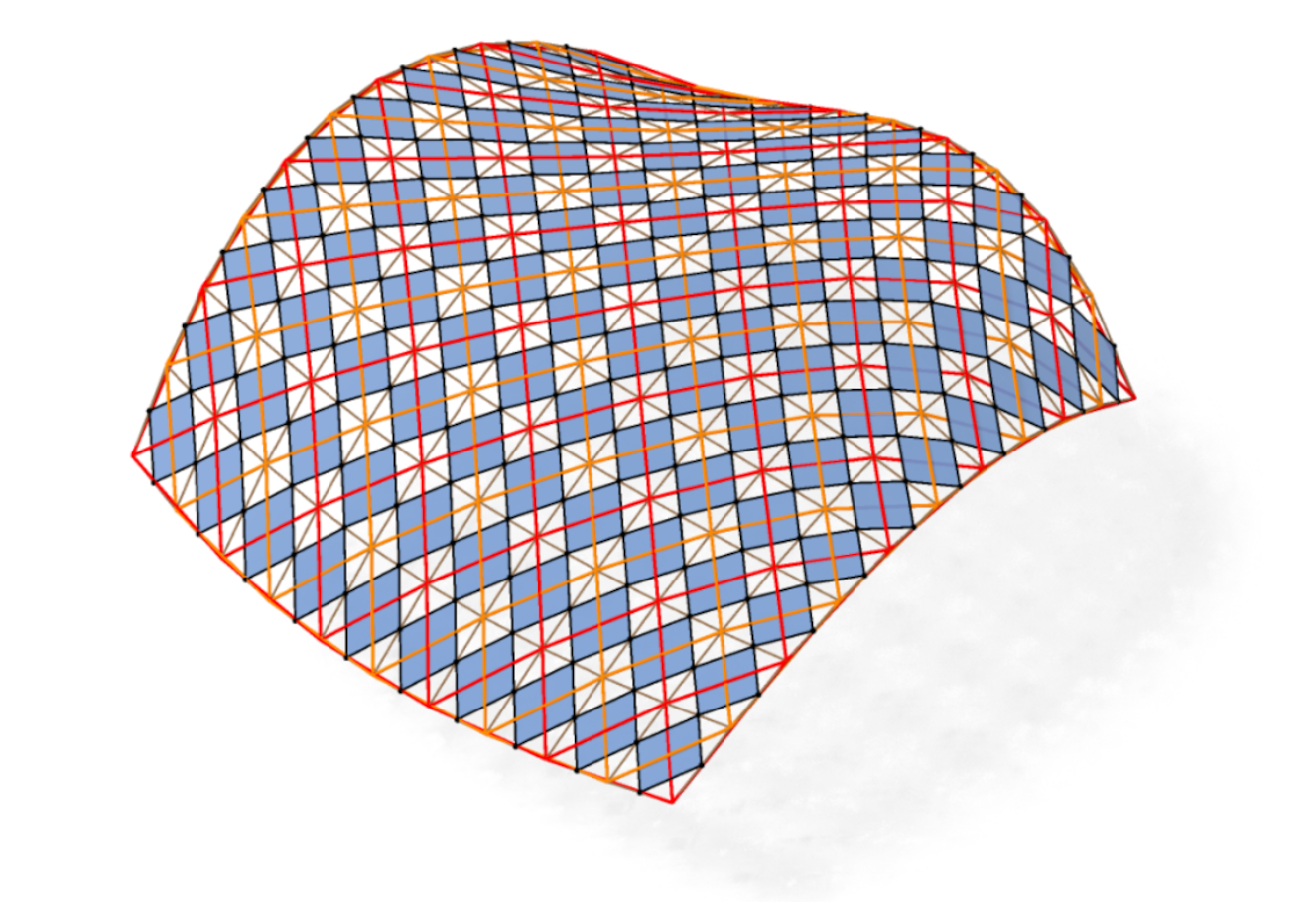
[BS07] On organizing principles of Discrete Differential Geometry. The geometry of spheres
Bobenko, Suris. -
[PW08] The focal geometry of circular and conical meshes
Pottmann, Wallner.

- [PJWP19] Checkerboard patterns with black rectangles
Peng, Jiang, Wonka, Pottmann. - [D22] Discrete Isothermic Nets Based on Checkerboard Patterns
Dellinger.
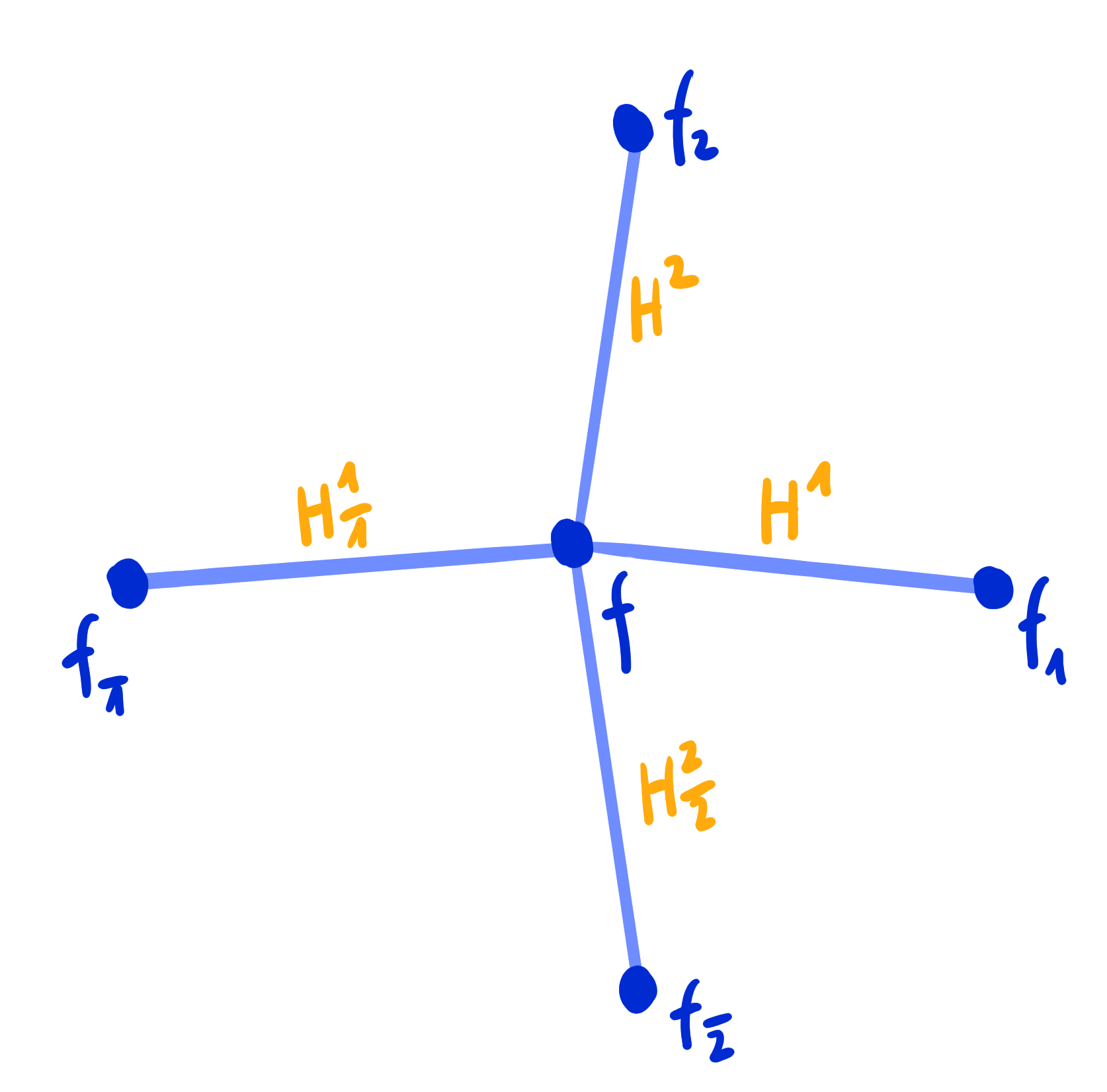
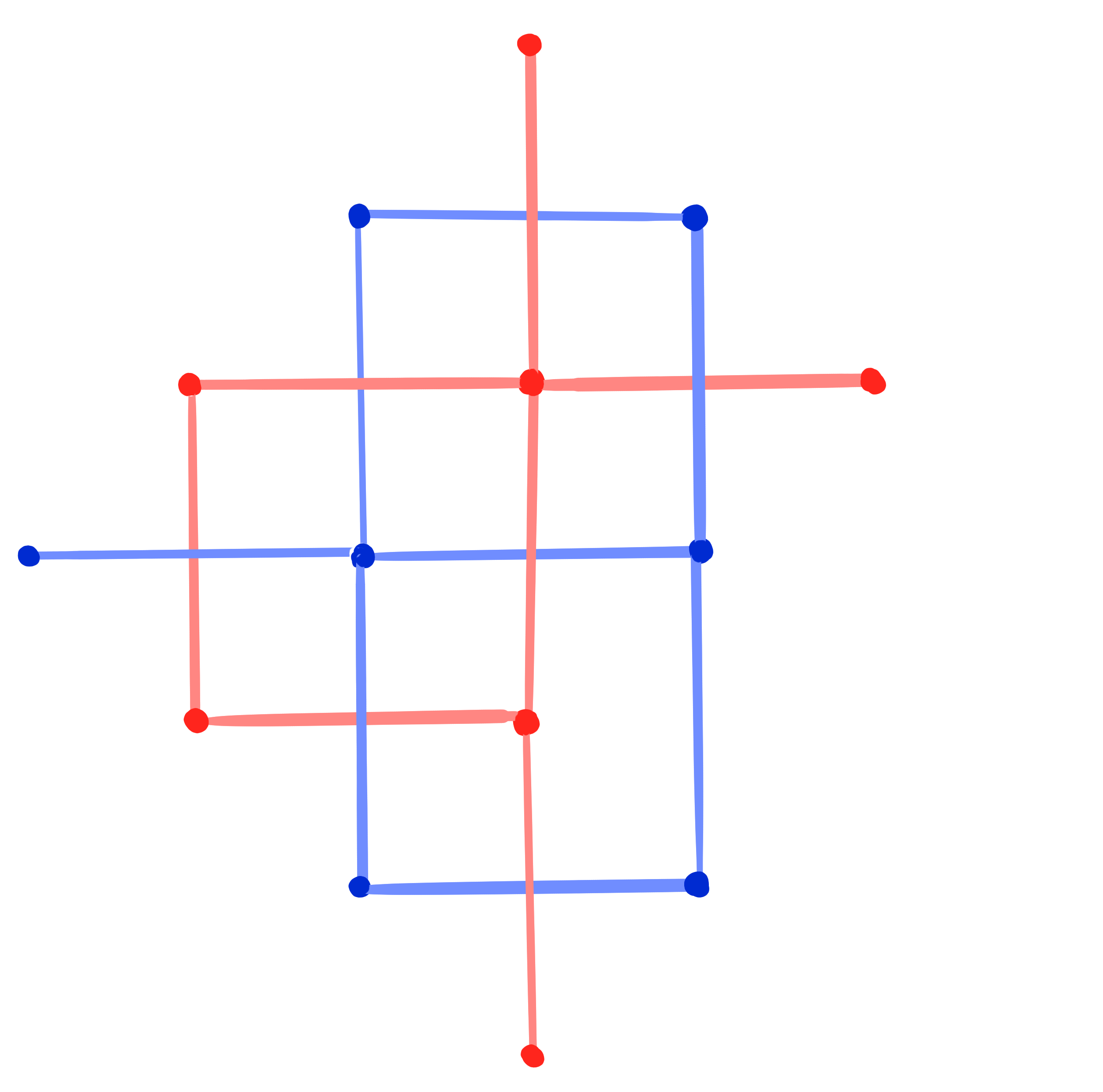
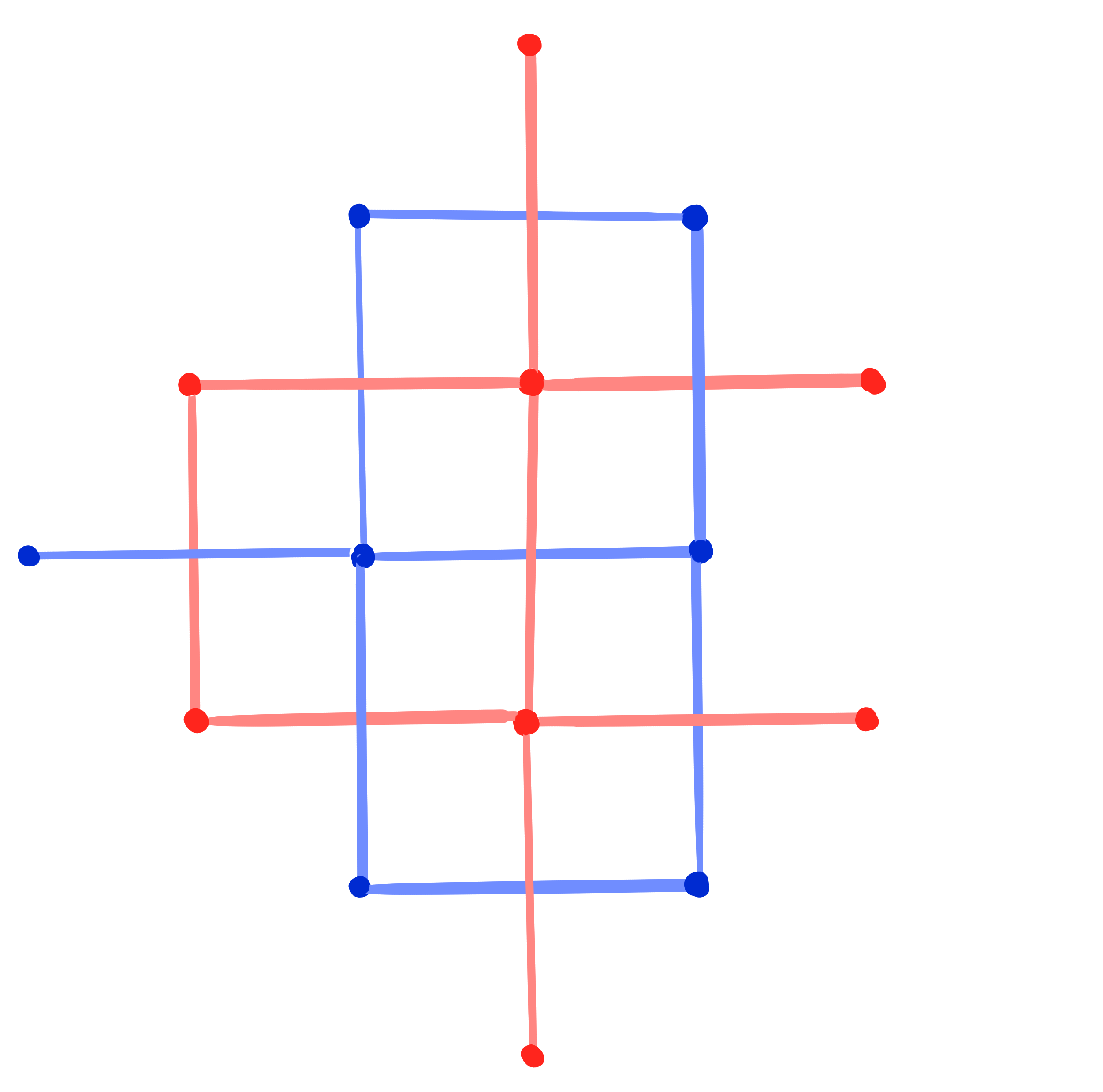
A ("classical" discrete) net is a map
$\Z^2 \rightarrow \R\mathrm{P}^n$.
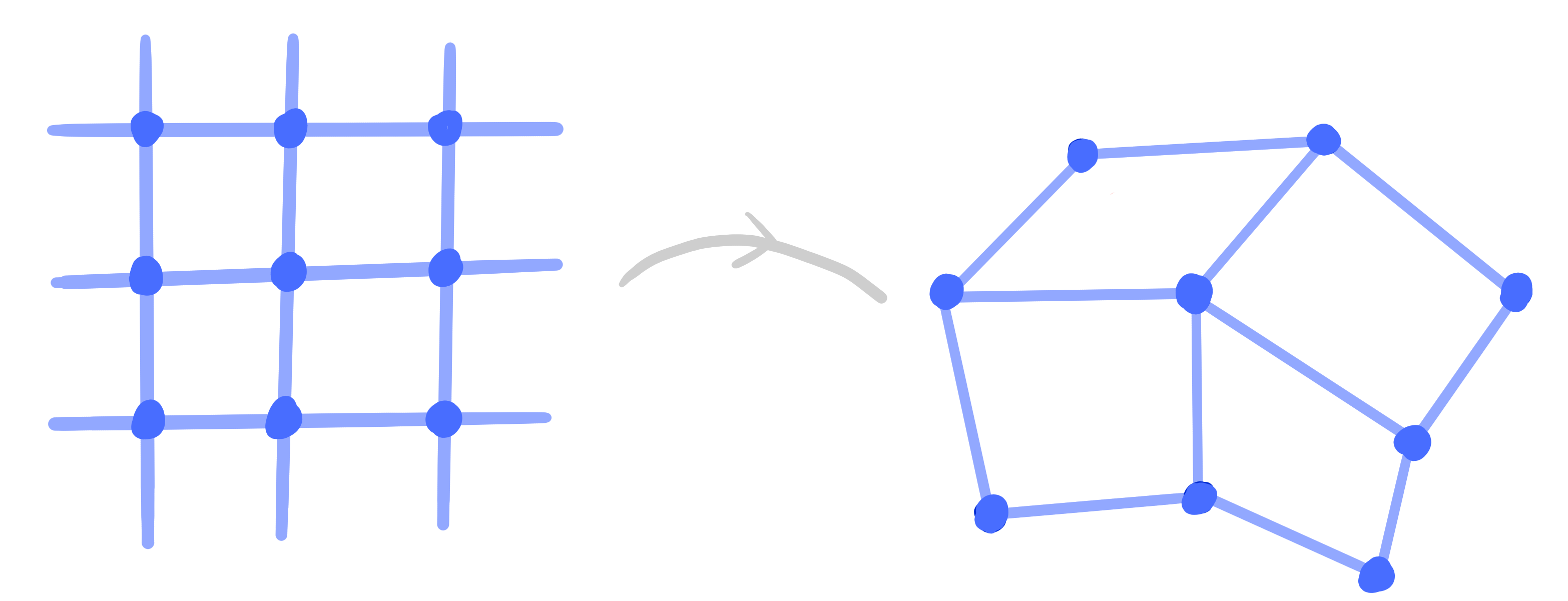
Definition:
A binet is a map
$\Z^2 \cup (\Z^2)^* \rightarrow \R\mathrm{P}^n$,
$(\Z^2)^* = F(\Z^2)$.
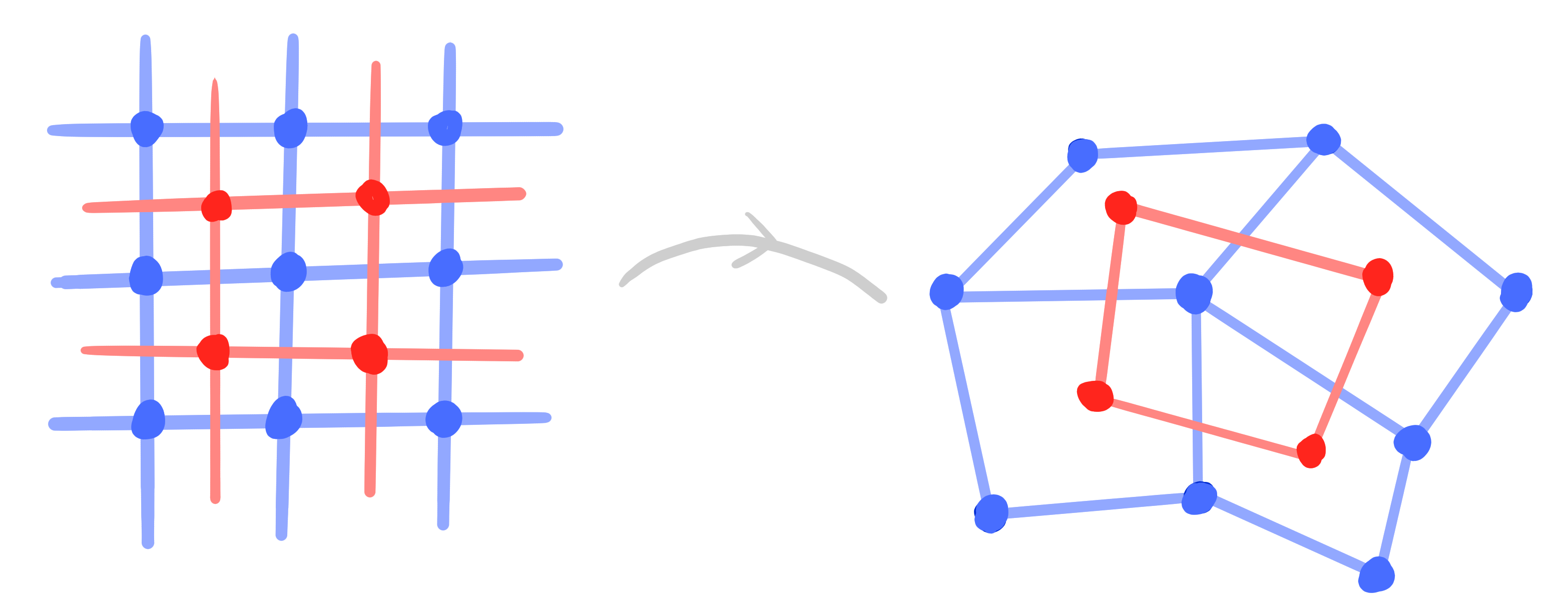
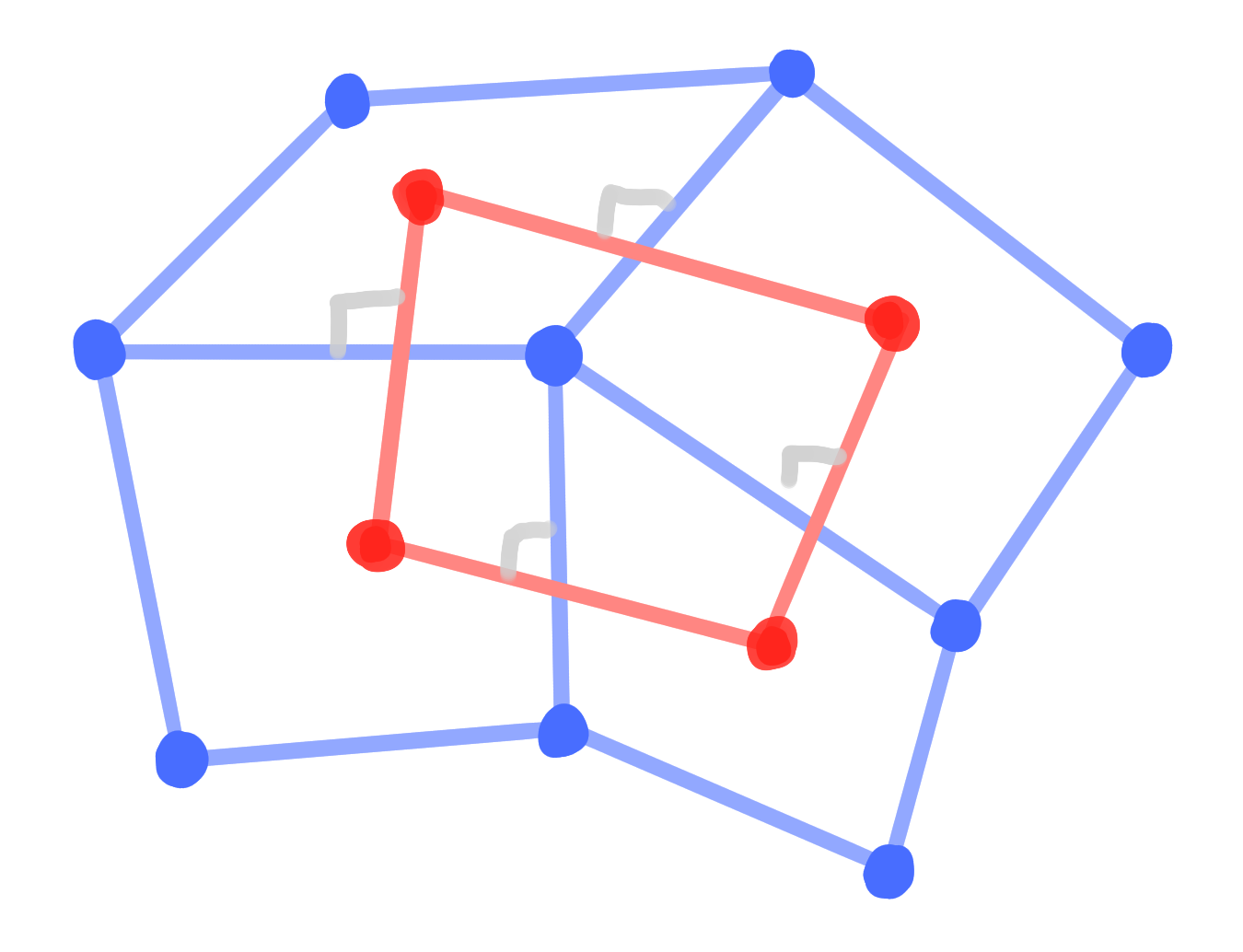
- vertices $V = V(\Z^2) = \Z^2$
- edges $E = E(\Z^2)$
- faces $F = F(\Z^2) = (\Z^2)^*$
- double graph $D = V \cup F$ ,$\qquad\qquad$ then a binet is a map $D \rightarrow \R\mathrm{P}^n$
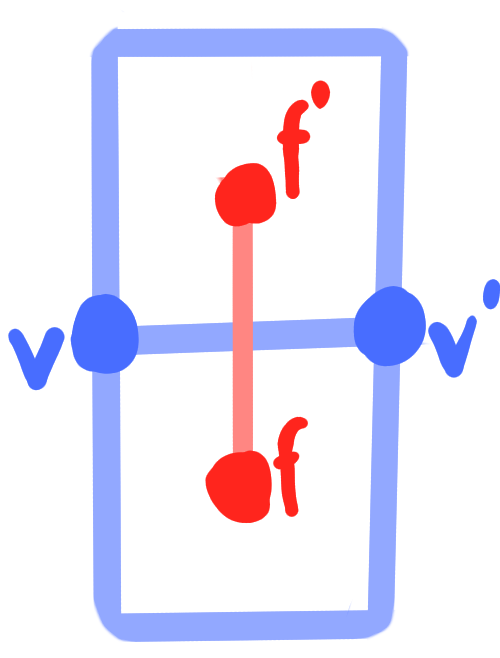
- crosses $C = \left\{ (v, f, v', f') ~|~ v,v'\in V,\quad f, f'\in F,\quad v, v' \text{ incident to } f, f' \right\}$
Smooth analogue:
Orthogonal parametrization (first fundamantal form diagonal).
Definition:
A binet $\quad b : D \rightarrow \R^3 \quad$ is called orthogonal
$\quad \Leftrightarrow \quad b(v) \vee b(v') \perp b(f) \vee b(f') \quad$ for all crosses $\quad (v, f, v', f') \in C$
$\quad \Leftrightarrow \quad b(v) \vee b(v') \perp b(f) \vee b(f') \quad$ for all crosses $\quad (v, f, v', f') \in C$
Invariances:
- independent translation of $b|_V$ and $b|_F$
- similarity transformations
- a priori, not Möbius invariant
Lemma:
Let $x_1, x_2, x_3, x_4 \in \R^3$.
Then there exist four spheres $S_1, S_2, S_3, S_4 \subset \R^3$ with these centers
and $S_1 \perp S_2 \perp S_3 \perp S_4 \perp S_1$
$\qquad \Leftrightarrow \quad x_1 x_3 \perp x_2 x_4$
Then there exist four spheres $S_1, S_2, S_3, S_4 \subset \R^3$ with these centers
and $S_1 \perp S_2 \perp S_3 \perp S_4 \perp S_1$
$\qquad \Leftrightarrow \quad x_1 x_3 \perp x_2 x_4$




Theorem:
Let $\quad b : D \rightarrow \R^3\quad$ be an orthogonal binet.
Then there exists a map $\quad S : D \rightarrow \left\{ \text{spheres in } \R^3\right\} \quad$ such that
Then there exists a map $\quad S : D \rightarrow \left\{ \text{spheres in } \R^3\right\} \quad$ such that
- for $d \in D$ the point $b(d)$ is the center of $S(d)$, and
- for incident $v \in V$ and $f \in F$: $\quad S(v) \perp S(f)$.

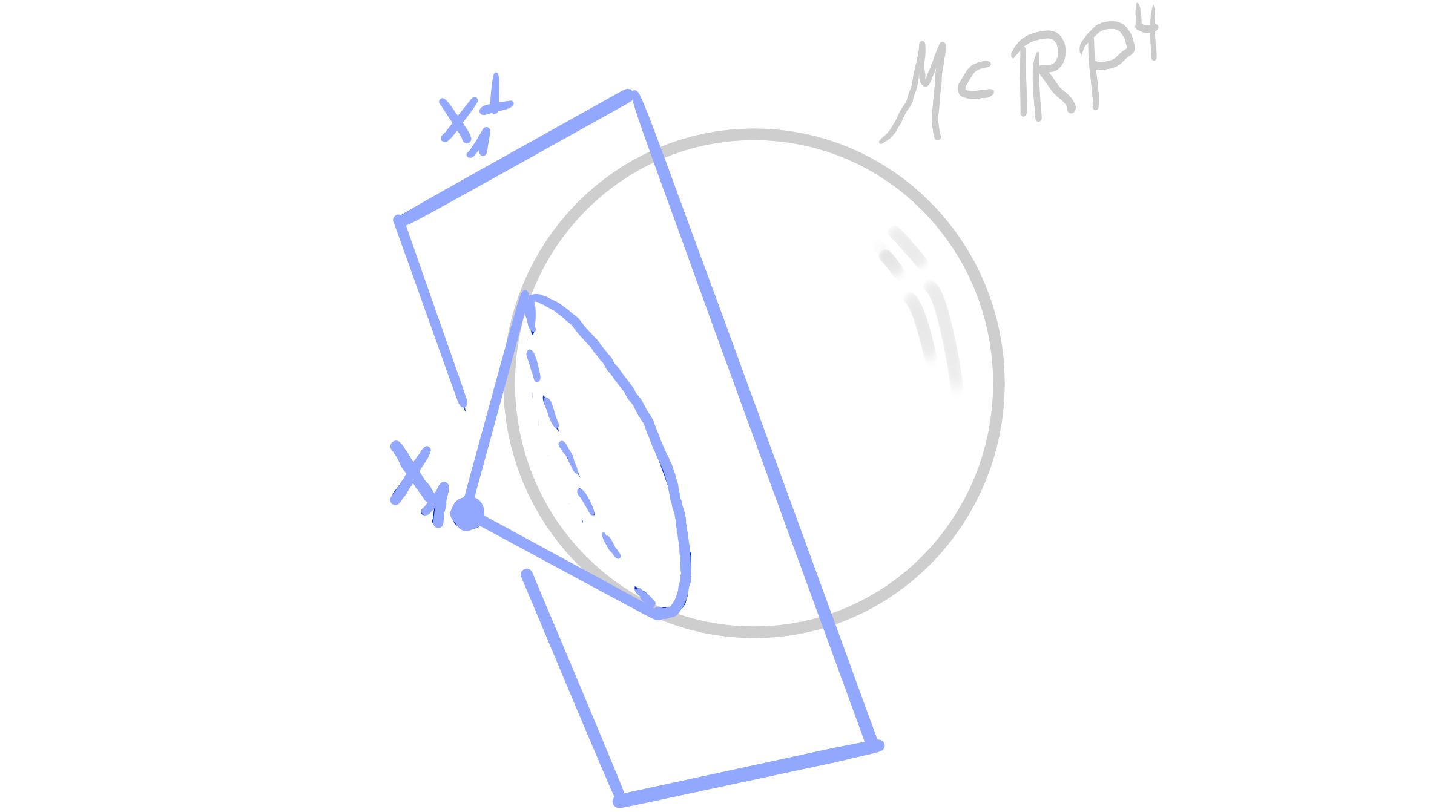
- The construction of $S$ has 1 degree of freedom (radius of one sphere).
- Orthogonal binets are Möbius invariant.
Orthogonal binets are Möbius invariant:
- Construct orthogonal sphere representation.
- Apply Möbius transformation to the spheres.
- Reconstruct centers.


|


|

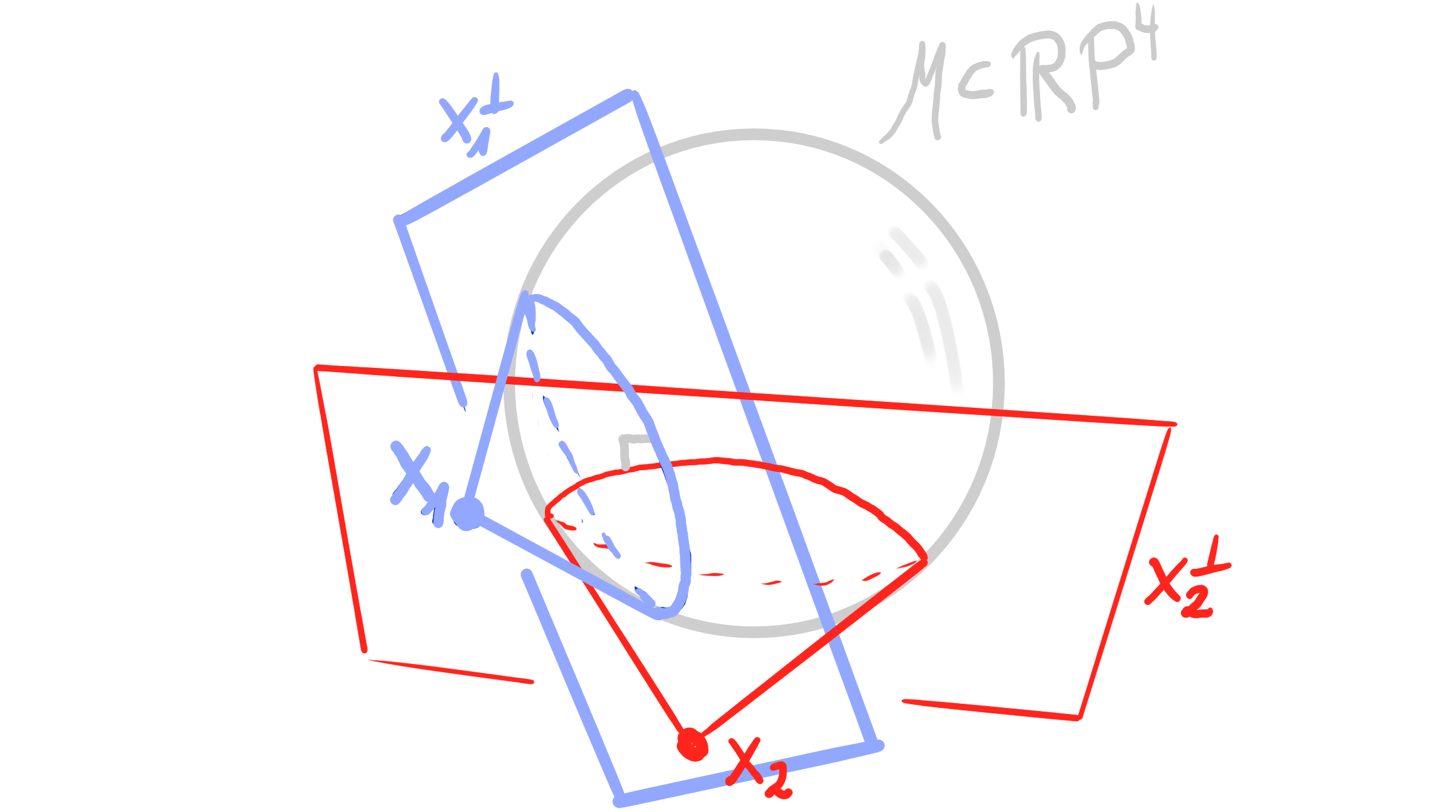
- a sphere $S \subset \mathcal{M}$ is represented by a point $\mathbf{x} \in \R\mathrm{P}^4$ via polarity: $\qquad S = \mathbf{x}^\perp \cap \mathcal{M}$
- $ S_1 \perp S_2 \quad \Leftrightarrow \quad \mathbf{x}_1 \perp \mathbf{x}_2 \quad \Leftrightarrow \quad \langle x_1, x_2 \rangle_{\mathcal{M}} = 0 $
|
Theorem:
Let $~ b : D \rightarrow \R^3\,$ be an orthogonal binet. Then there exists a lift $~b_{\mathcal{M}} : D \rightarrow \R P^4$ such that \[ \begin{aligned} &\pi_{\mathbf{B}} \circ b_{\mathcal{M}}= b\\ &b_{\mathcal{M}}(v) \perp b_{\mathcal{M}}(f) \end{aligned} \] |
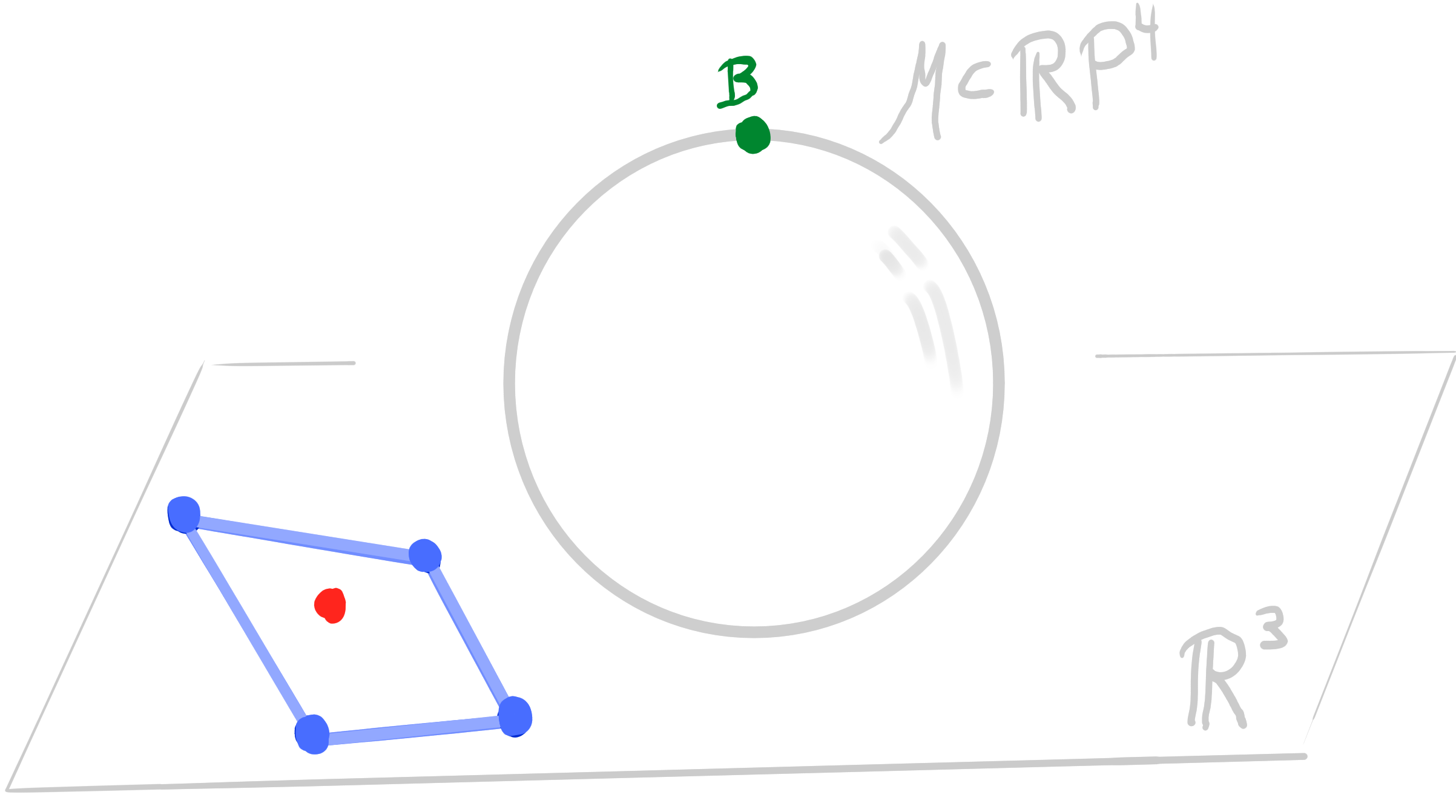
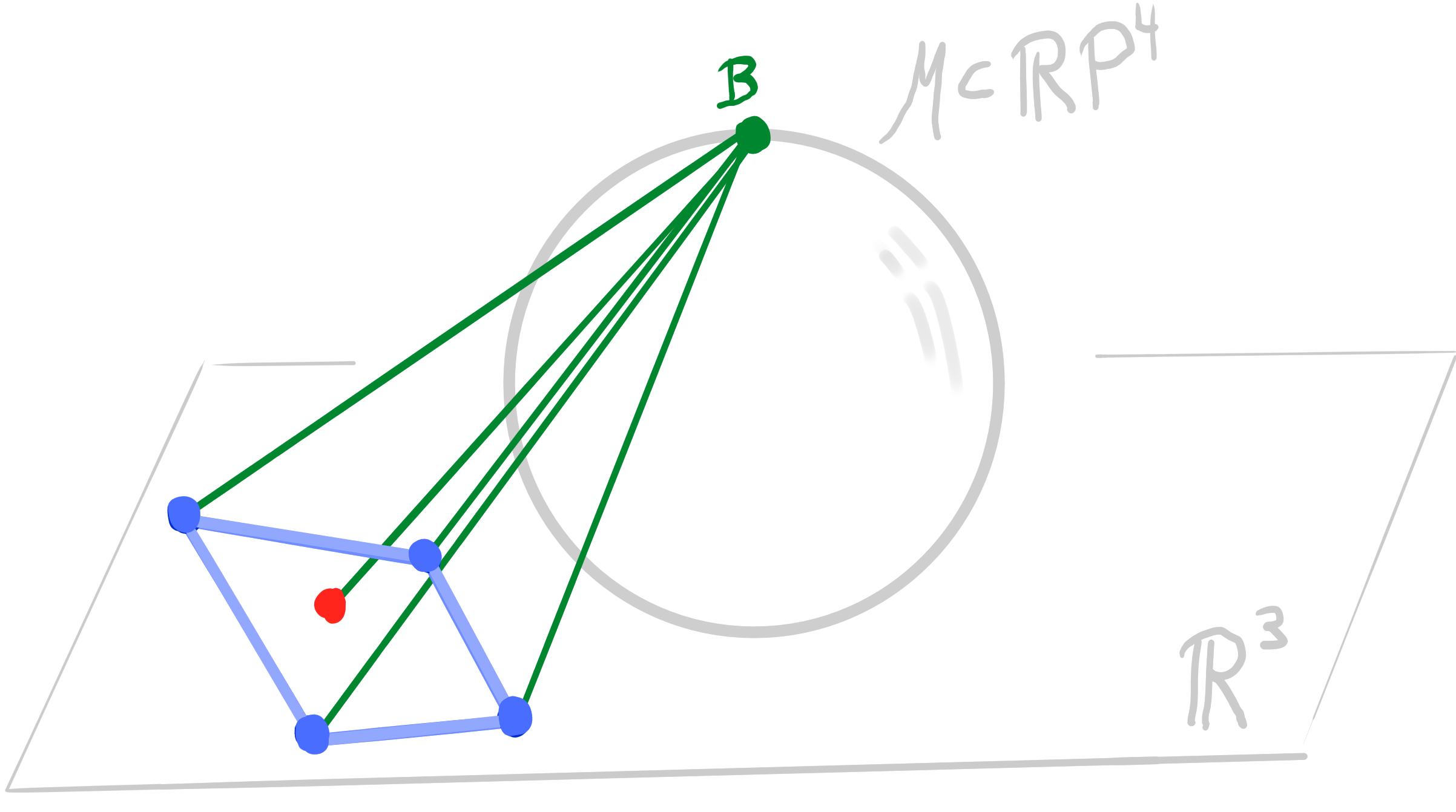
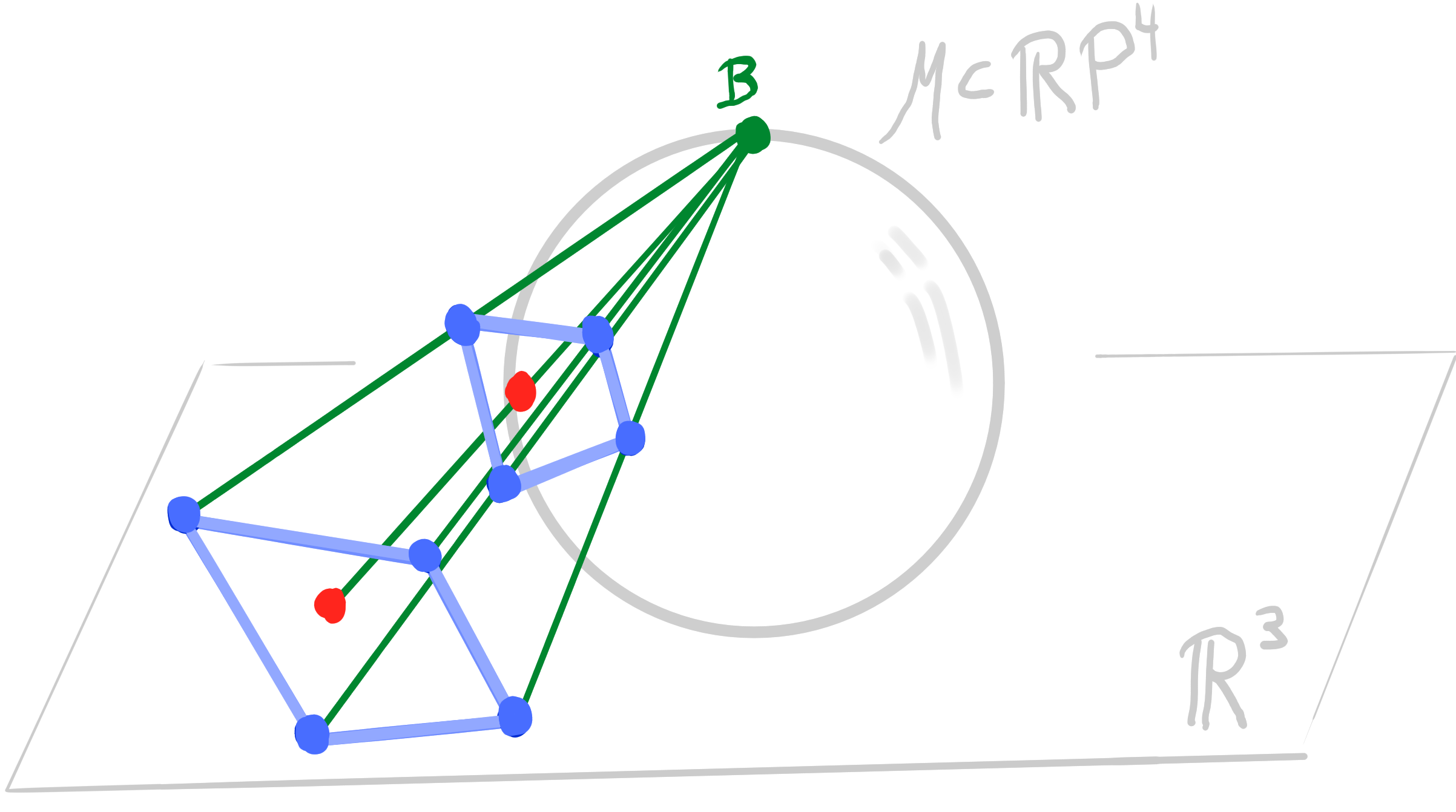
|
- Orthogonality in $\R^3$ becomes polarity in $\R\mathrm{P}^4$ in the lift.
- The Möbius lift has 1 degree of freedom (radius of one sphere).
Definition:
Let $\mathcal{Q} \subset \R\mathrm{P}^n$ be a quadric.
A polar binet is a map $~ b : D \rightarrow \R\mathrm{P}^n ~$ such that
for any two incident $v \in V$ and $f \in F$ the two points $b(v)$ and $b(f)$ are polar: \[ b(v) \perp b(f) \]
Let $\mathcal{Q} \subset \R\mathrm{P}^n$ be a quadric.
A polar binet is a map $~ b : D \rightarrow \R\mathrm{P}^n ~$ such that
for any two incident $v \in V$ and $f \in F$ the two points $b(v)$ and $b(f)$ are polar: \[ b(v) \perp b(f) \]
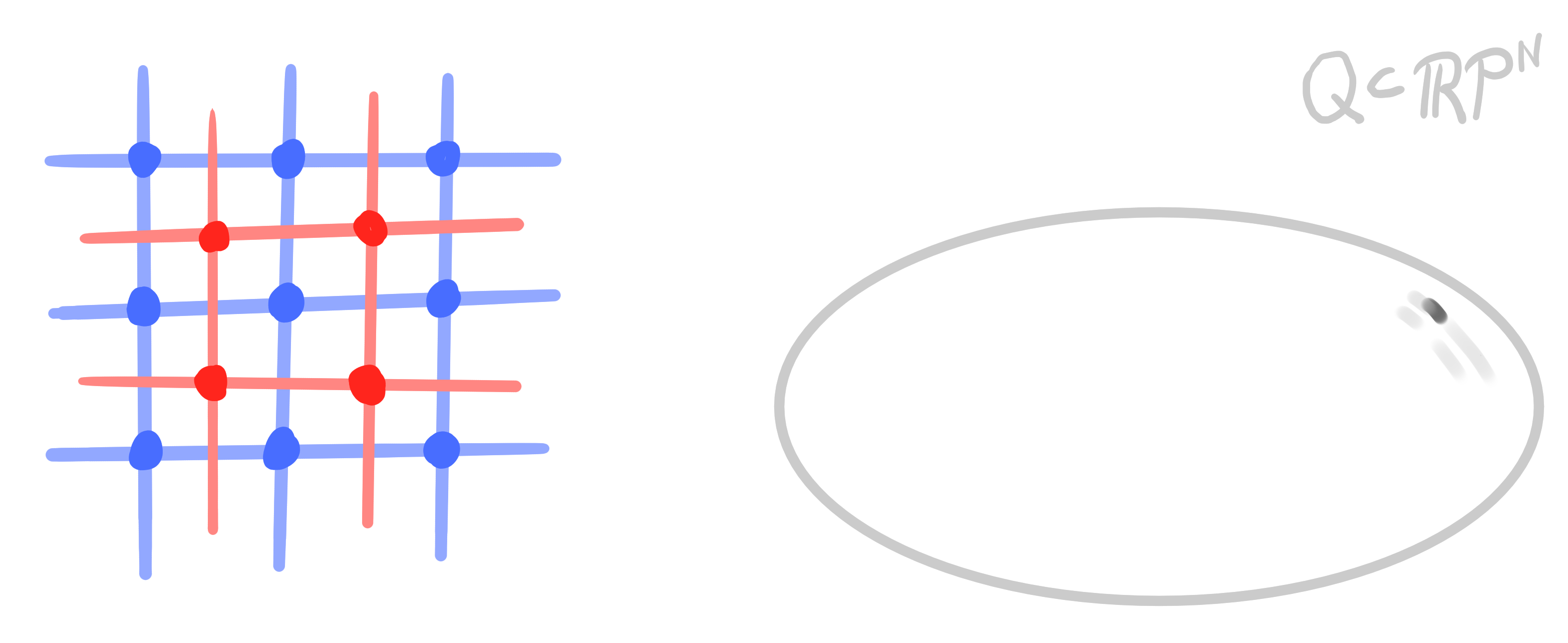
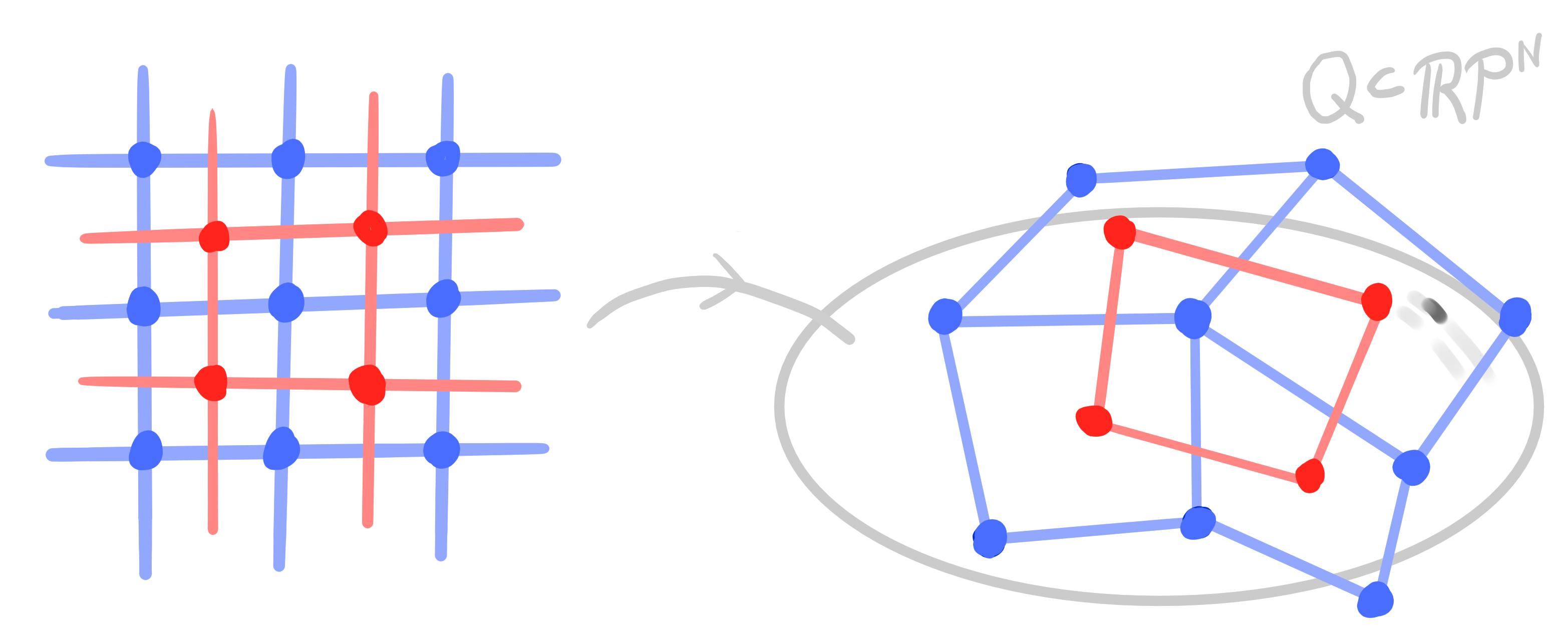
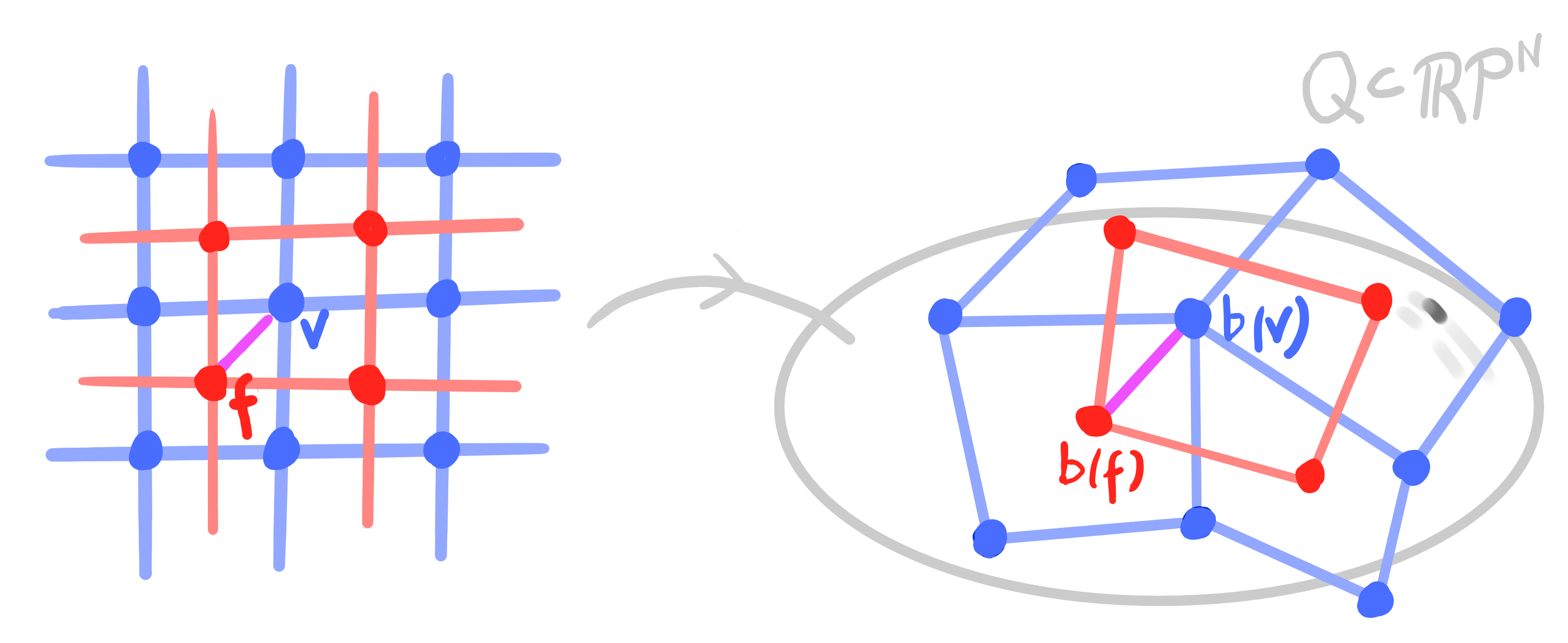
Conclusion:
Orthogonal binets in $\R^3$ can be lifted to polar binets in $\R\mathrm{P}^4$.
Vice versa, polar binets in $\R\mathrm{P}^4$ project to orthogonal binets in $\R^3$.
Orthogonal binets in $\R^3$ can be lifted to polar binets in $\R\mathrm{P}^4$.
Vice versa, polar binets in $\R\mathrm{P}^4$ project to orthogonal binets in $\R^3$.
|
Smooth analogue:
Conjugate parametrization
(second fundamantal form diagonal). |
|
|
Definition: A binet $~ b : D \rightarrow \R^3 ~$ is called conjugate $\Leftrightarrow$ $b|_V$ and $b|_F$ have planar faces (Q-nets) |
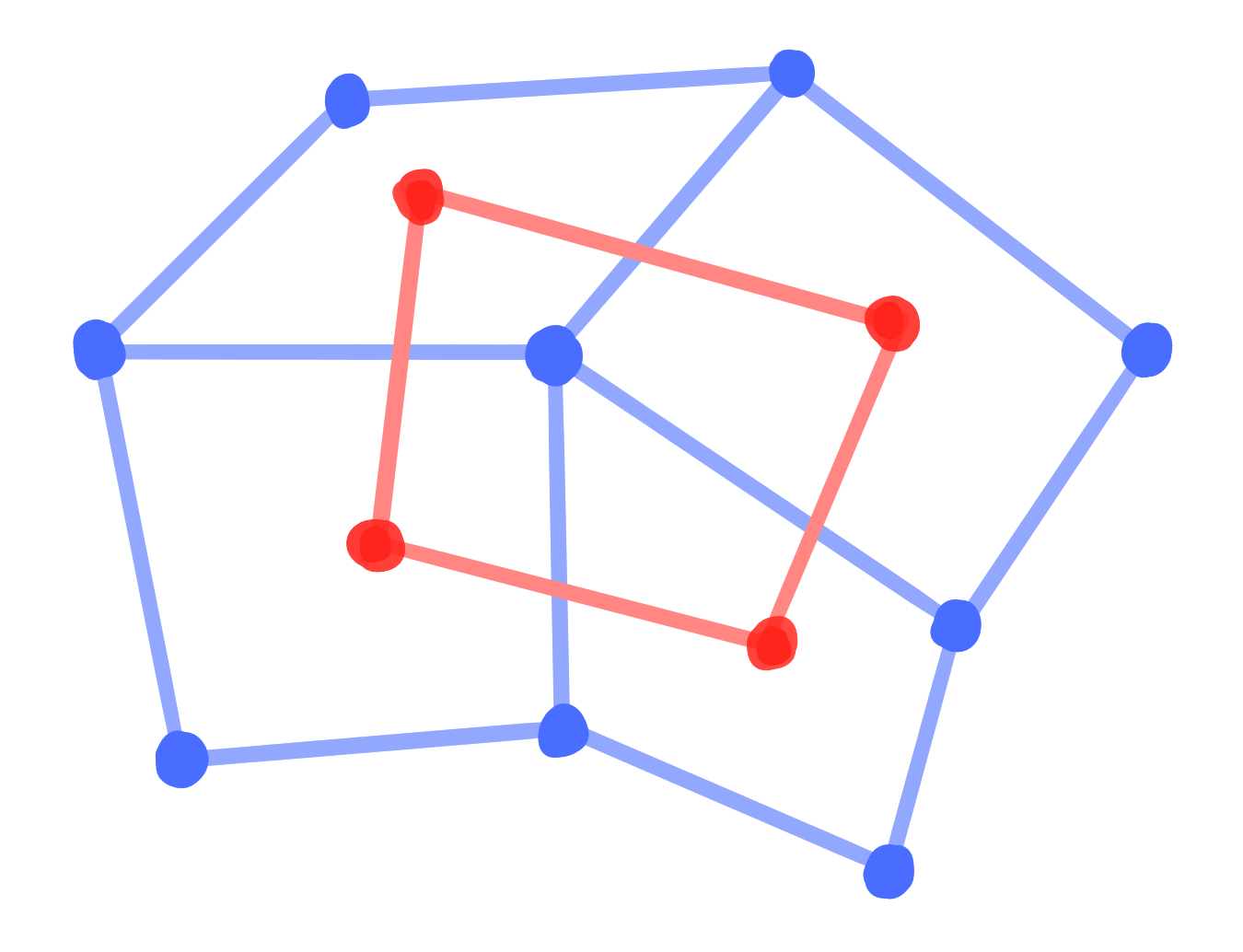
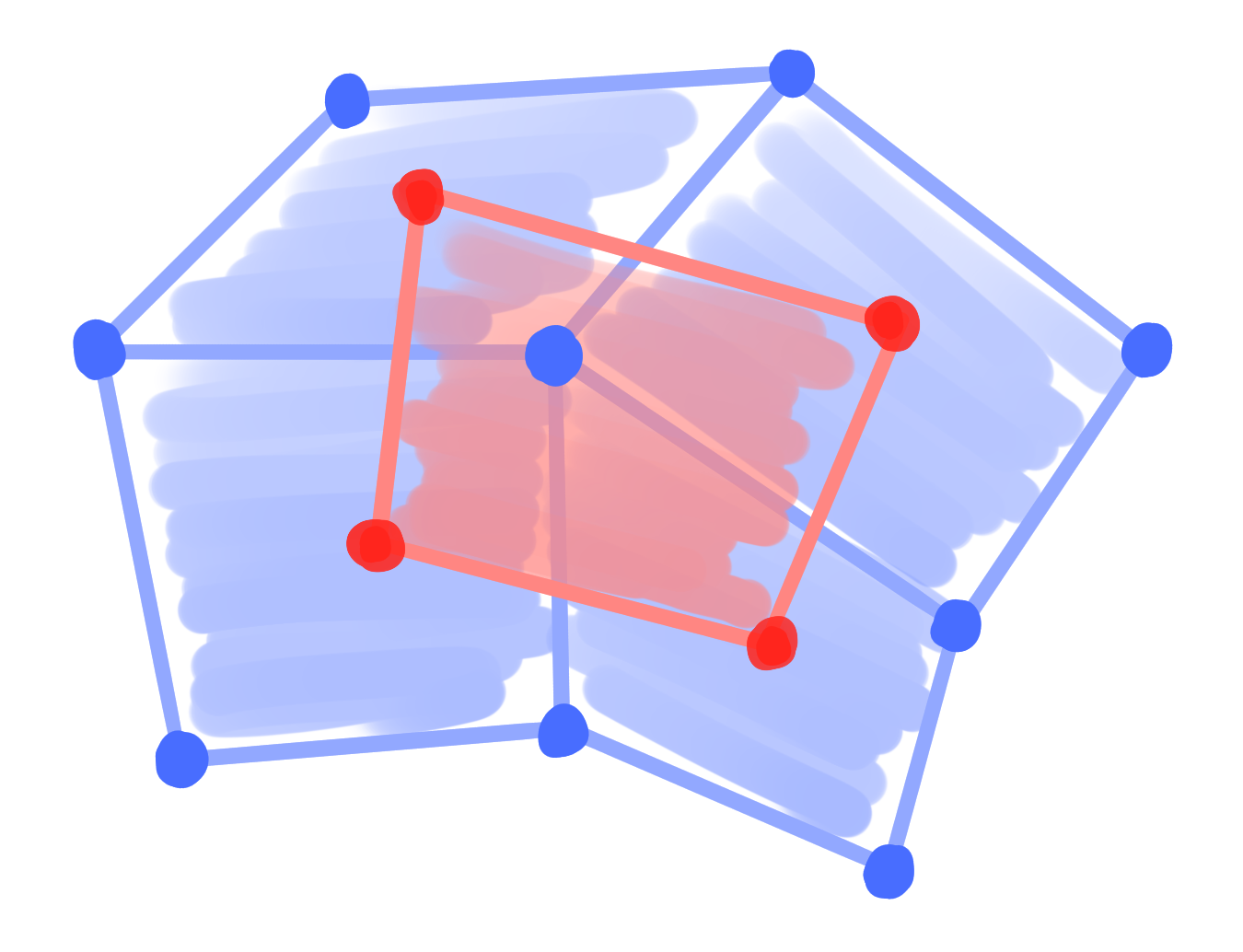
|
Smooth analogue:
Principal parametrization / curvature line parametrization
(first and second fundamental form diagonal).
(first and second fundamental form diagonal).
Definition:
A principal binet $~ b : D \rightarrow \R^3 ~$ is a binet that is both conjugate and orthogonal.
A principal binet $~ b : D \rightarrow \R^3 ~$ is a binet that is both conjugate and orthogonal.
Theorem:
Let $~b : D \rightarrow \R^3~$ be a principal binet.
Then its Möbius lift $~b_\mathcal{M} : D \rightarrow \R\mathrm{P}^4~$ is a conjugate polar binet.
Let $~b : D \rightarrow \R^3~$ be a principal binet.
Then its Möbius lift $~b_\mathcal{M} : D \rightarrow \R\mathrm{P}^4~$ is a conjugate polar binet.
-
Additional structure induced by planar sections of the Möbius quadric:
Circle per $d \in D$.
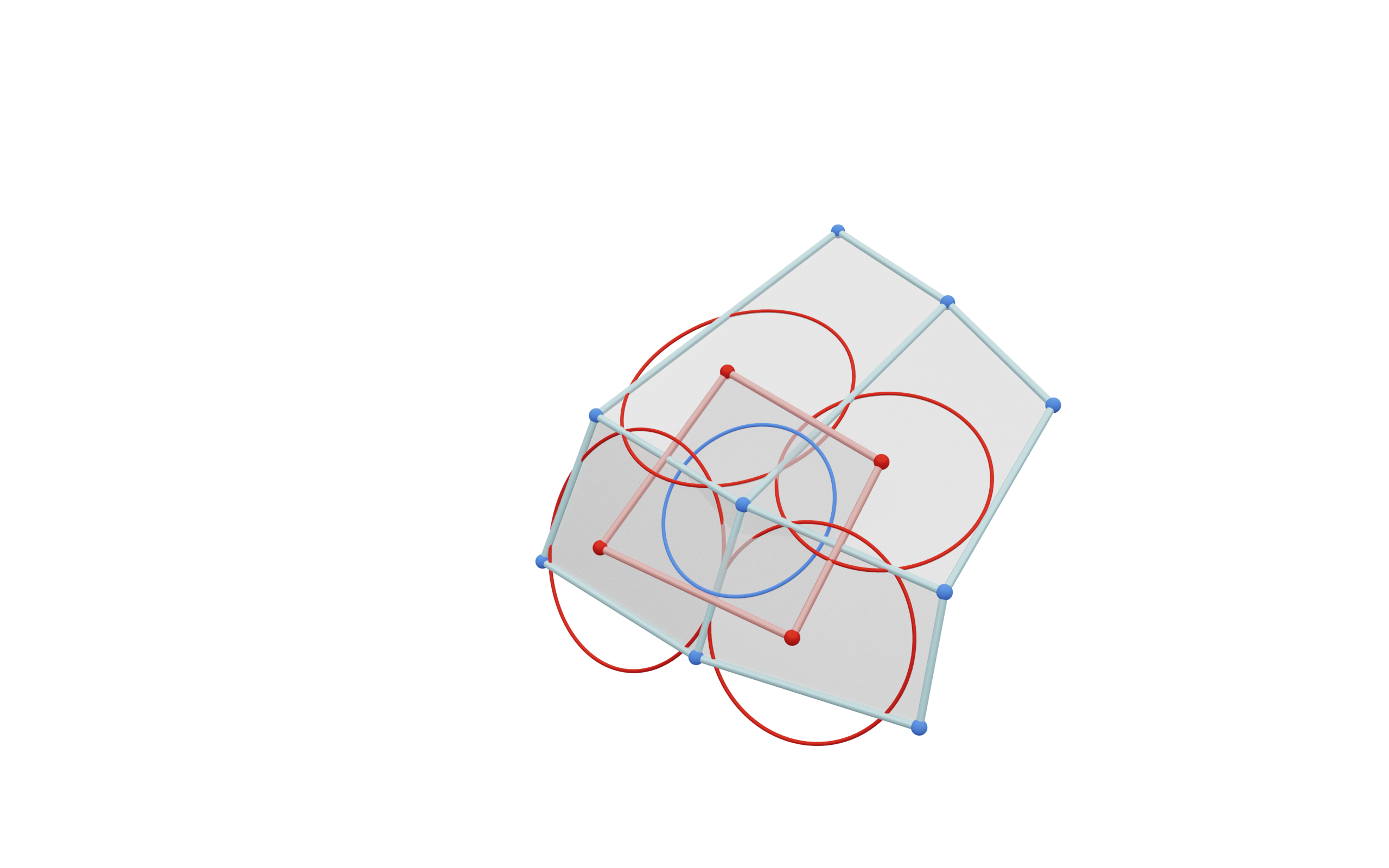

- Generalize the circles of circular nets.
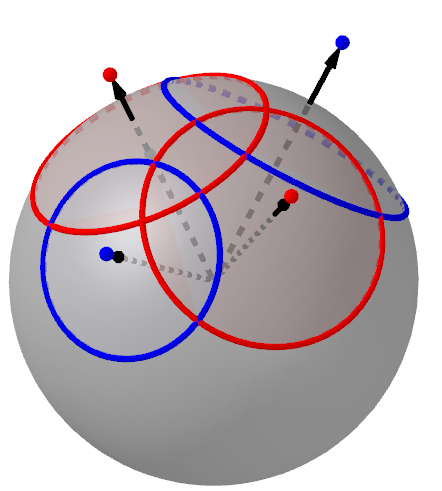
Definition of curvature spheres on edges as common sphere of adjacent circles.
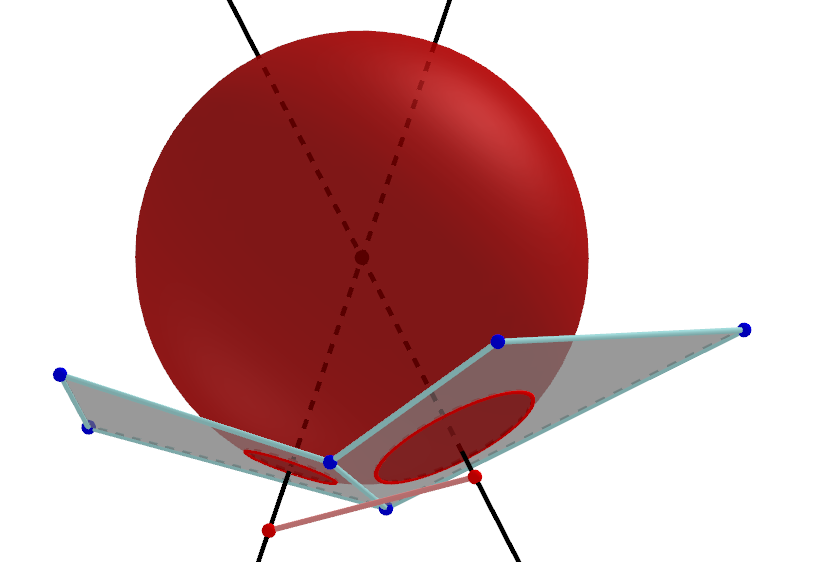
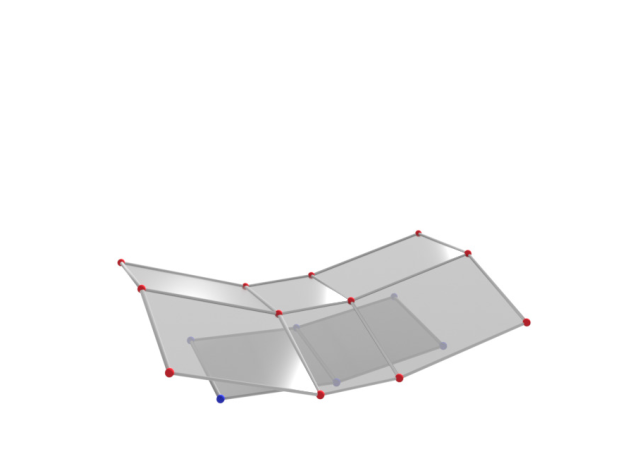
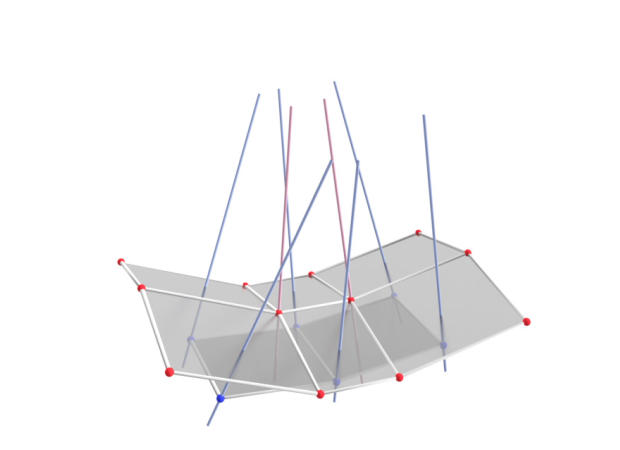
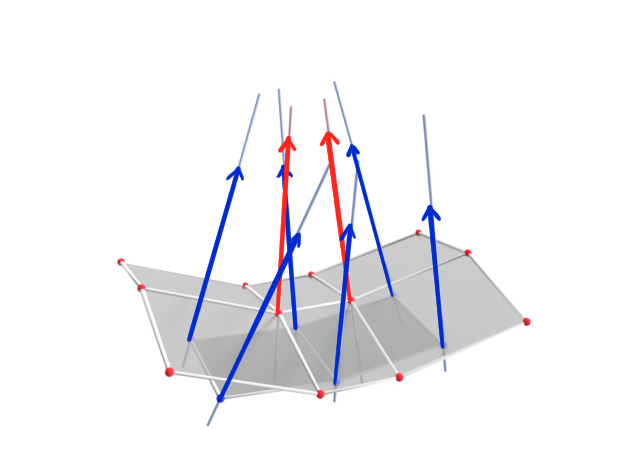
Theorem :
Let $\, b : D \rightarrow \R^3 \,$ be a principal binet.
Then there exists a map $\, n : D \rightarrow \R^3 \,$, called normal binet of $b$, such that
Then there exists a map $\, n : D \rightarrow \R^3 \,$, called normal binet of $b$, such that
- for any $d \in D$: $\quad n(d)$ normal vector of $\square b(d)$,
- for incident $v \in V$ and $f \in F$: $\quad \langle n(v), n(f) \rangle = 1$.
|
|
- The construction of $n$ has 1 degree of freedom (length of one normal vector).
- Adjacent normal lines intersect ($\rightarrow$ focal nets and parallel nets)
- Corresponding edges of $n$ and $b$ are parallel ($\rightarrow$ curvatures from Steiner formula).
- Gives rise to an orthogonal circle representation on the sphere.
Definition of Laguerre lift of a principal binet
by combining its planes and normal binet into angled planes.
by combining its planes and normal binet into angled planes.

- Principal binets are Laguerre invariant.
-
Normal binet and Laguerre lift exist for general orthogonal bi*nets
(smooth analogue: third fundamental form diagonal)
Theorem:
Let $~b : D \rightarrow \mathbb{R}^3$ be a principal binet.
Then its Laguerre lift $~b_\mathcal{B} : D \rightarrow \R\mathrm{P}^4~$ is a conjugate polar binet.
Let $~b : D \rightarrow \mathbb{R}^3$ be a principal binet.
Then its Laguerre lift $~b_\mathcal{B} : D \rightarrow \R\mathrm{P}^4~$ is a conjugate polar binet.
-
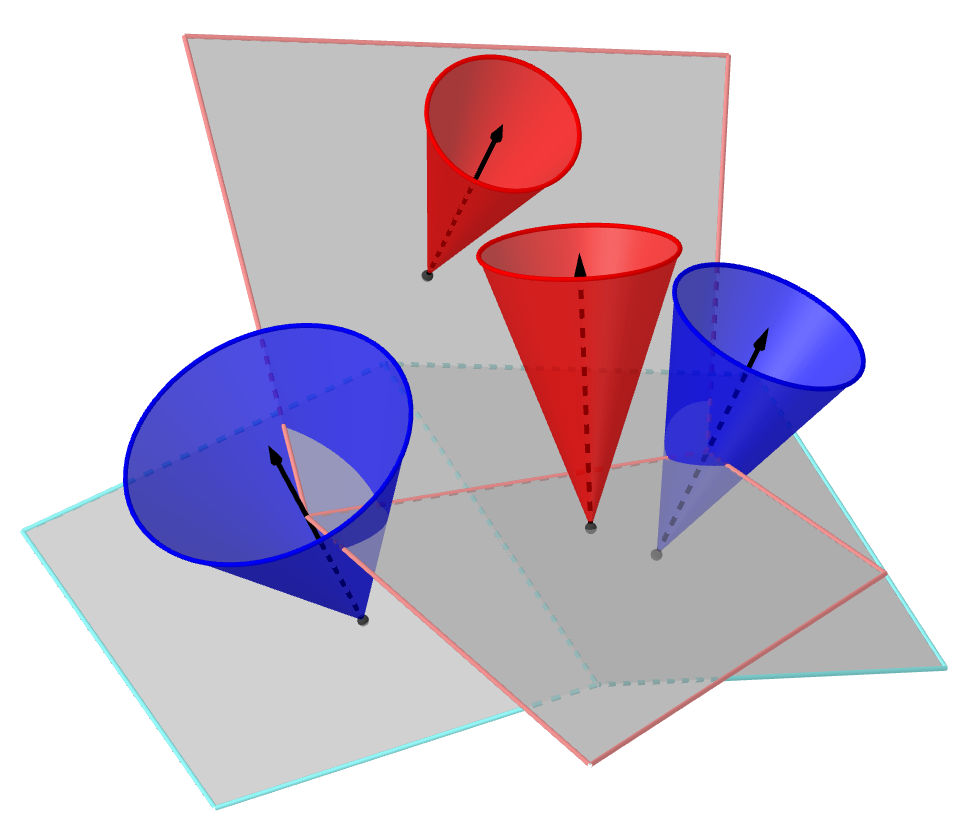
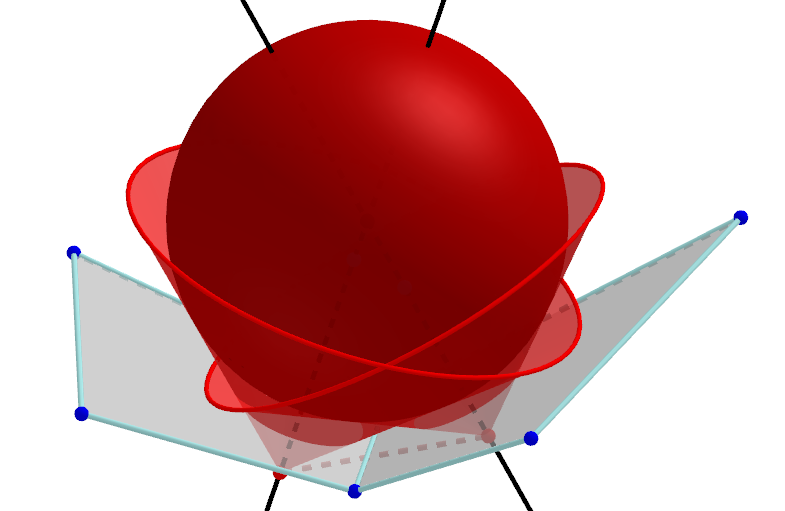
Additional structure induced by planar sections of the Blaschke cylinder:
Cone per $d \in D$.
|

|
- Generalizes the cones of conical nets.
Definition of Laguerre curvature spheres on edges as common sphere of adjacent cones.
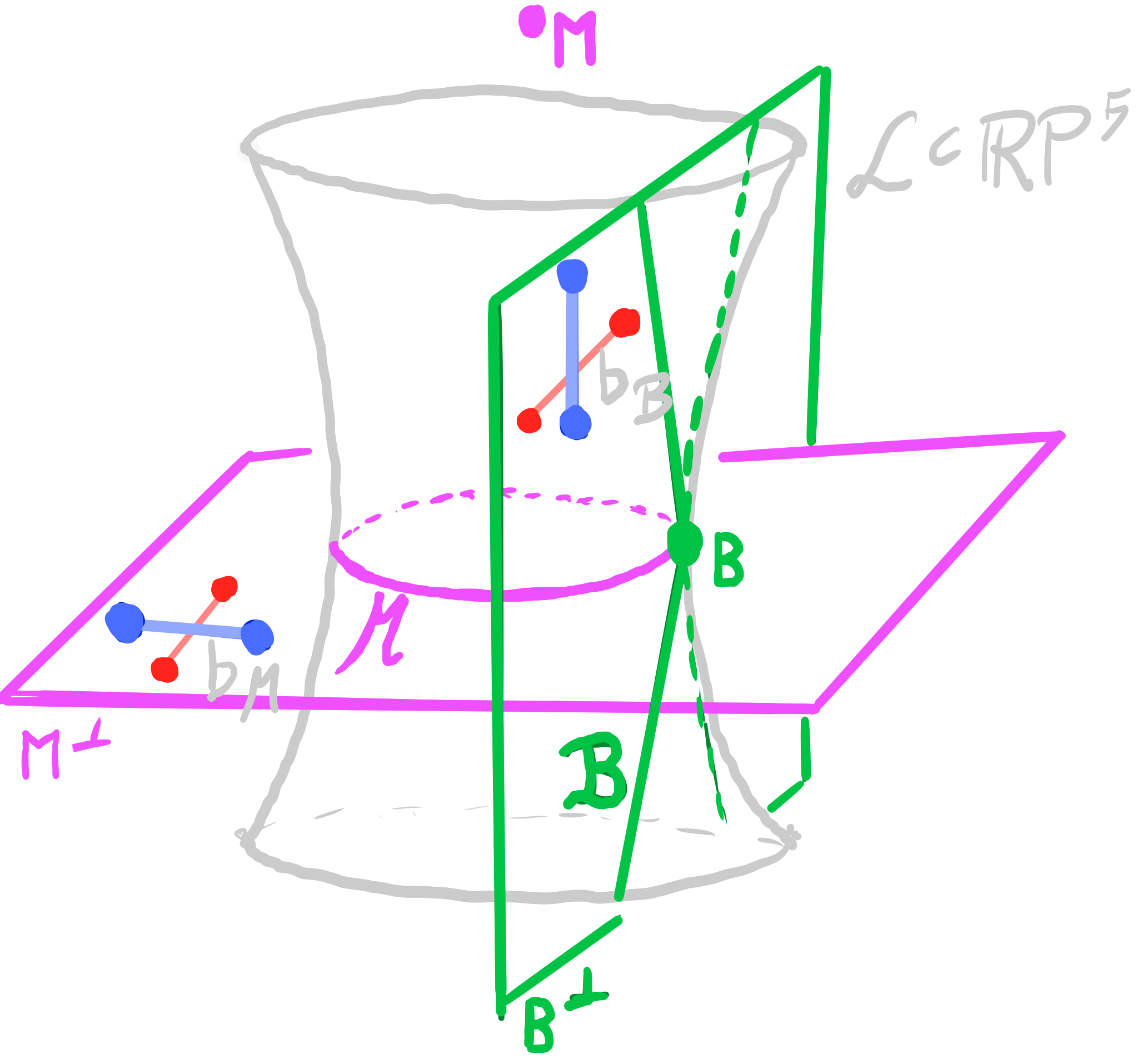
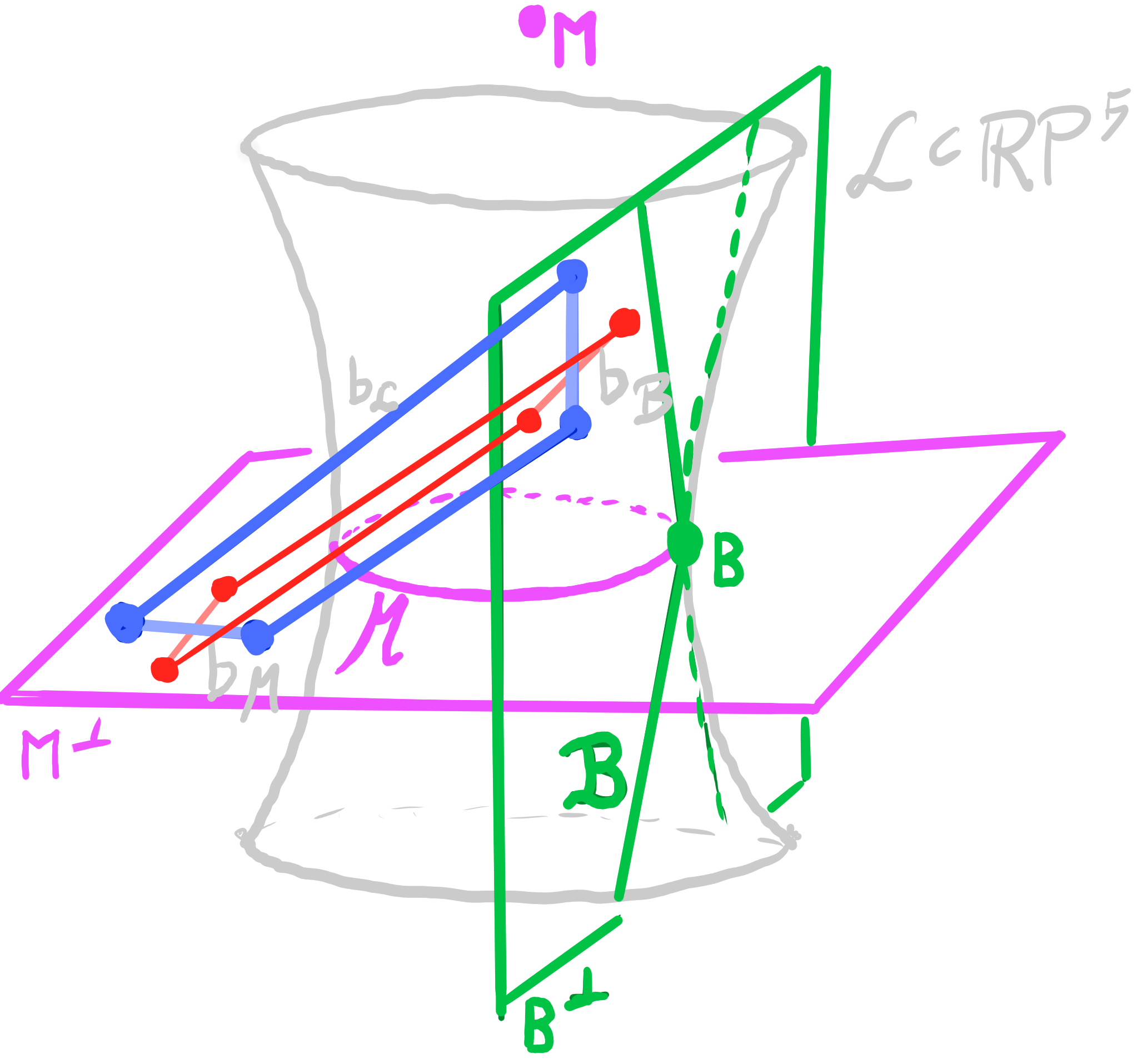
Definition:
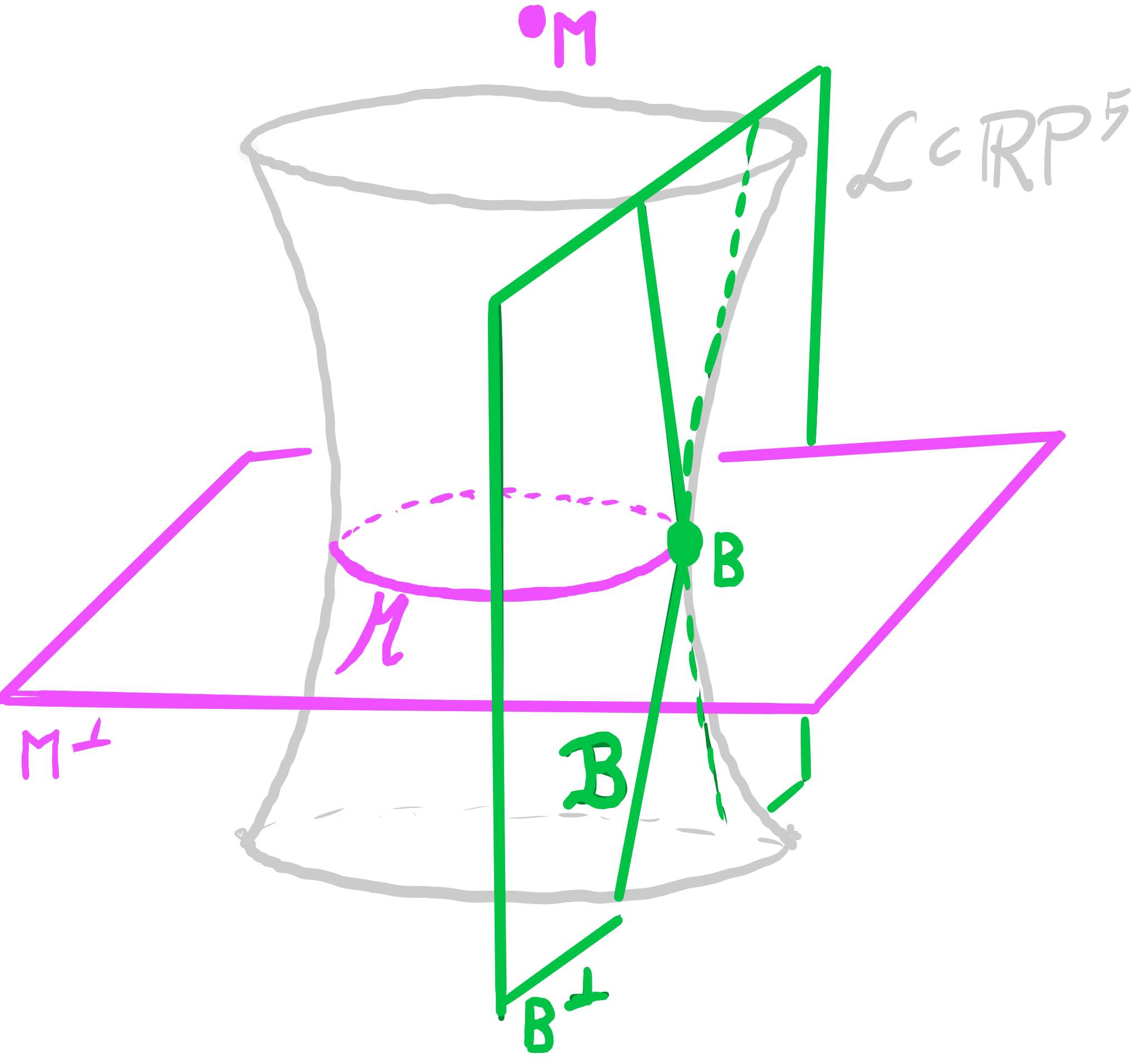
Let $\quad b : D \rightarrow \R^3 \quad$ be a principal binet.
Let $\quad b_{\mathcal{M}} : D \rightarrow \mathbf{M}^\perp \subset \R\mathrm{P}^5 \quad$ be a Möbius lift of $b$,
and $\quad b_{\mathcal{B}} : D \rightarrow \mathbf{B}^\perp \subset \R\mathrm{P}^5 \quad$ be a Laguerre lift of $b$.
Then the map $\quad b_{\mathcal{L}} = b_{\mathcal{M}} \vee b_{\mathcal{B}} : D \rightarrow \mathrm{Lines}(\R\mathrm{P}^5) \quad$ is called a Lie lift of $b$.
Let $\quad b : D \rightarrow \R^3 \quad$ be a principal binet.
Let $\quad b_{\mathcal{M}} : D \rightarrow \mathbf{M}^\perp \subset \R\mathrm{P}^5 \quad$ be a Möbius lift of $b$,
and $\quad b_{\mathcal{B}} : D \rightarrow \mathbf{B}^\perp \subset \R\mathrm{P}^5 \quad$ be a Laguerre lift of $b$.
Then the map $\quad b_{\mathcal{L}} = b_{\mathcal{M}} \vee b_{\mathcal{B}} : D \rightarrow \mathrm{Lines}(\R\mathrm{P}^5) \quad$ is called a Lie lift of $b$.
Theorem:
The Lie lift $~ b_{\mathcal{L}} : D \rightarrow \left\{\text{lines in } \R P^5\right\} ~$ of a principal binet satisfies:
The Lie lift $~ b_{\mathcal{L}} : D \rightarrow \left\{\text{lines in } \R P^5\right\} ~$ of a principal binet satisfies:
- adjacent lines intersect
- $b_{\mathcal{L}}(v) \perp b_{\mathcal{L}}(f) \quad$ for incident $v \in V$ and $f \in F$
Conclusion:
Principal binets in $\R^3$ can be lifted to polar line bicongruences in $\R\mathrm{P}^5$.
Vice versa, polar line bicongruences in $\R\mathrm{P}^5$ project to principal binets in $\R^3$.
Thus, principal binets are Lie invariant.
Principal binets in $\R^3$ can be lifted to polar line bicongruences in $\R\mathrm{P}^5$.
Vice versa, polar line bicongruences in $\R\mathrm{P}^5$ project to principal binets in $\R^3$.
Thus, principal binets are Lie invariant.
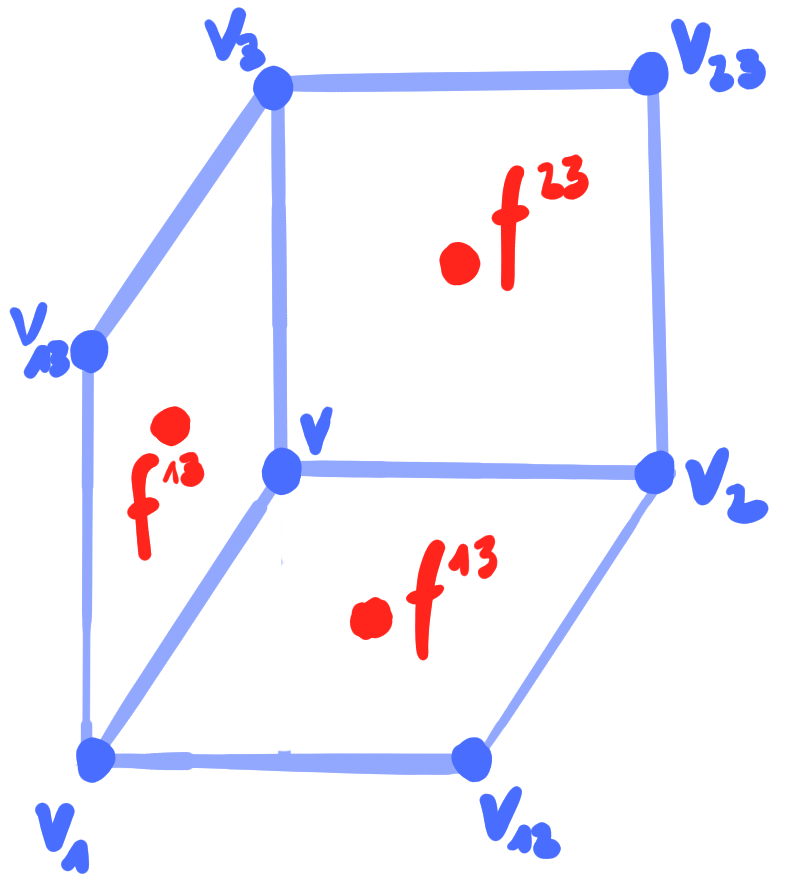
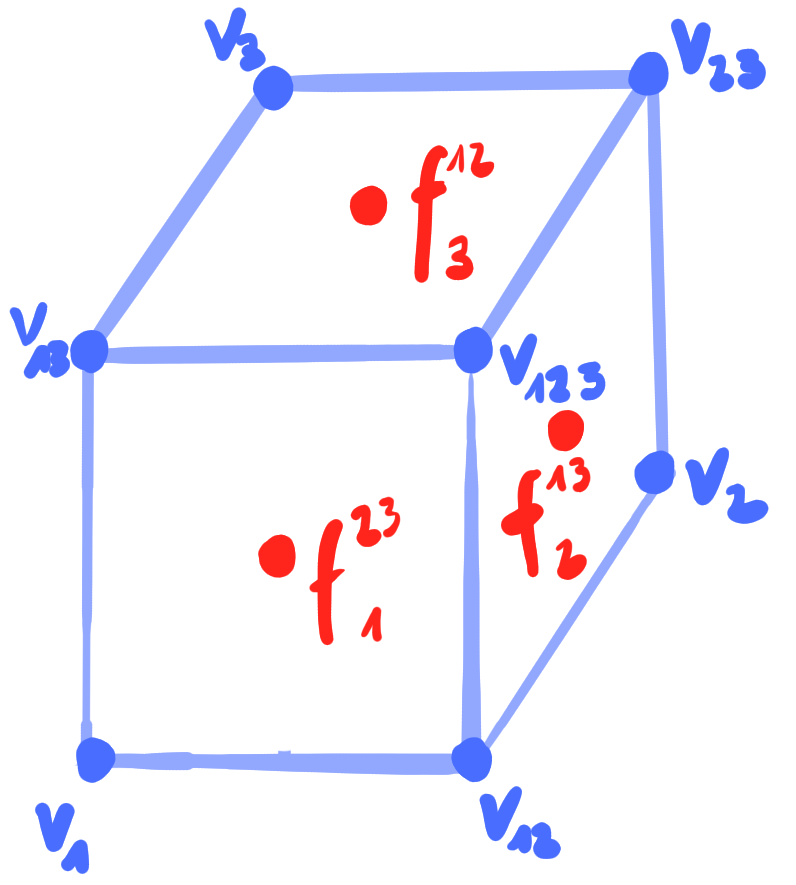
Define
conjugate binets on $\mathbb{Z}^N$ as maps $\mathbb{Z}^N \cup F(\mathbb{Z}^N) \rightarrow \mathbb{R}\mathrm{P}^n$
Theorem:
Conjugate binets are a multi-dimensional consistent 3D-systems.
Theorem:
Polar conjugate binets in $\mathbb{R}\mathrm{P}^4$ are a consistent reduction of conjugate binets in $\mathbb{R}\mathrm{P}^4$.
Corollary:
Principal binets in $\R^3$ are a consistent reduction of conjugate binets in $\R^3$.
|
|
Kœnigs Binets [ADT25+]
Definition:
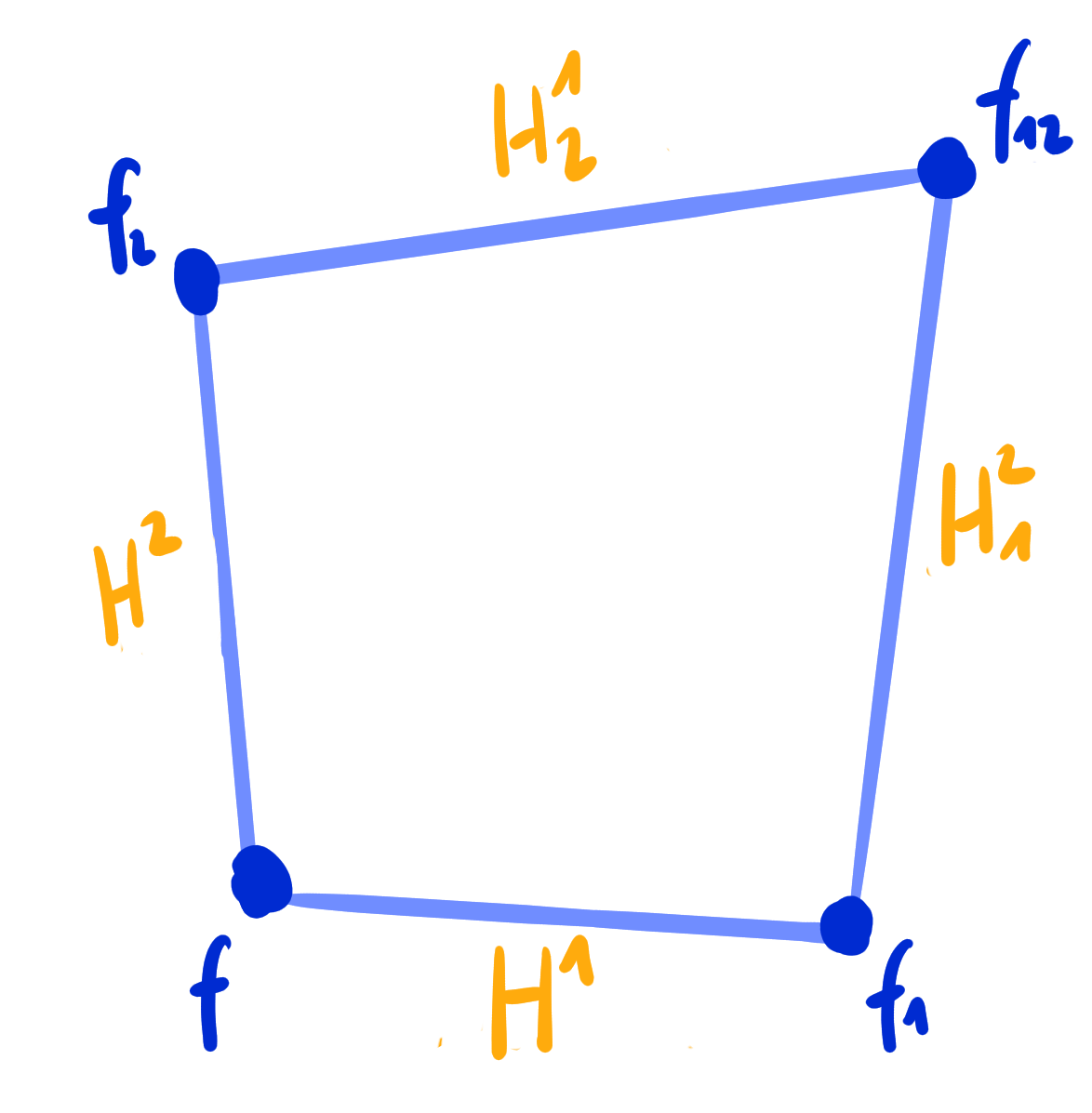
Let $~ f = [\hat f] : \Z^2 \rightarrow \R\mathrm{P}^n~$ be a Q-net with
\[
\small
A\hat f + B\hat f_1 + C\hat f_{12} + D\hat f_2 = 0.
\]
Then
\[
\small
H^1 := \mathrm{cr}(f, F^1, f_1, F^1_{\bar 2}) = \frac{D_{\bar 2}B}{C_{\bar 2}A},
\qquad
H^2 := \mathrm{cr}(f, F^2_{\bar 1}, f_2, F^2) = \frac{AC_{\bar 1}}{DB_{\bar 1}},
\]
are called the discrete Laplace invariants of $[\hat f]$.

Definition:
A BS-Kœnigs net is a Q-net $~f : \Z^2 \rightarrow \R\mathrm{P}^n~$ such that
at every vertex the discrete Laplace invariants satisfy \[ \small H^1 \cdot H^2 \cdot H^1_{\bar 1} \cdot H^2_{\bar 2} = 1. \]
at every vertex the discrete Laplace invariants satisfy \[ \small H^1 \cdot H^2 \cdot H^1_{\bar 1} \cdot H^2_{\bar 2} = 1. \]
- Geometric characterization by coplanar diagonal intersection points.
- Algebraic characterization by homogeneous lift that satisfies a discrete "face based" Moutard equation.
Definition:
Let $f, f^* : \Z^2 \rightarrow \R^n \subset \R\mathrm{P}^n$ be two Q-nets.
Then $f^*$ is a BS-Christoffel dual of $f$ if there exists $\nu : \Z^2 \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_1} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_2} \Delta_2 f \]
Then $f^*$ is a BS-Christoffel dual of $f$ if there exists $\nu : \Z^2 \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_1} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_2} \Delta_2 f \]
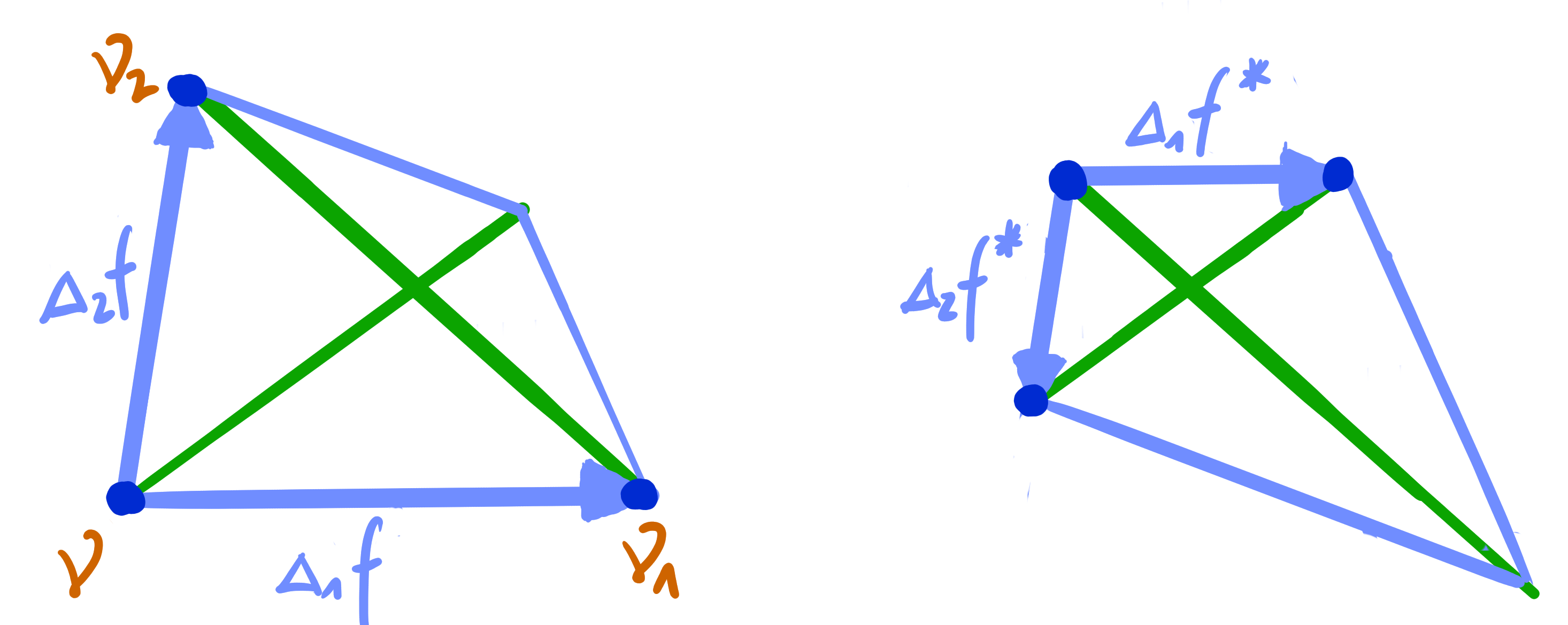
- Equivalently, dual quads have parallel corresponding edges and parallel non-corresponding diagonals.
Theorem:[Bobenko Suris 07]
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a BS-Christoffel dual if and only if $f$ is a BS-Kœnigs net.
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a BS-Christoffel dual if and only if $f$ is a BS-Kœnigs net.
Definition:
A D-Kœnigs net is a Q-net $~f : \Z^2 \rightarrow \R\mathrm{P}^n~$ such that
at every face the discrete Laplace invariants satisfy \[ H^1 \cdot H^2_1 \cdot H^1_2 \cdot H^2 = 1. \]
at every face the discrete Laplace invariants satisfy \[ H^1 \cdot H^2_1 \cdot H^1_2 \cdot H^2 = 1. \]
- Geometric characterization by conic through Laplace points.
- Algebraic characterization by homogeneous lift that satisfies a discrete "vertex based" Moutard equation.
Definition:
Let $f, f^* : \Z^2 \rightarrow \R^n \subset \R\mathrm{P}^n$ be two Q-nets.
Then $f^*$ is a D-Christoffel dual of $f$ if there exists $\nu : F(\Z^2) \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_{\bar 2}} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_{\bar 1}} \Delta_2 f \]
Then $f^*$ is a D-Christoffel dual of $f$ if there exists $\nu : F(\Z^2) \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_{\bar 2}} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_{\bar 1}} \Delta_2 f \]
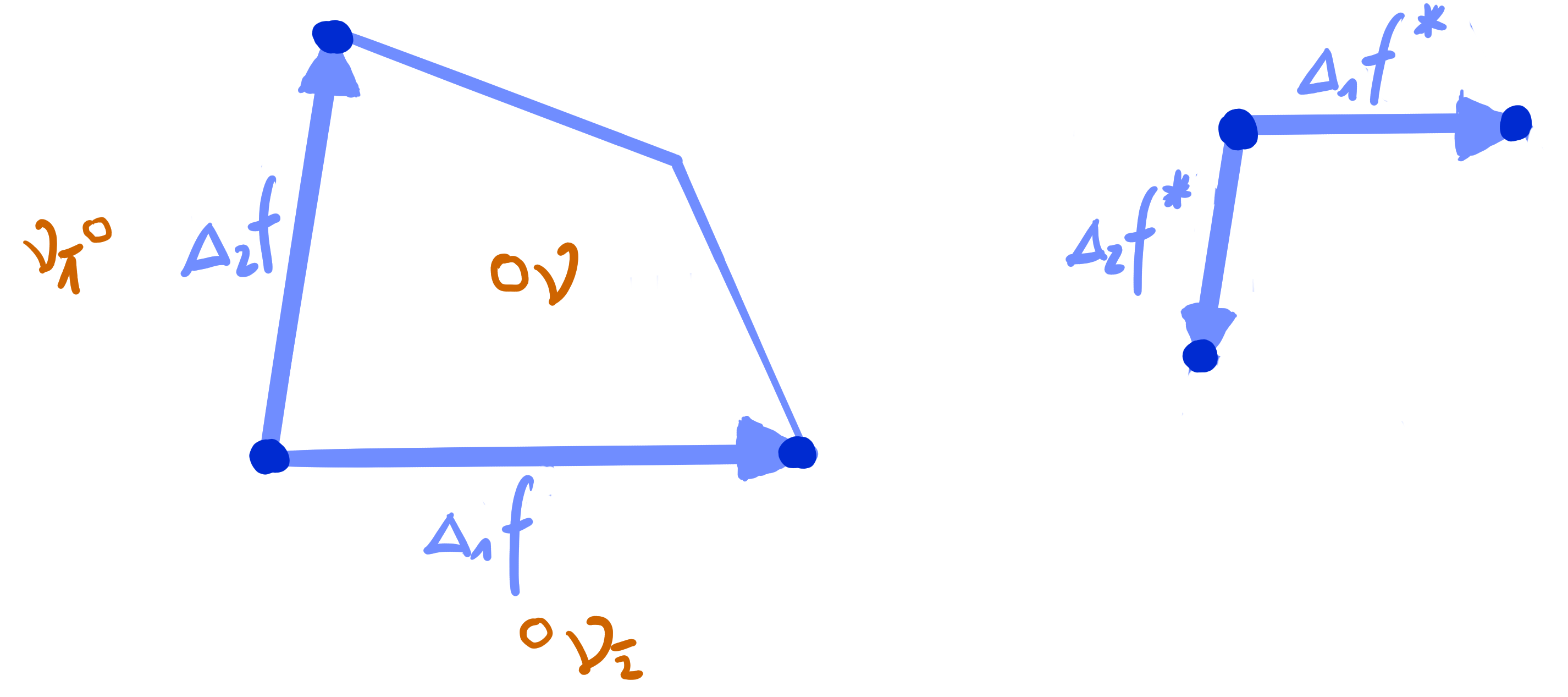
Theorem:[ADT25+]
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a D-Christoffel dual if and only if $f$ is a D-Kœnigs net.
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a D-Christoffel dual if and only if $f$ is a D-Kœnigs net.
Theorem: [Bobenko Suris 07]
Let $~f : \Z^2 \rightarrow \R\mathrm{P}^n~$ be a BS-Kœnigs net.
Let $~g : F(\Z^2) \rightarrow \R\mathrm{P}^n$ be the net of diagonal intersection points of $f$.
Then $g$ is a D-Kœnigs net.
Let $~g : F(\Z^2) \rightarrow \R\mathrm{P}^n$ be the net of diagonal intersection points of $f$.
Then $g$ is a D-Kœnigs net.
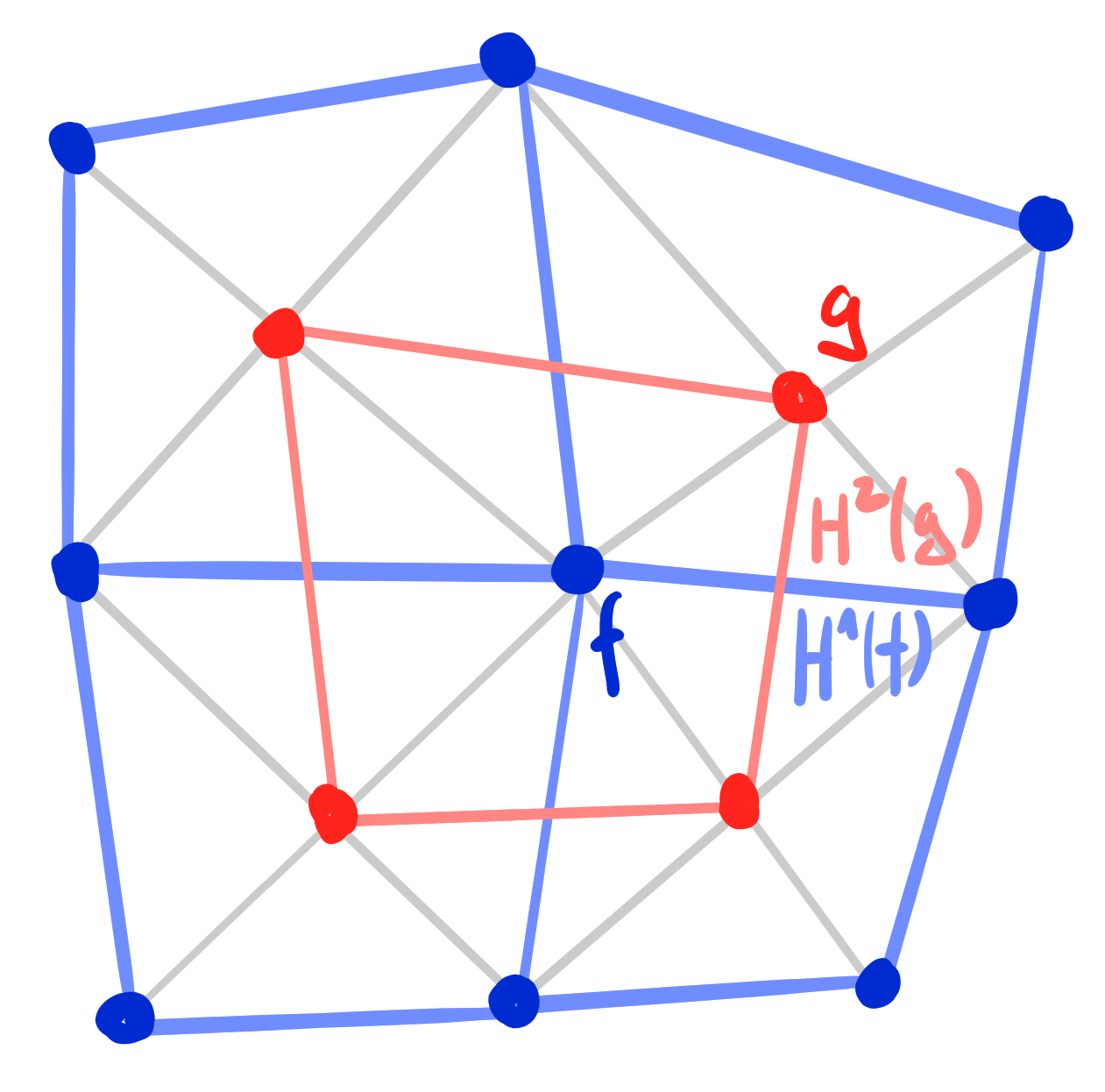
Remark: [Steinmeier 18]
The reverse construction is also possible (D-Kœnigs to BS-Kœnigs).
Theorem: [ADT25+]
The two discrete Laplace invariants on dual edges of $f$ and $g$ satisfy
\[
H^1(f) \cdot H^2(g) = 1, \qquad
H^2(f) \cdot H^1(g) = 1.
\]
Definition:
A Kœnigs binet is a conjugate binet $~b : \Z^2 \cup F(\Z^2) \rightarrow \R\mathrm{P}^n~$such that
at every cross (edge and dual edge) the Laplace invariants satisfy \[ H^1 \cdot H^2 = 1. \]
at every cross (edge and dual edge) the Laplace invariants satisfy \[ H^1 \cdot H^2 = 1. \]
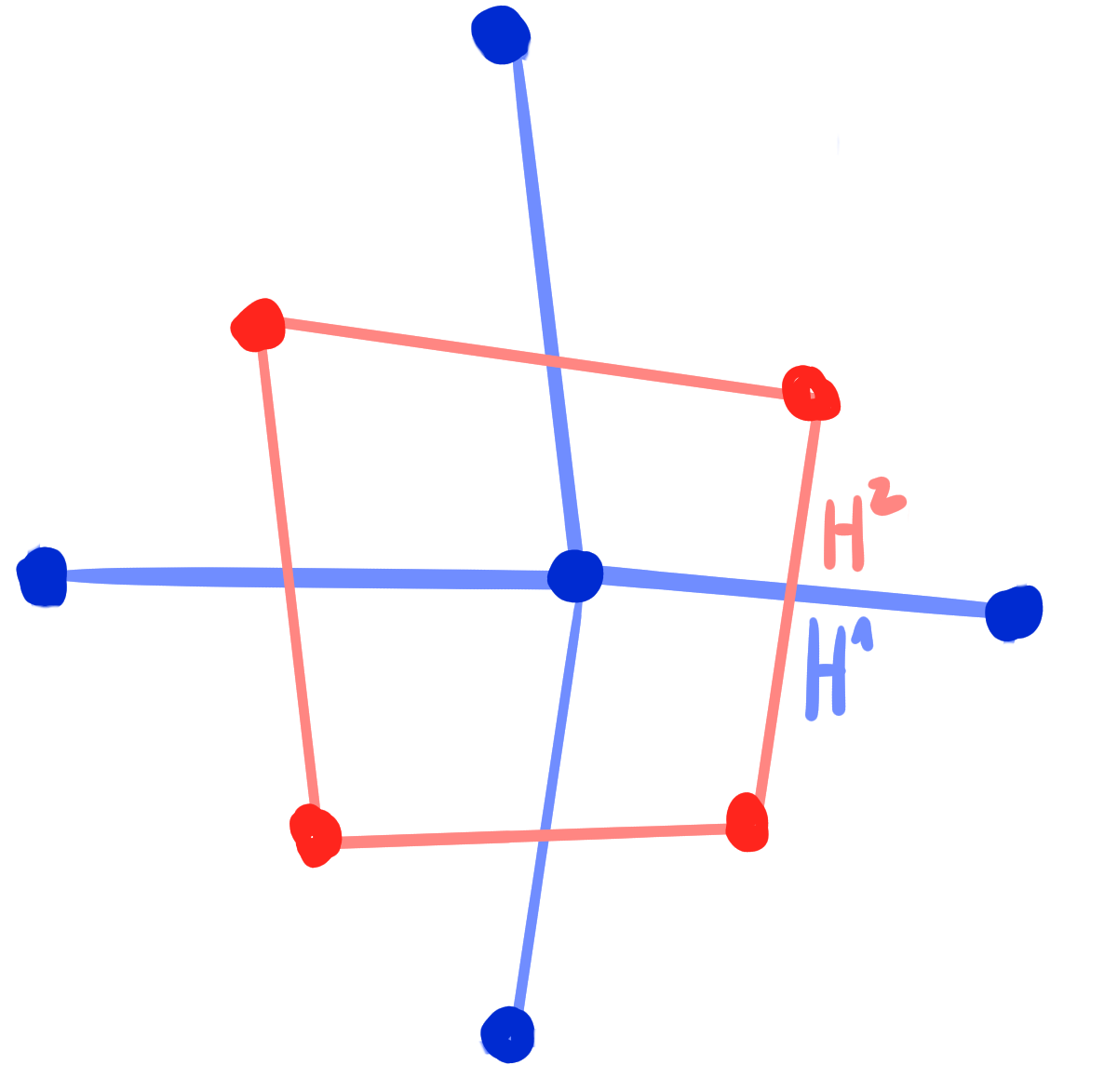
Example:
Pairs of BS-Kœnigs nets and D-Kœnigs nets.
Theorem: [ADT25+]
Let $~ b : \Z^2 \cup F(\Z^2) \rightarrow \R\mathrm{P}^n~$ be a Kœnigs binet.
Then $b|_{\Z^2}$ is a BS-Kœnigs net $~\Leftrightarrow~$ $b|_{F(\Z^2)}$ is a D-Kœnigs net.
Then $b|_{\Z^2}$ is a BS-Kœnigs net $~\Leftrightarrow~$ $b|_{F(\Z^2)}$ is a D-Kœnigs net.
Definition:
Let $~b, b^* : \Z^2 \cup F(\Z^2) \rightarrow \R^n ~$ be two conjugate binets.
Then $b^*$ is called Christoffel dual binet of $b$ if there exists $~\nu : E(\Z^2) \rightarrow \R\setminus \{0\} ~$ such that
\[ \Delta_1 b^* = \frac{1}{\nu^2} \Delta_1 b,\qquad \Delta_2 b^* = -\frac{1}{\nu^2} \Delta_2 b \] at every cross (pair of edge and dual edge).
Then $b^*$ is called Christoffel dual binet of $b$ if there exists $~\nu : E(\Z^2) \rightarrow \R\setminus \{0\} ~$ such that
\[ \Delta_1 b^* = \frac{1}{\nu^2} \Delta_1 b,\qquad \Delta_2 b^* = -\frac{1}{\nu^2} \Delta_2 b \] at every cross (pair of edge and dual edge).
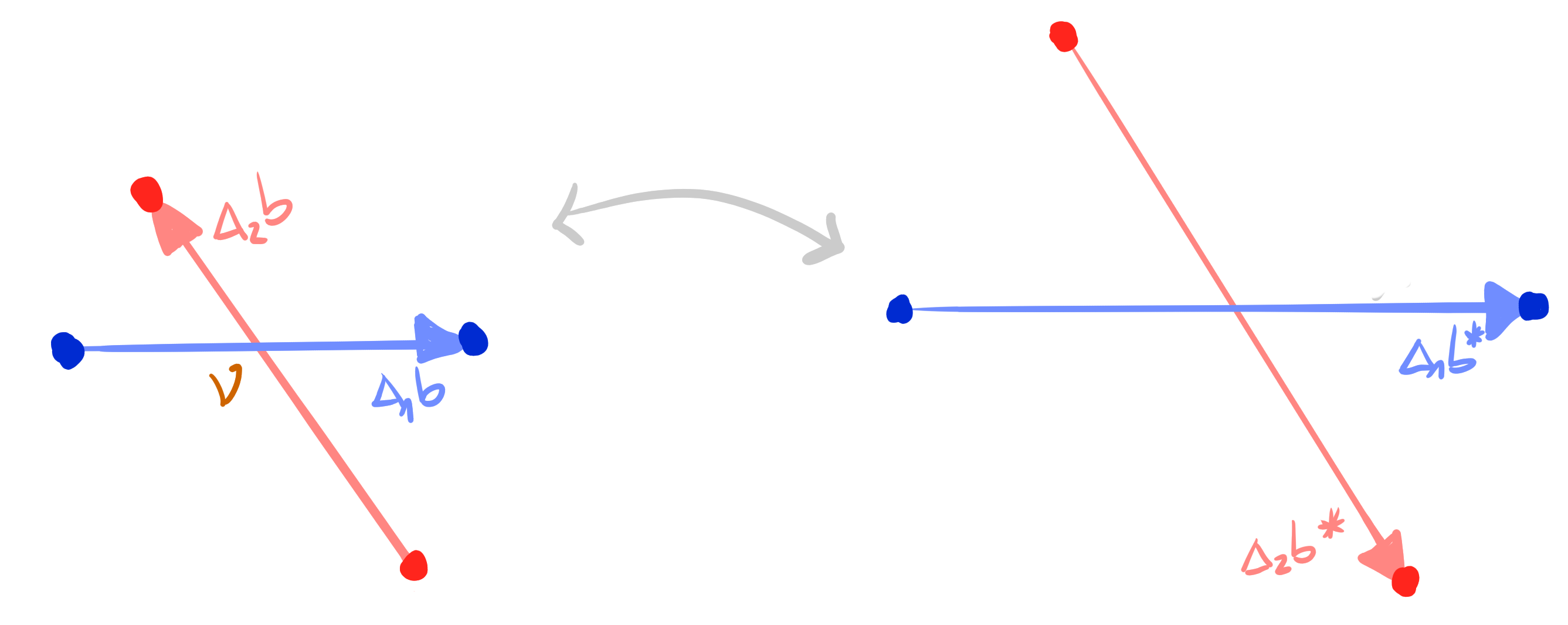
Closing condition for Christoffel dual binet
$
\Leftrightarrow\quad H^1 \cdot H^2 = 1.
$
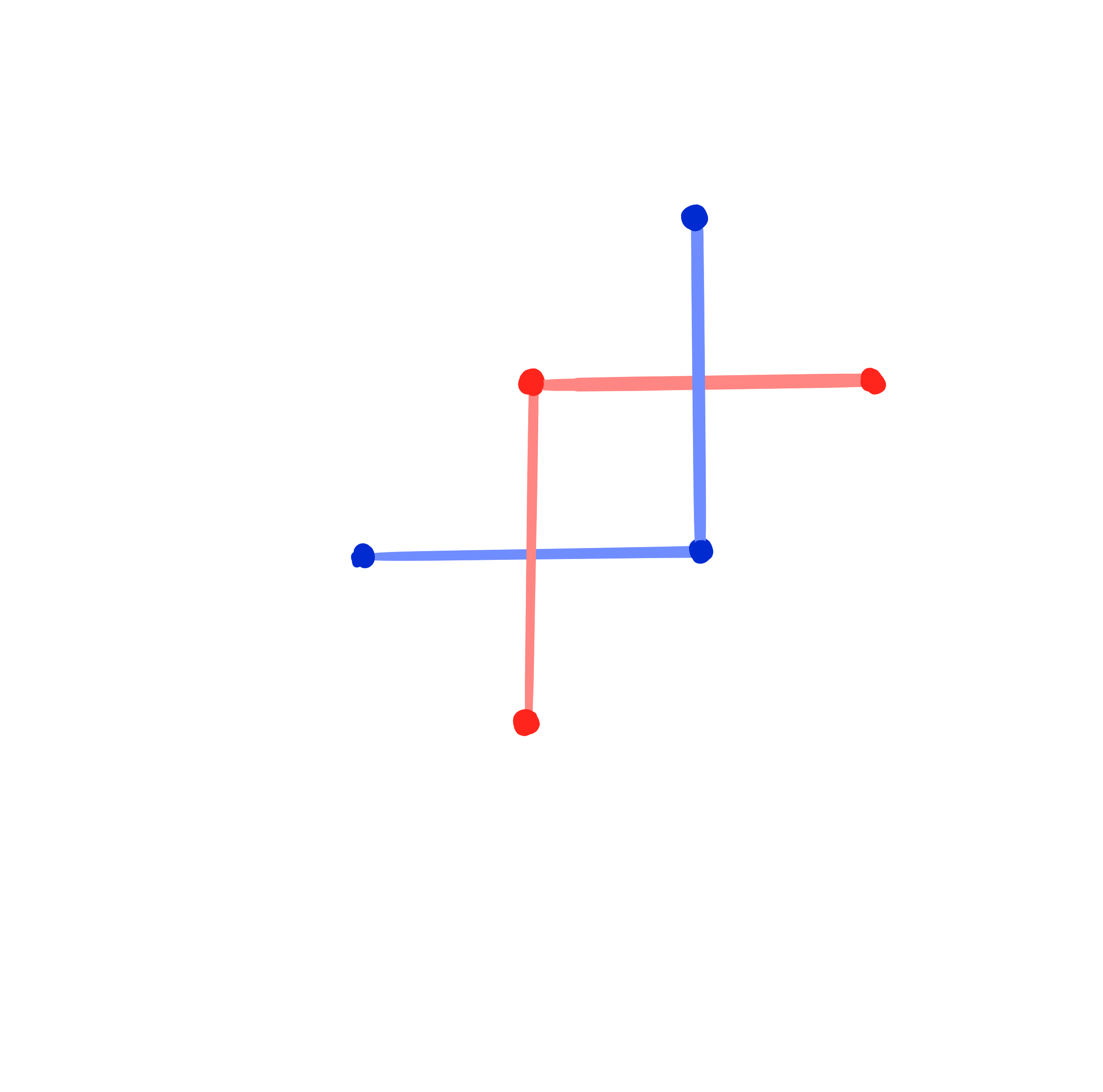
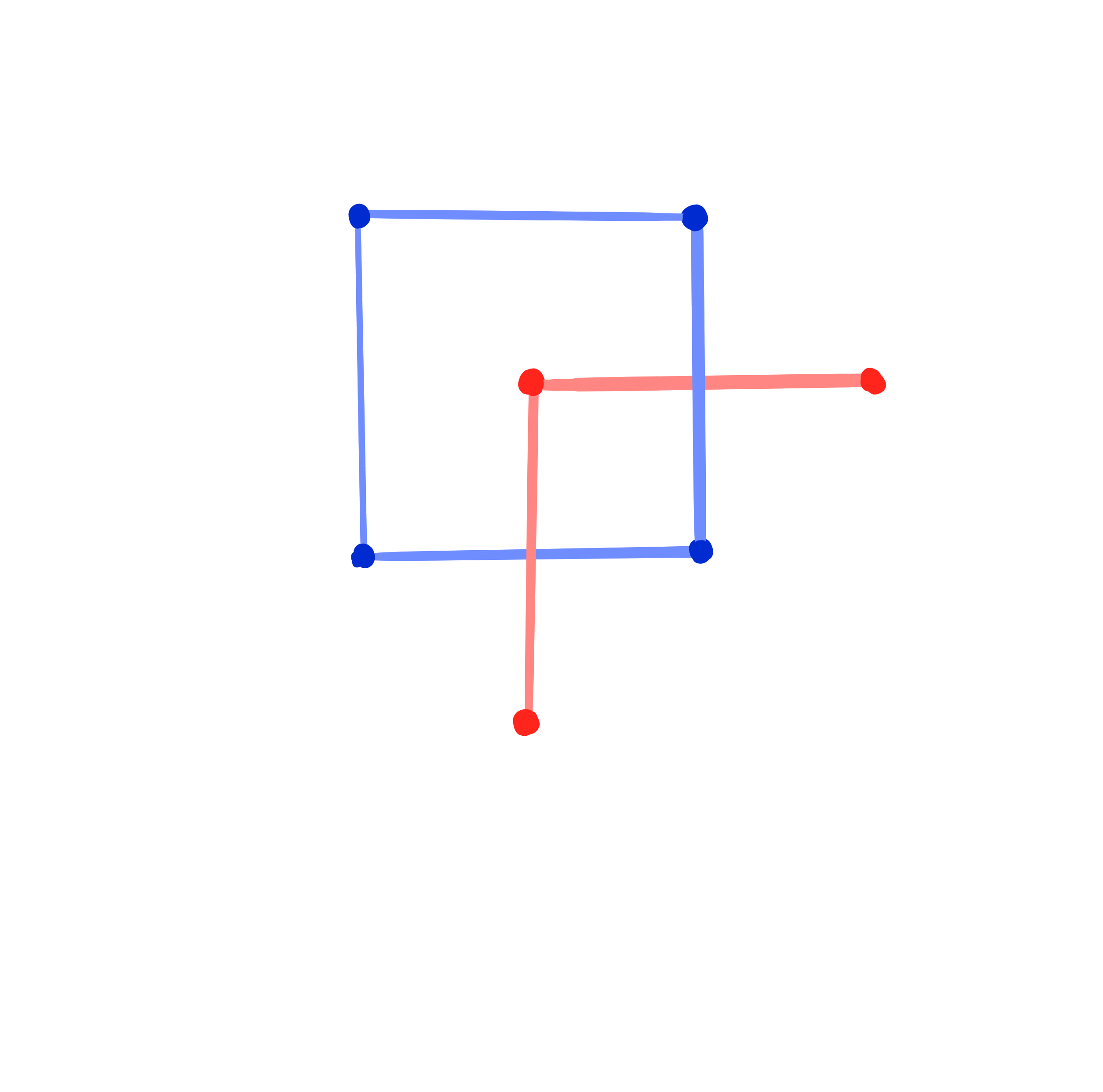
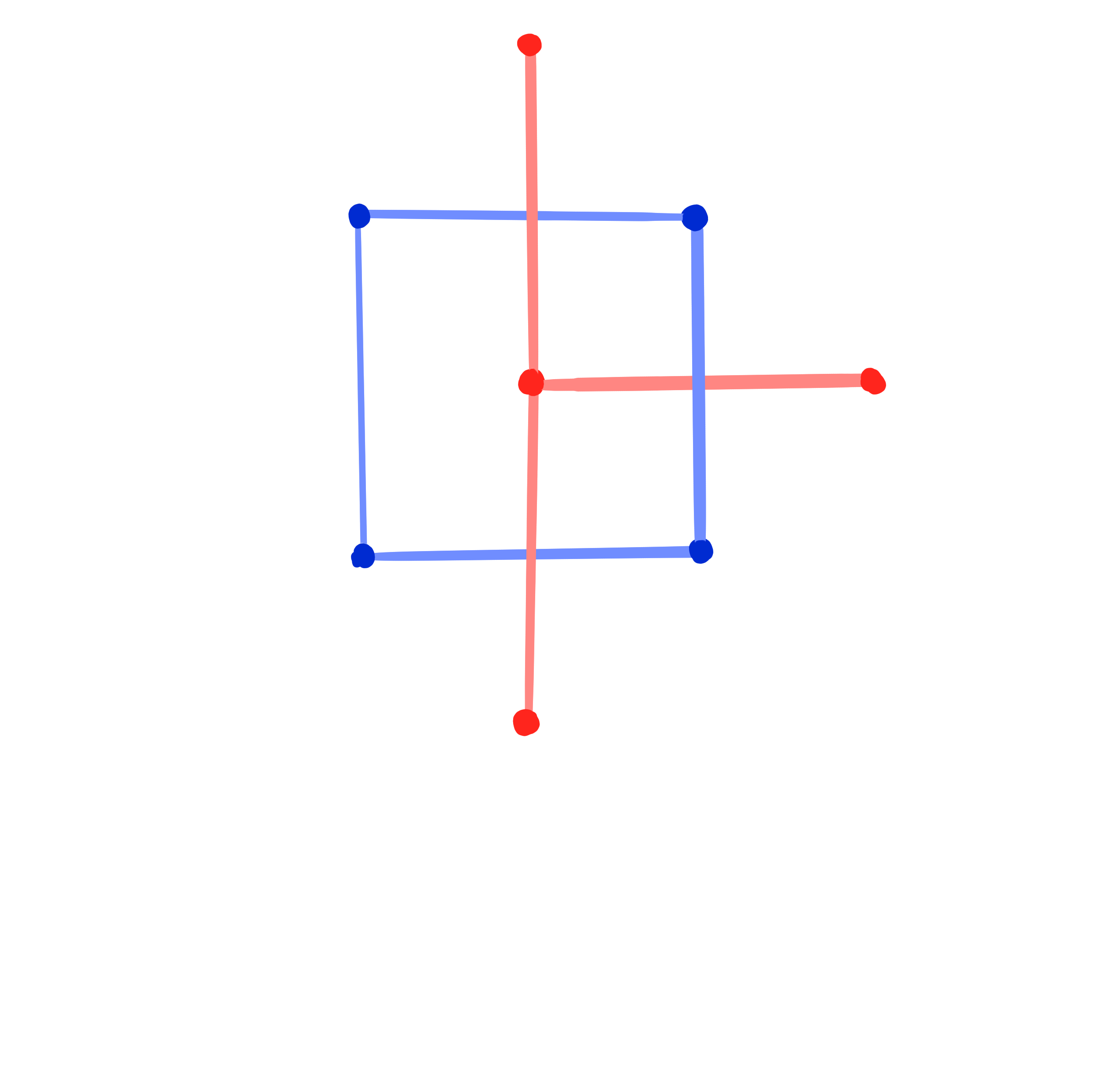
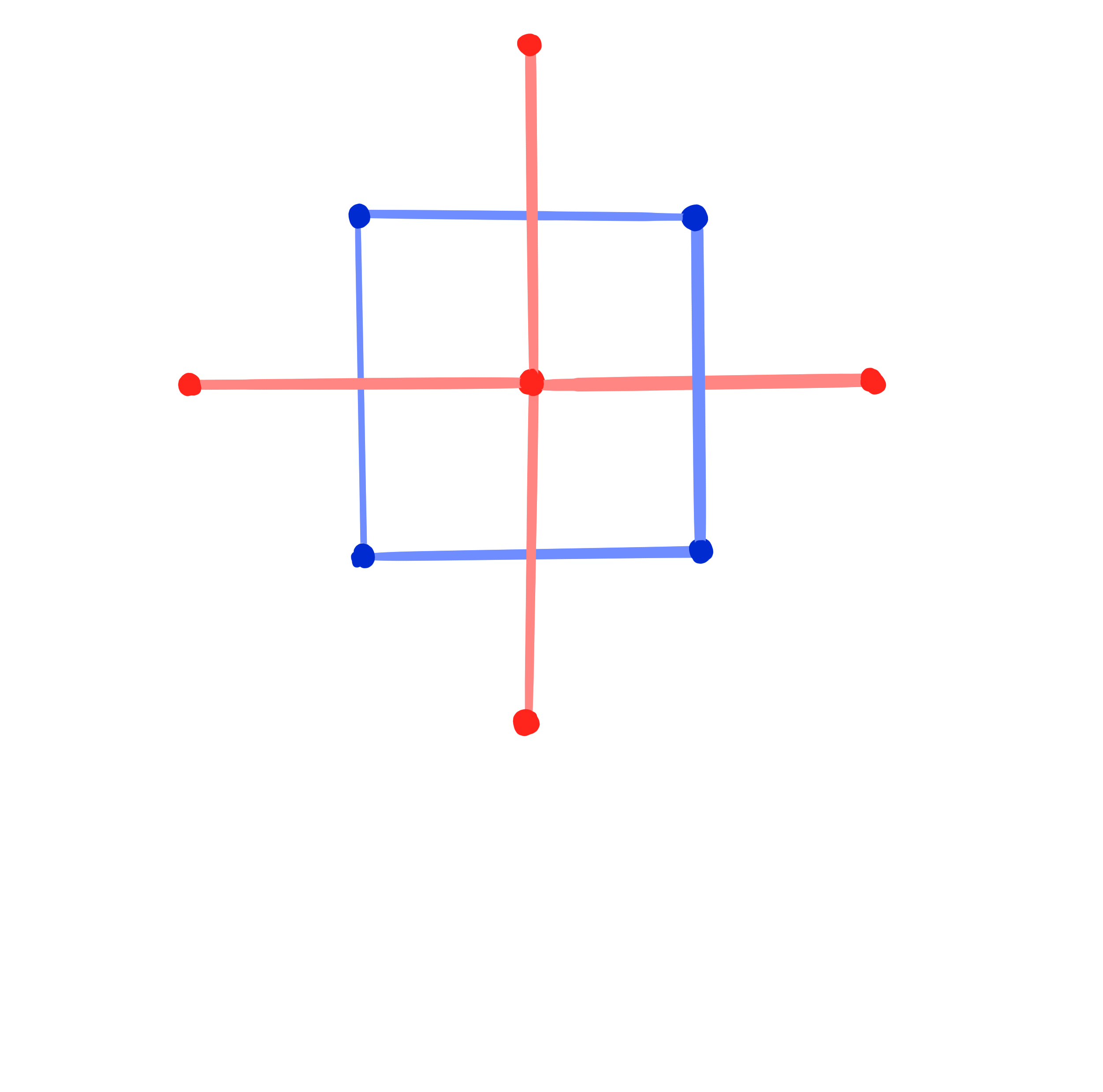
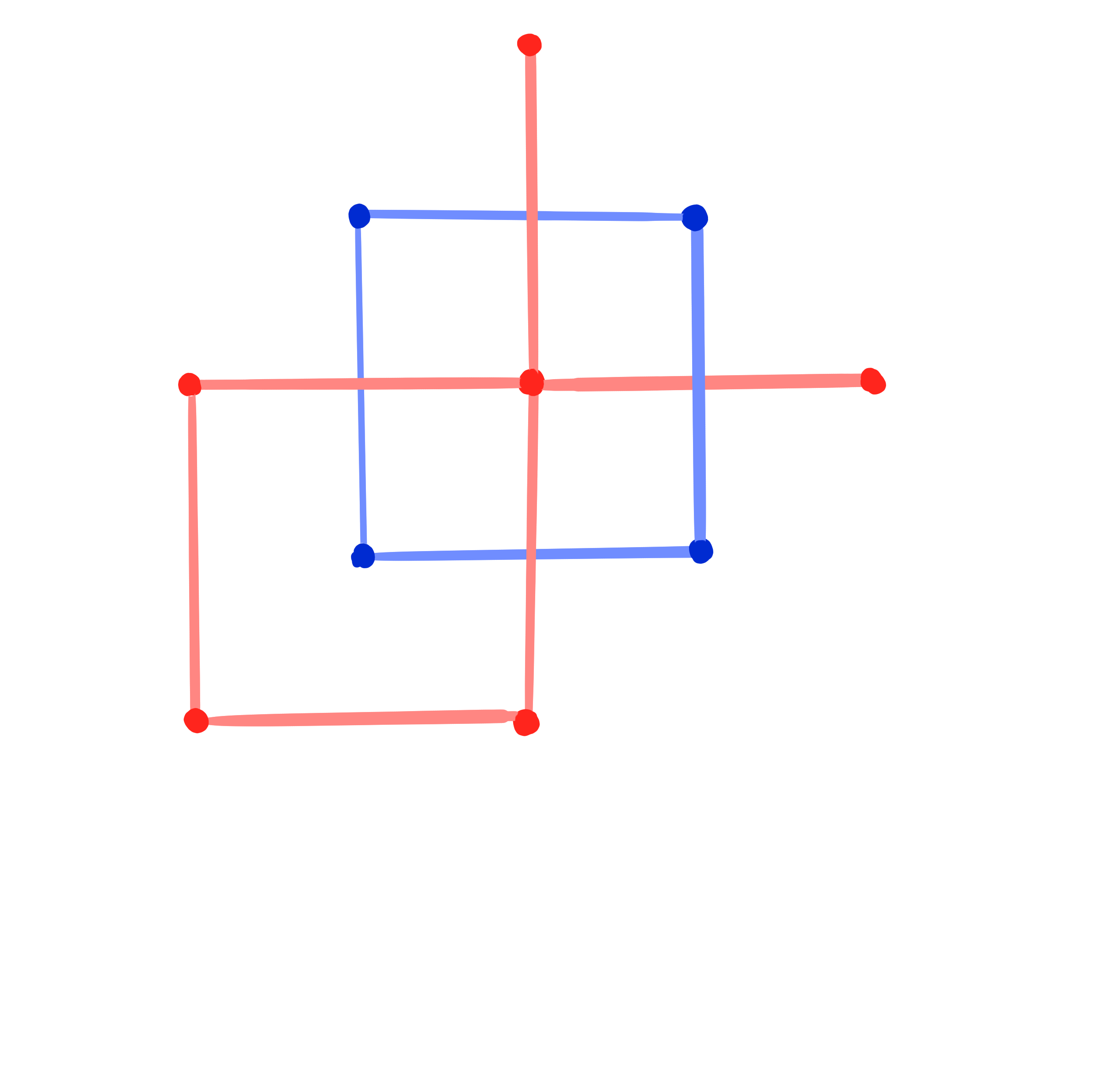
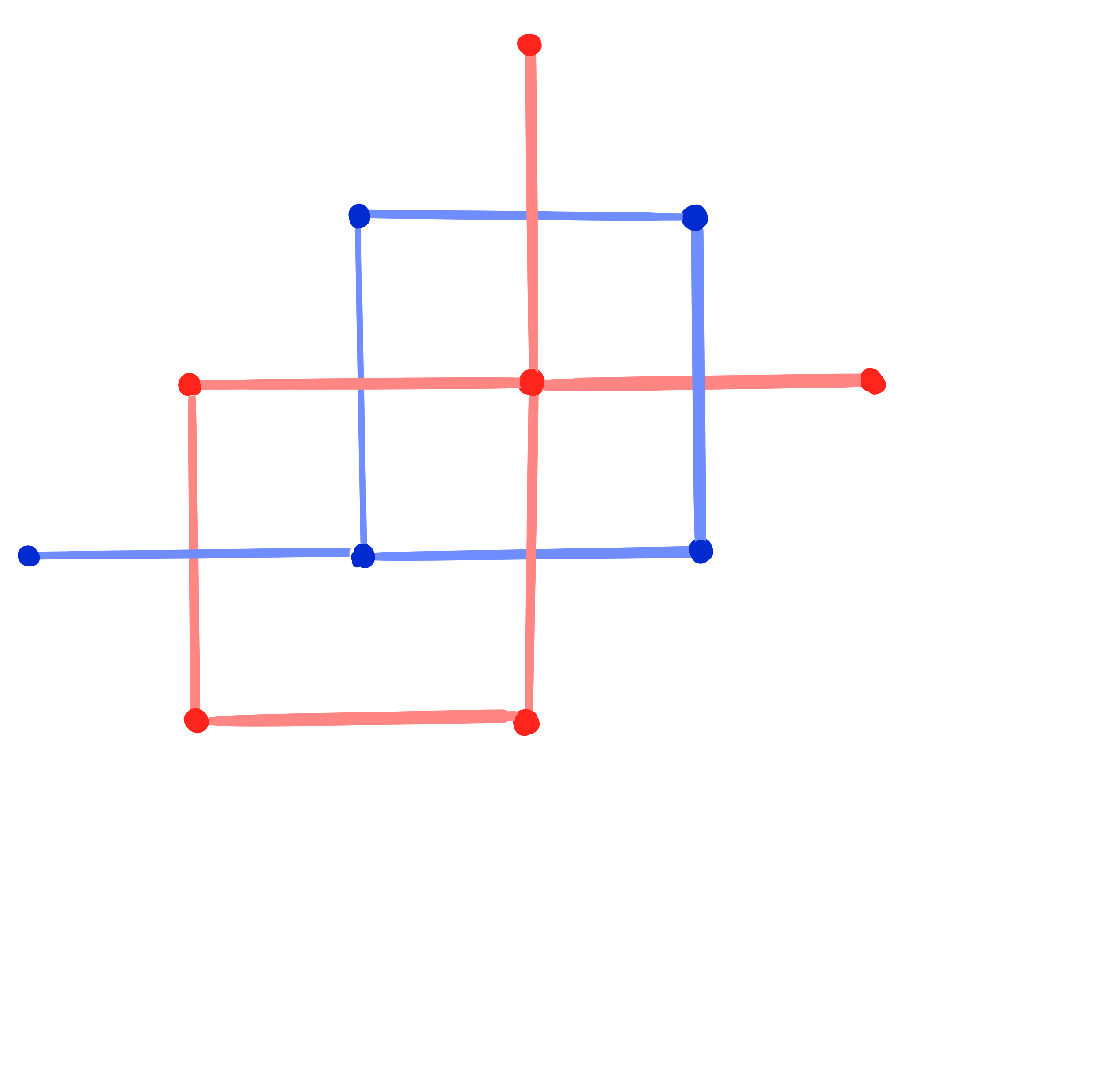
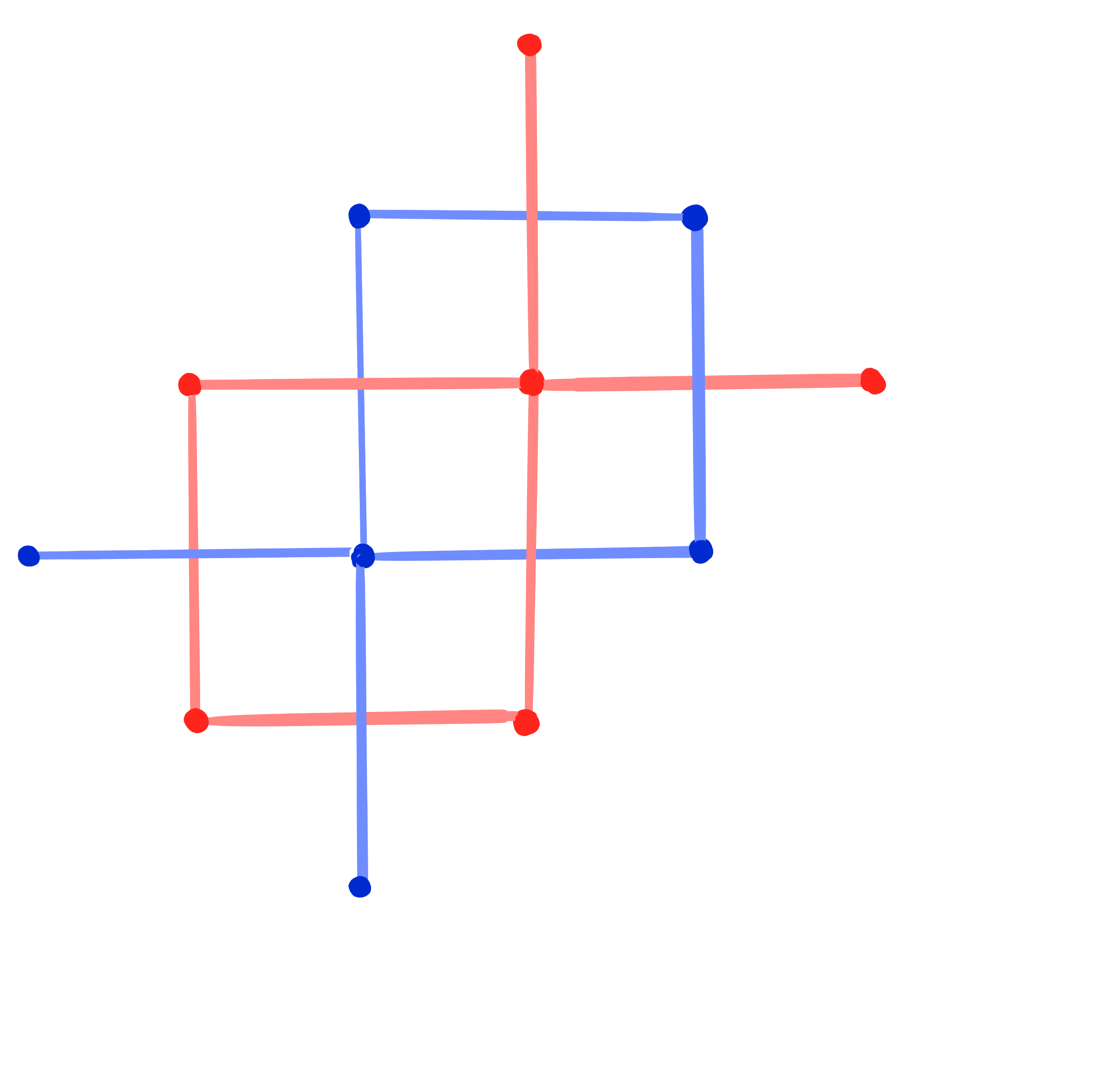
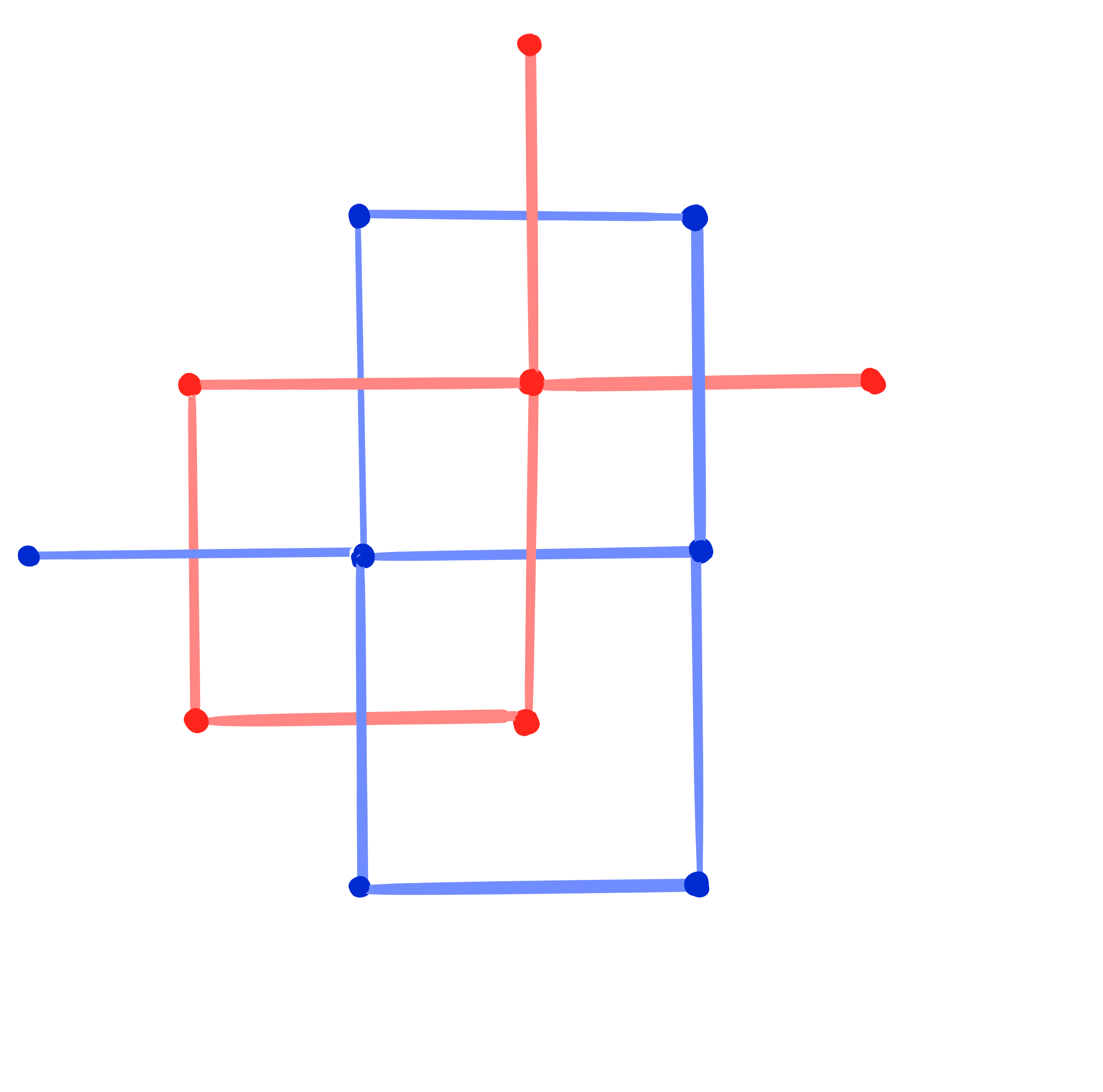
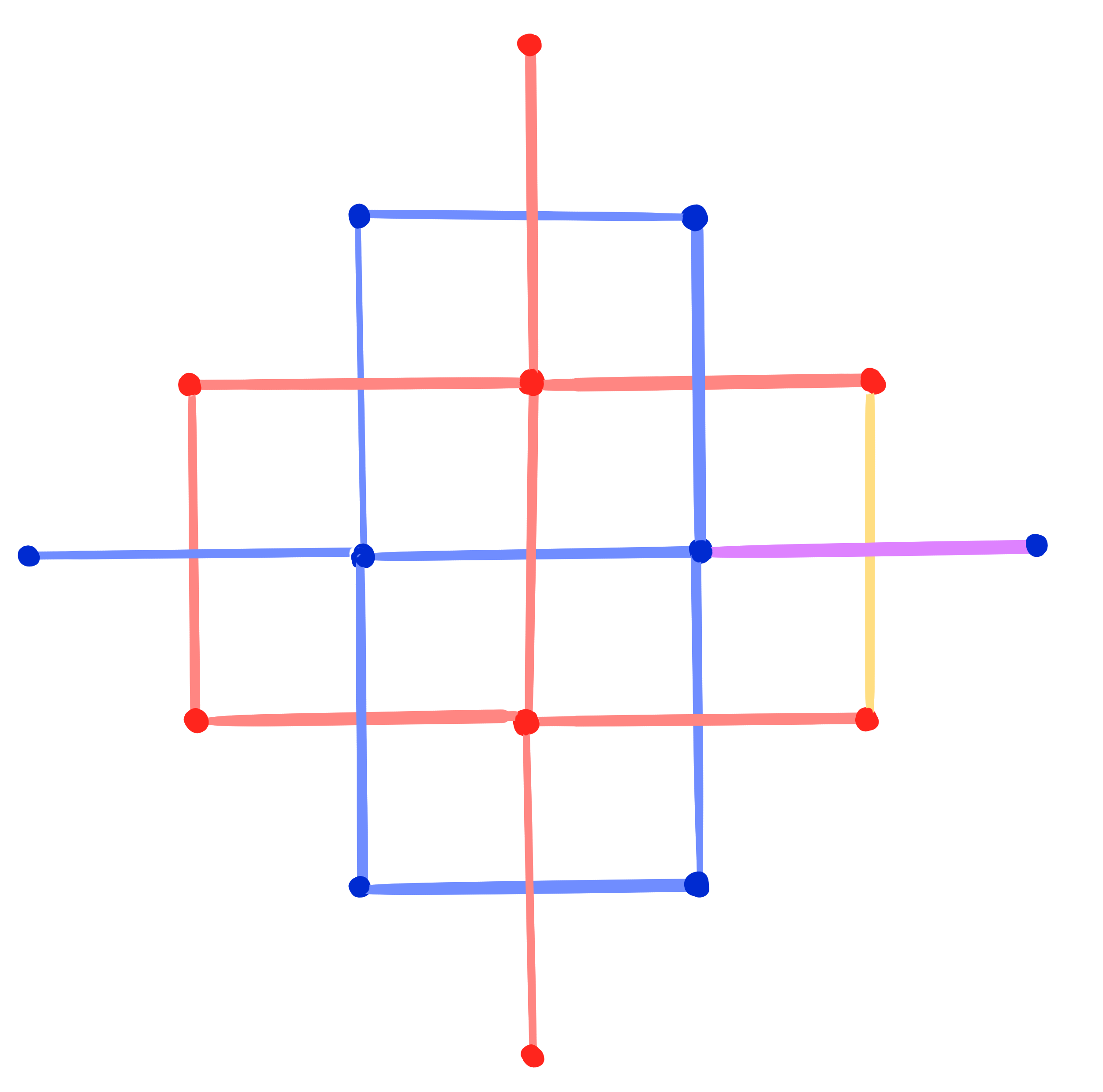
Theorem: [Dellinger 22, ADT25+]
A conjugate binet $b$ has a Christoffel dual binet if and only if $b$ is a Kœnigs binet.
A conjugate binet $b$ has a Christoffel dual binet if and only if $b$ is a Kœnigs binet.
- 2 degrees of freedom (scaling factor at 2 crosses) / 1 degree of freedom up to global scaling
Christoffel dual of a binet comes as a 1-parameter family of binets.
|
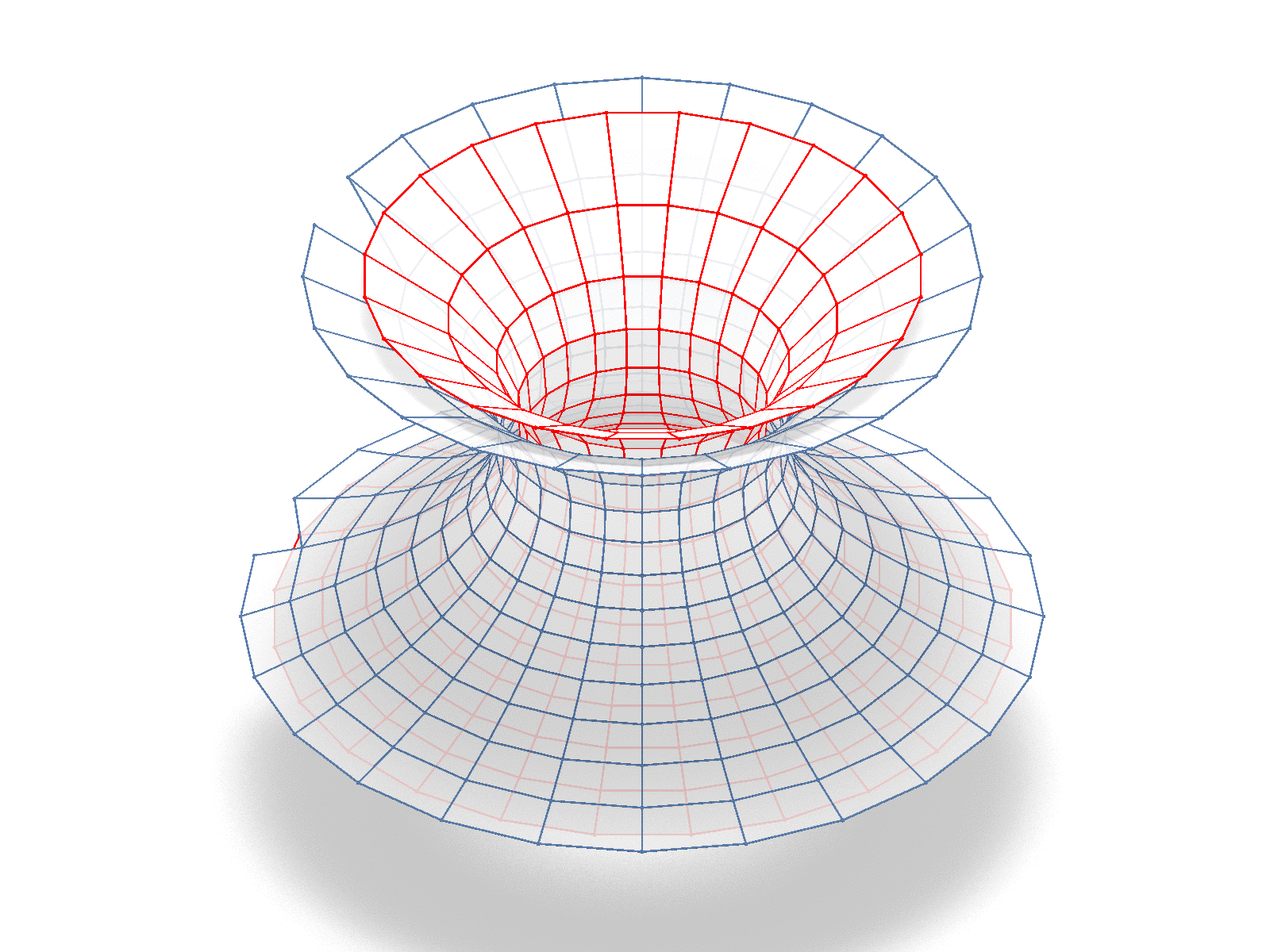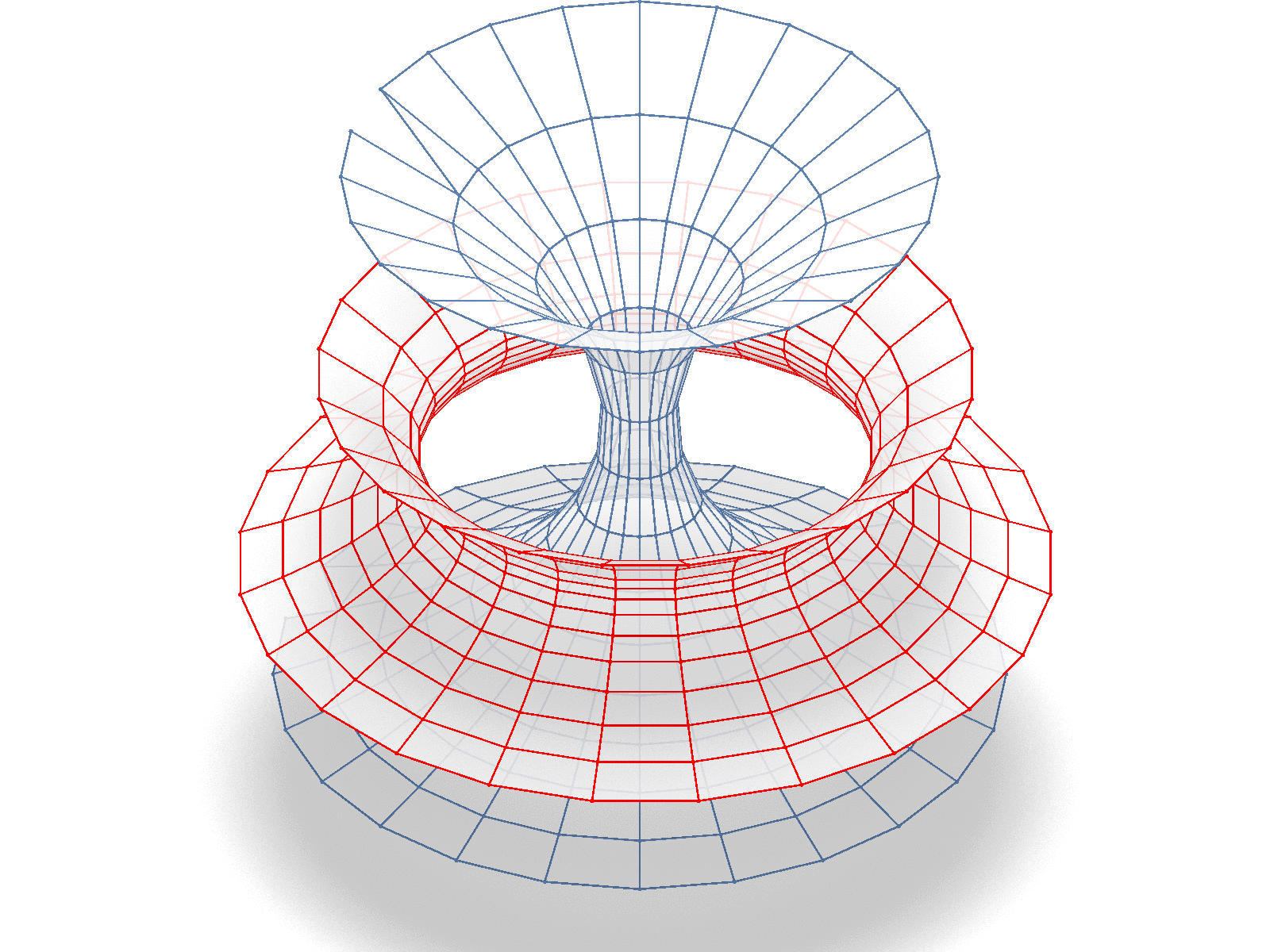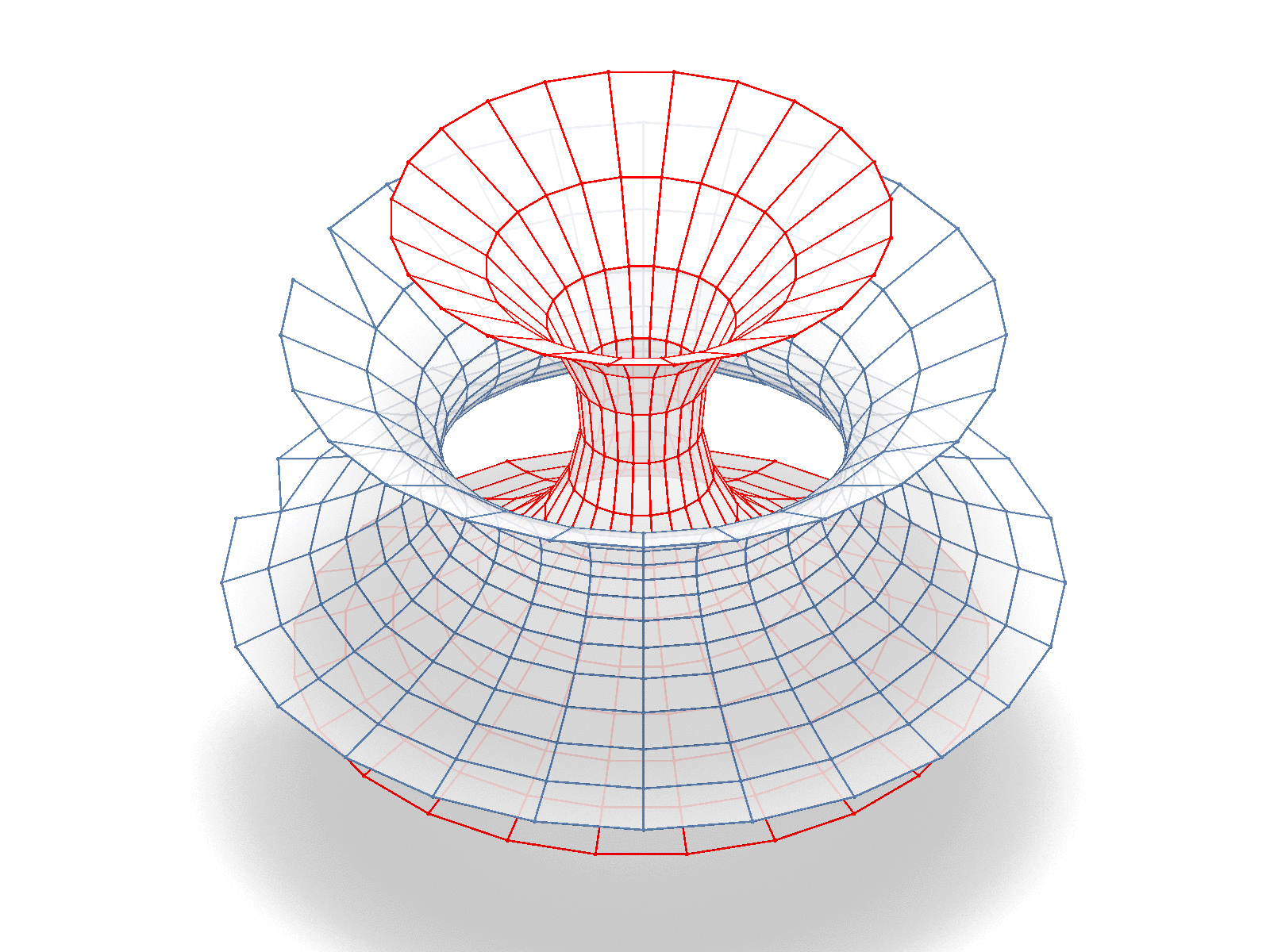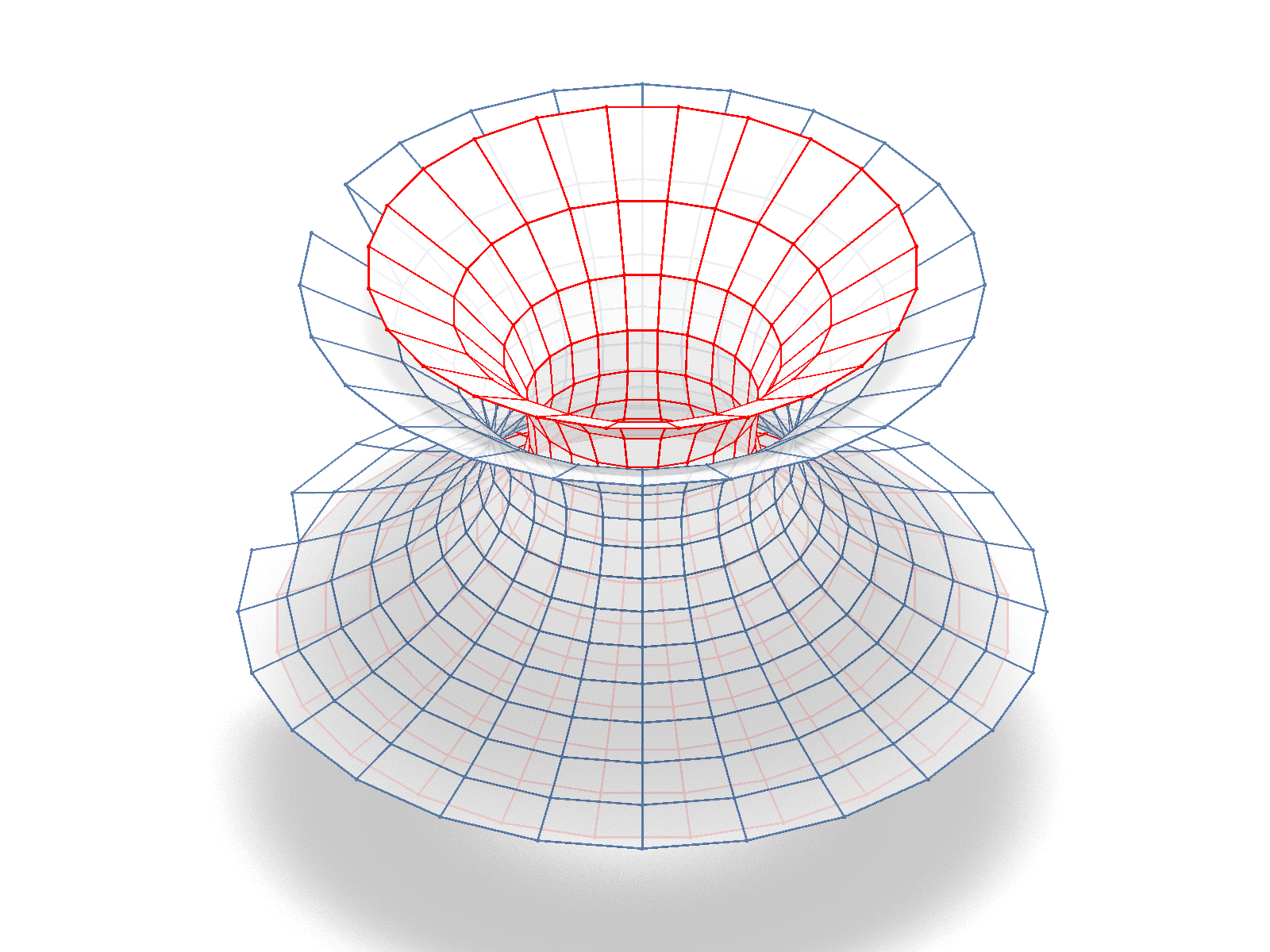
|
- How are binets in the Christoffel dual family related?
Definition:
Let $~b, \hat b : \Z^2 \cup F(\Z^2) \rightarrow \R^n ~$ be two conjugate binets.
Then $b$ and $\hat b$ are called Christoffel equivalent if there exists $~\nu : E(\Z^2) \rightarrow \R\setminus \{0\} ~$ such that
\[ \Delta_1 \hat b = \frac{1}{\nu^2} \Delta_1 b,\qquad \Delta_2 \hat b = \frac{1}{\nu^2} \Delta_2 b \] at every cross (pair of edge and dual edge).
Then $b$ and $\hat b$ are called Christoffel equivalent if there exists $~\nu : E(\Z^2) \rightarrow \R\setminus \{0\} ~$ such that
\[ \Delta_1 \hat b = \frac{1}{\nu^2} \Delta_1 b,\qquad \Delta_2 \hat b = \frac{1}{\nu^2} \Delta_2 b \] at every cross (pair of edge and dual edge).

Theorem:[ADT25+]
Two Christoffel dual binets of a Kœnigs binet are Christoffel equivalent.
Two Christoffel dual binets of a Kœnigs binet are Christoffel equivalent.
Every Christoffel dual of a Kœnigs binet has a 1-parameter family of Christoffel equivalent Christoffel dual binets.

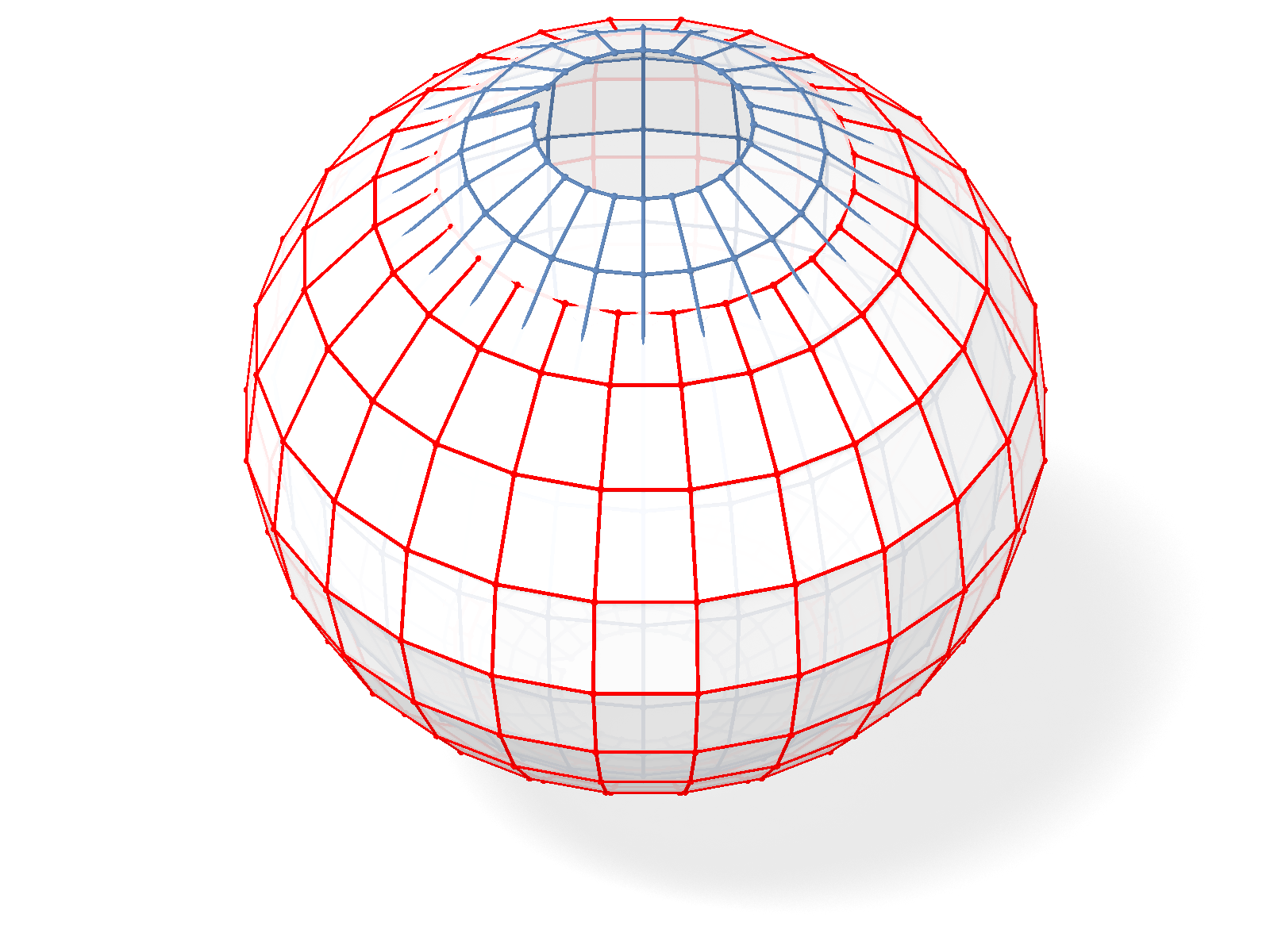
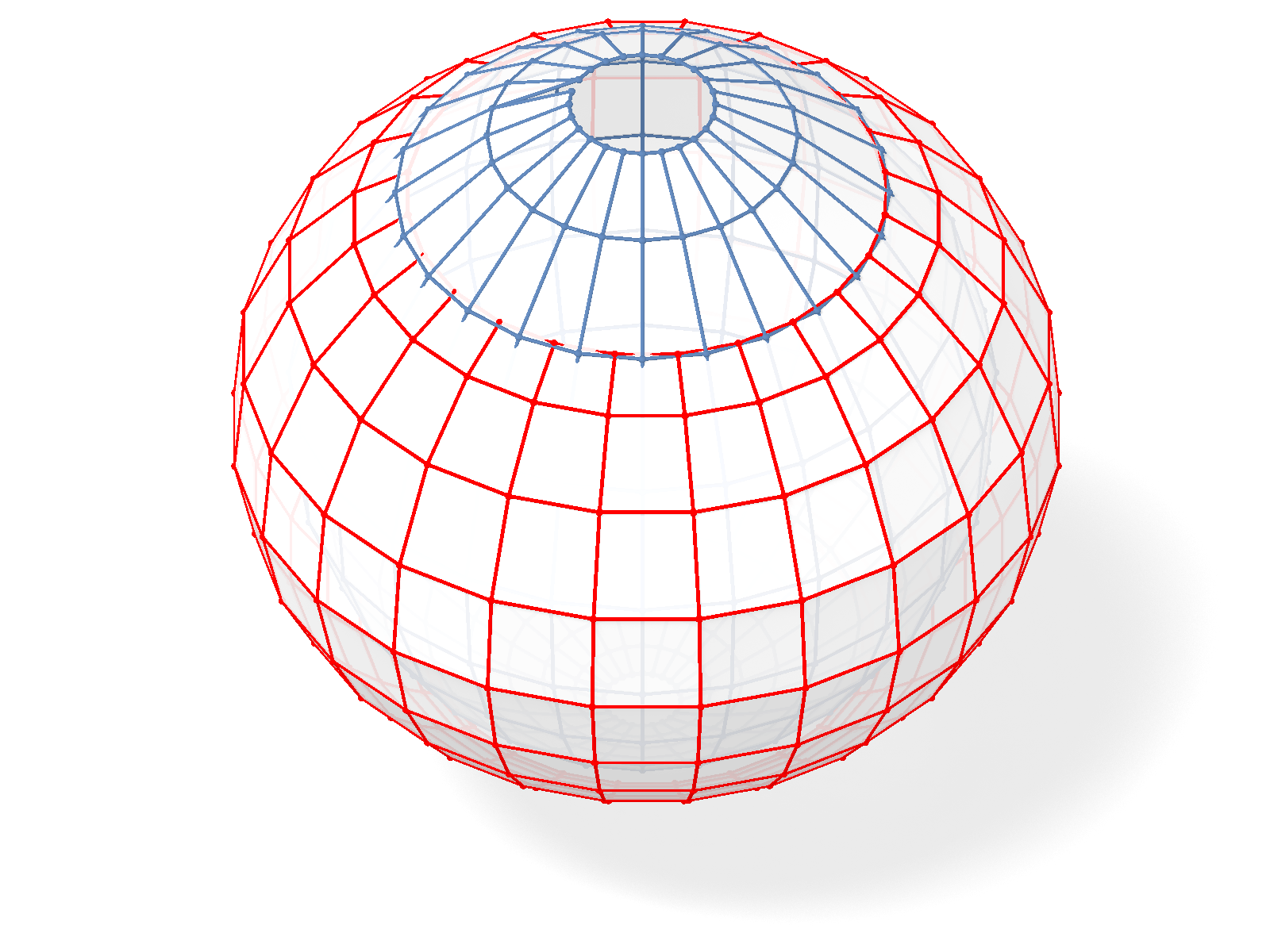
|

|
- Christoffel dual binets come in pairs of 1-parameter families of Christoffel equivalent binets.
Theorem: [ADT25+]
A conjugate binet $b$ has a Christoffel equivalent binet if and only if $b$ is a Kœnigs binet.
A conjugate binet $b$ has a Christoffel equivalent binet if and only if $b$ is a Kœnigs binet.

-
Conjugate binets which are Christoffel equivalent are conformal Combescure transforms.
Such transformations do not exist in the smooth case.
Theorem:[ADT25+]
Kœnigs binets on $\Z^N$ are a consistent reduction of "conjugate binets" on $\Z^N$ (different definition).
Kœnigs binets on $\Z^N$ are a consistent reduction of "conjugate binets" on $\Z^N$ (different definition).

|

|
Isothermic Binets
Definition:
A binet $D \rightarrow \R^3$ is called isothermic binet if it is a principal binet and a Kœnigs binet.
A binet $D \rightarrow \R^3$ is called isothermic binet if it is a principal binet and a Kœnigs binet.

|

|

|
Example:
S-conical nets (conical and BS-Kœnigs) are isothermic binets.
S-conical nets (conical and BS-Kœnigs) are isothermic binets.
Question:
How to incorporate other classical discretizations of isothermic surfaces?
E.g. circular isothermic nets (circular and BS-Kœnigs).
How to incorporate other classical discretizations of isothermic surfaces?
E.g. circular isothermic nets (circular and BS-Kœnigs).

Thank you!
-
[AT24] Principal binets
Affolter, T. -
[ADT25+] Kœnigs binets
Affolter, Dellinger, T.