Kœnigs binets
Jan Techter
joint work with N. Affolter and F. Dellinger
Discrete Kœnigs nets on $\Z^2$
Discrete Kœnigs nets on $\Z^m$
-
BS-Kœnigs nets
- BS-Christoffel dual
-
D-Kœnigs nets
- D-Christoffel dual
-
Kœnigs binets
- Christoffel dual binets
Discrete Kœnigs nets on $\Z^m$
-
BS-Kœnigs nets
- multi-dimensional consistency
-
D-Kœnigs nets
- multi-dimensional consistency
-
Kœnigs binets
- multi-dimensional consistency
Definition:
A ($2$-dimensional) discrete net is a map $~f = [\hat f] : \Z^2 \rightarrow \R\mathrm{P}^n$.
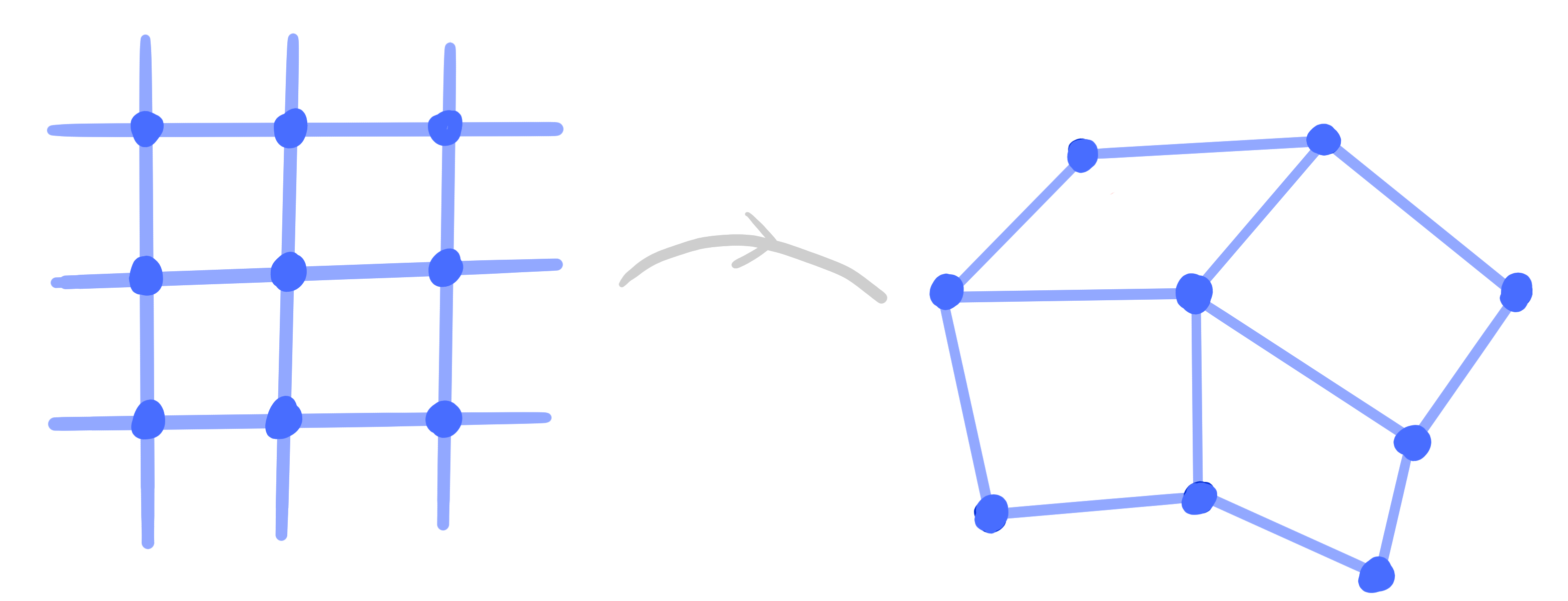
Definition:
A discrete net $~f = [\hat f] : \Z^2 \rightarrow \R\mathrm{P}^n~$ is a discrete conjugate net (Q-net)
\[
\begin{aligned}
:\Leftrightarrow \quad &f, f_1, f_{12}, f_2 ~~\text{lie in a plane}\\
\Leftrightarrow \quad & A \hat f + B\hat f_1 + C\hat f_{12} + D\hat f_2 = 0 ~~\text{with some}~~
A, B, C, D : F(\Z^2) \rightarrow \R\\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad
\text{(discrete Laplace equation)}
\end{aligned}
\]
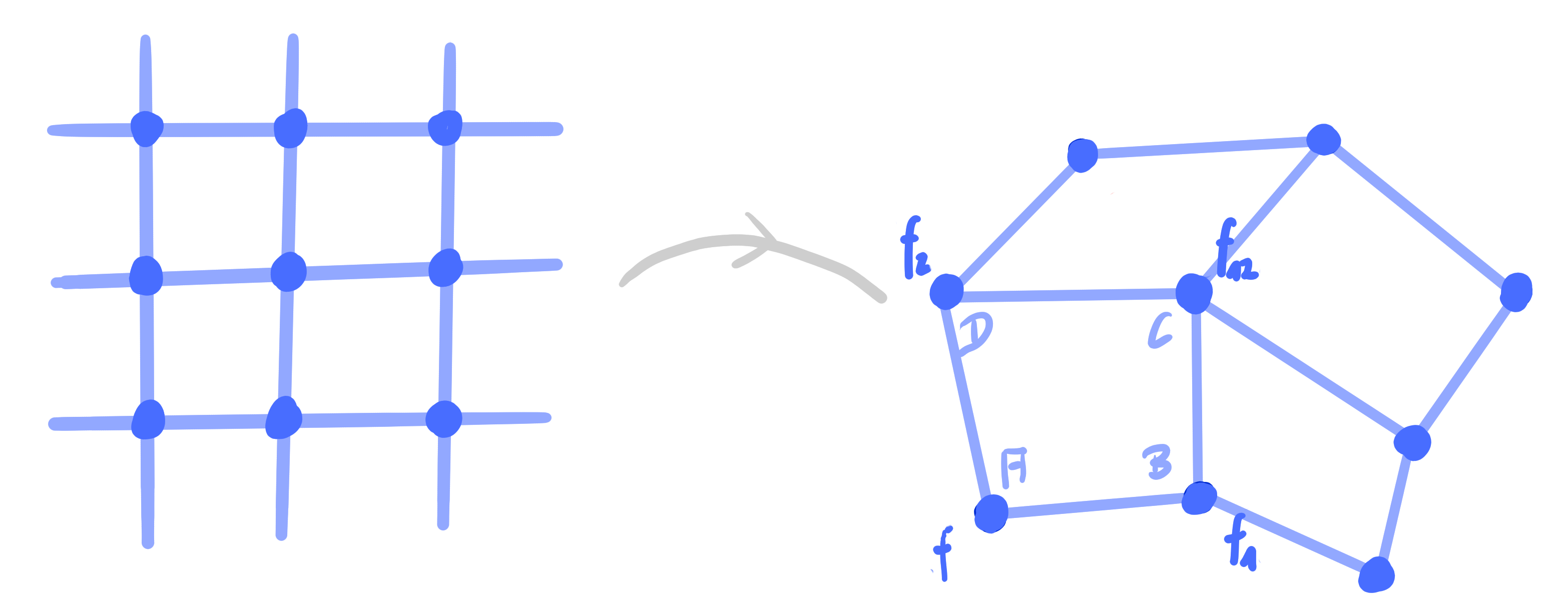
Definition:
Let $~ f = [\hat f] : \Z^2 \rightarrow \R\mathrm{P}^n~$ be a Q-net with
\[
\small
A\hat f + B\hat f_1 + C\hat f_{12} + D\hat f_2 = 0.
\]
Then
\[
\small
H^1 := \mathrm{cr}(f, F^1, f_1, F^1_{\bar 2}) = \frac{D_{\bar 2}B}{C_{\bar 2}A},
\qquad
H^2 := \mathrm{cr}(f, F^2_{\bar 1}, f_2, F^2) = \frac{AC_{\bar 1}}{DB_{\bar 1}},
\]
are called the discrete Laplace invariants of $[\hat f]$.
Definition:
A BS-Kœnigs net is a Q-net $~f : \Z^2 \rightarrow \R\mathrm{P}^n~$ such that
at every vertex the discrete Laplace invariants satisfy \[ \small H^1 \cdot H^2 \cdot H^1_{\bar 1} \cdot H^2_{\bar 2} = 1. \]
at every vertex the discrete Laplace invariants satisfy \[ \small H^1 \cdot H^2 \cdot H^1_{\bar 1} \cdot H^2_{\bar 2} = 1. \]
- Geometric characterization by coplanar diagonal intersection points.
- Algebraic characterization by homogeneous lift that satisfies a discrete "face based" Moutard equation.
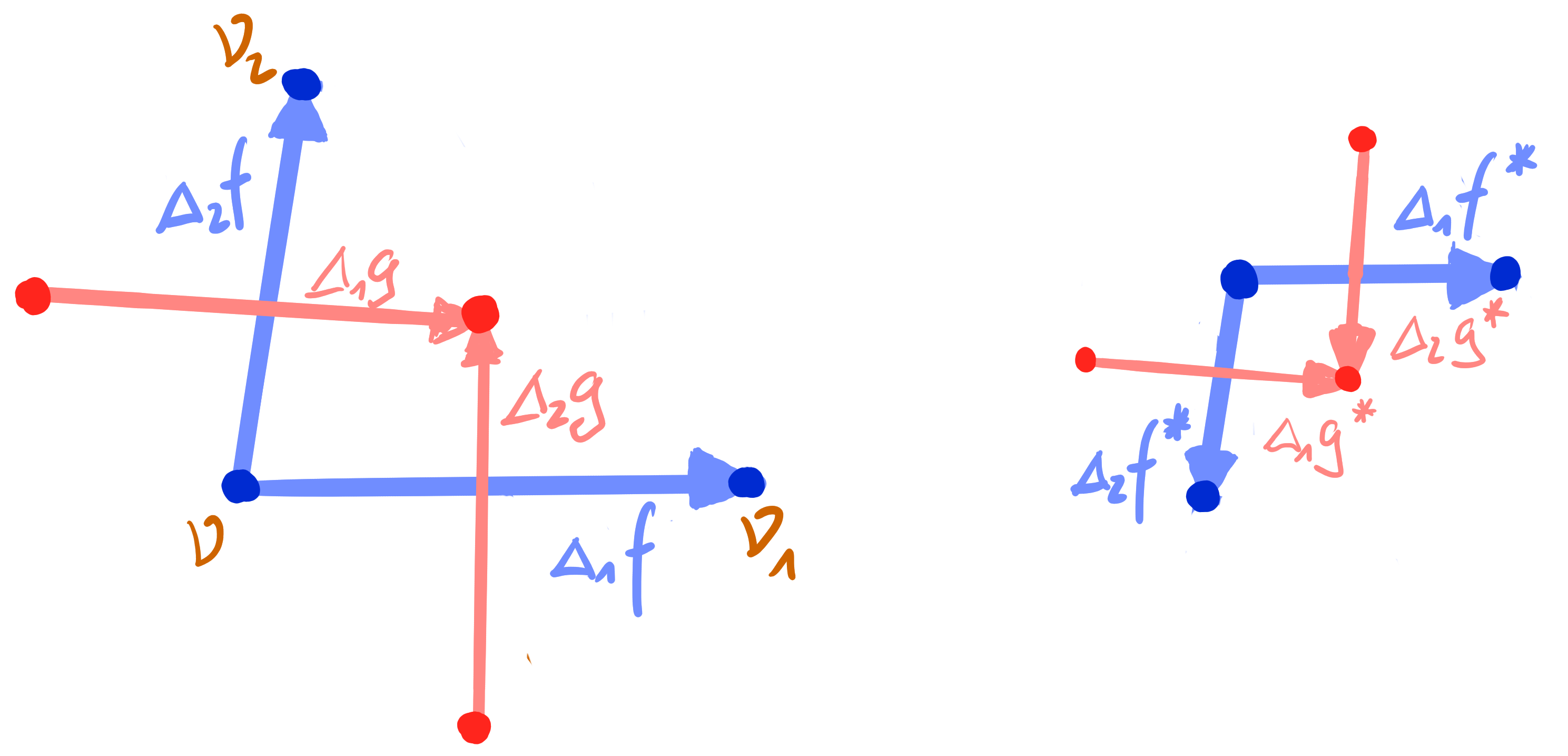
Definition:
Let $f, f^* : \Z^2 \rightarrow \R^n \subset \R\mathrm{P}^n$ be two Q-nets.
Then $f^*$ is a BS-Christoffel dual of $f$ if there exists $\nu : \Z^2 \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_1} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_2} \Delta_2 f \]
Then $f^*$ is a BS-Christoffel dual of $f$ if there exists $\nu : \Z^2 \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_1} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_2} \Delta_2 f \]
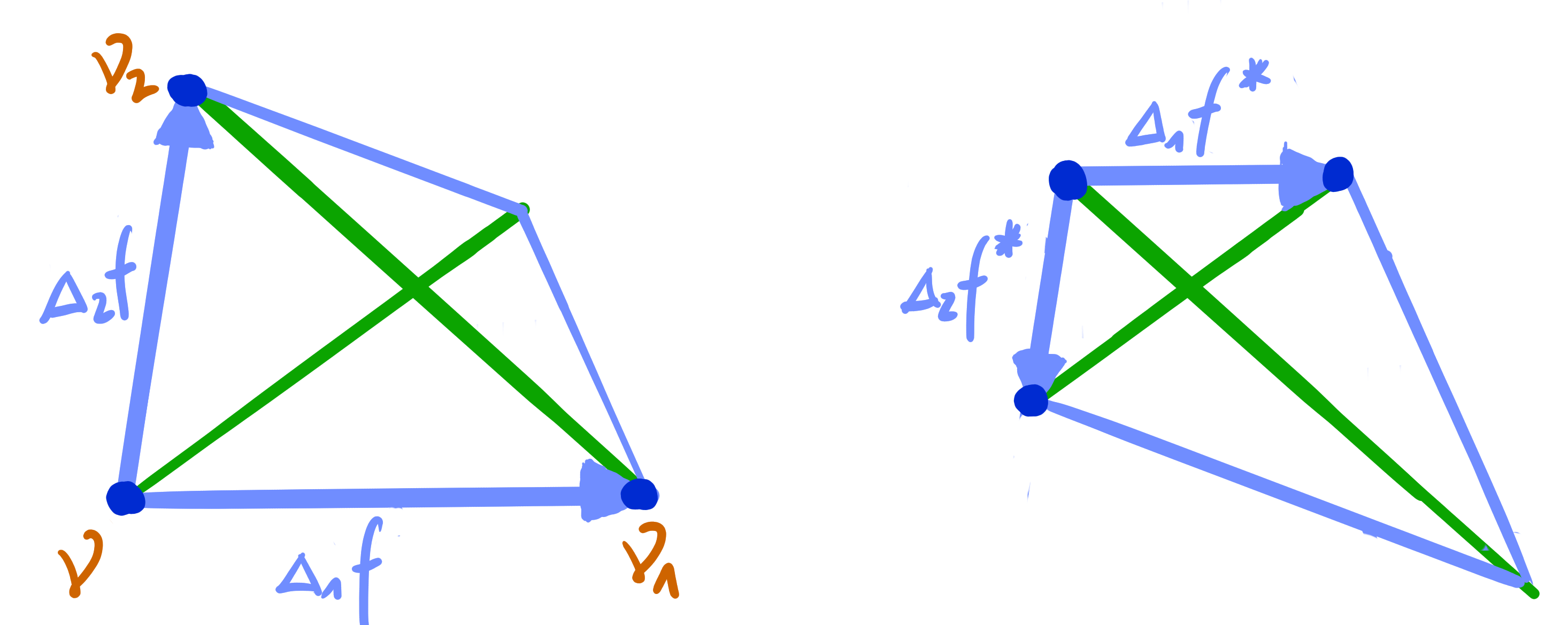
- Equivalently, dual quads have parallel corresponding edges and parallel non-corresponding diagonals.
Theorem:[Bobenko Suris 07]
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a BS-Christoffel dual if and only if $f$ is a BS-Kœnigs net.
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a BS-Christoffel dual if and only if $f$ is a BS-Kœnigs net.
Definition:
A D-Kœnigs net is a Q-net $~f : \Z^2 \rightarrow \R\mathrm{P}^n~$ such that
at every face the discrete Laplace invariants satisfy \[ H^1 \cdot H^2_1 \cdot H^1_2 \cdot H^2 = 1. \]
at every face the discrete Laplace invariants satisfy \[ H^1 \cdot H^2_1 \cdot H^1_2 \cdot H^2 = 1. \]
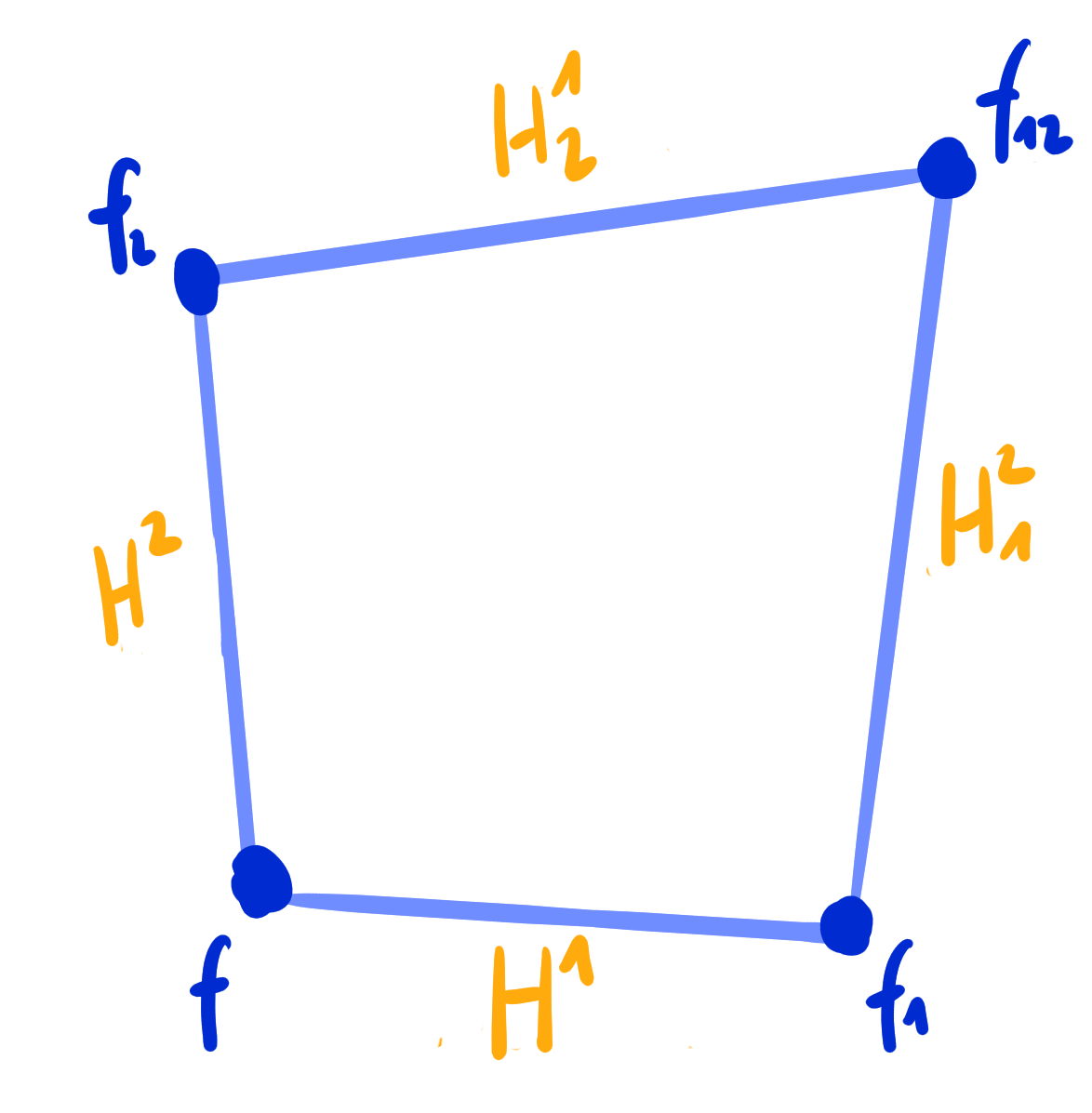
- Geometric characterization by conic through Laplace points.
- Algebraic characterization by homogeneous lift that satisfies a discrete "vertex based" Moutard equation.
Definition:
Let $f, f^* : \Z^2 \rightarrow \R^n \subset \R\mathrm{P}^n$ be two Q-nets.
Then $f^*$ is a D-Christoffel dual of $f$ if there exists $\nu : F(\Z^2) \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_{\bar 2}} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_{\bar 1}} \Delta_2 f \]
Then $f^*$ is a D-Christoffel dual of $f$ if there exists $\nu : F(\Z^2) \rightarrow \R \setminus \{0\}$ such that \[ \Delta_1 f^* = \frac{1}{\nu\nu_{\bar 2}} \Delta_1 f \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_{\bar 1}} \Delta_2 f \]
Theorem:[ADT24+]
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a D-Christoffel dual if and only if $f$ is a D-Kœnigs net.
A Q-net $~f : \Z^2 \rightarrow \R^n~$ has a D-Christoffel dual if and only if $f$ is a D-Kœnigs net.
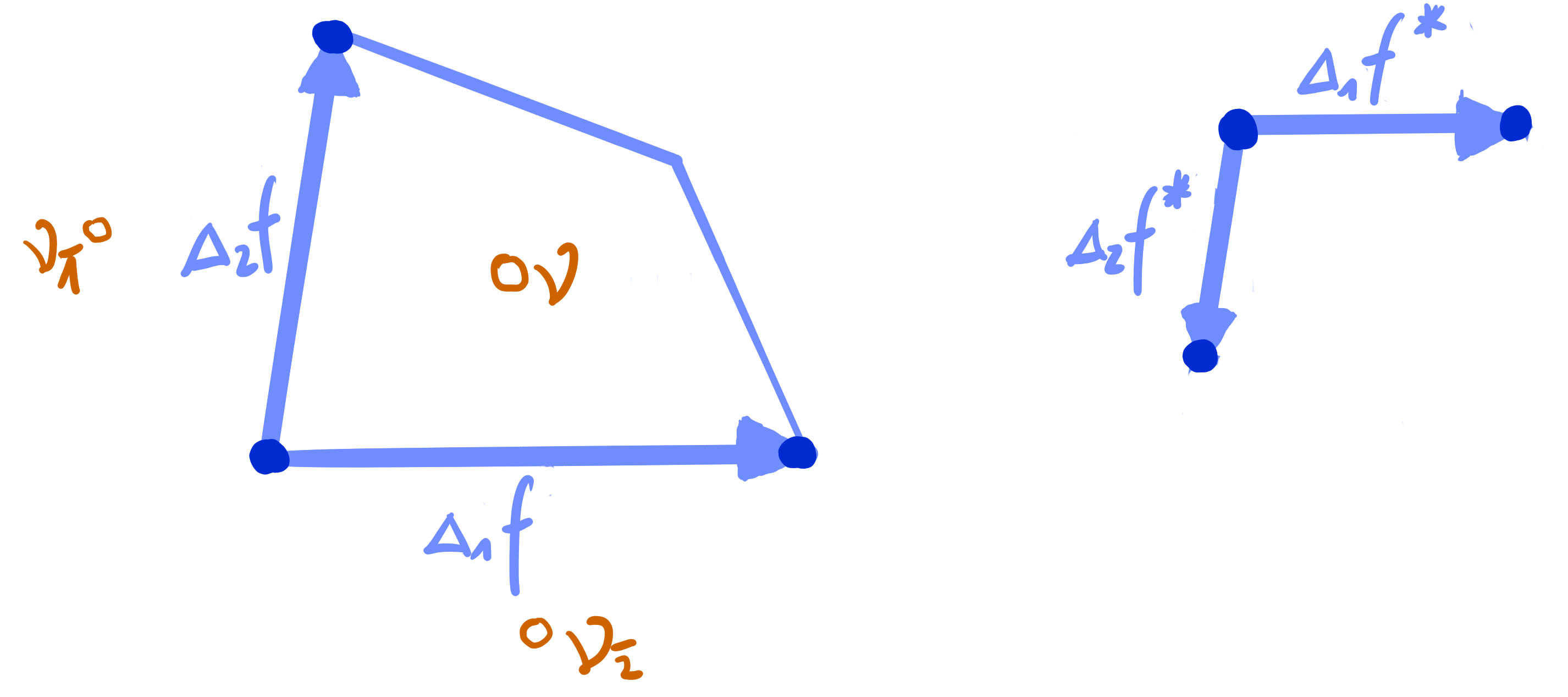
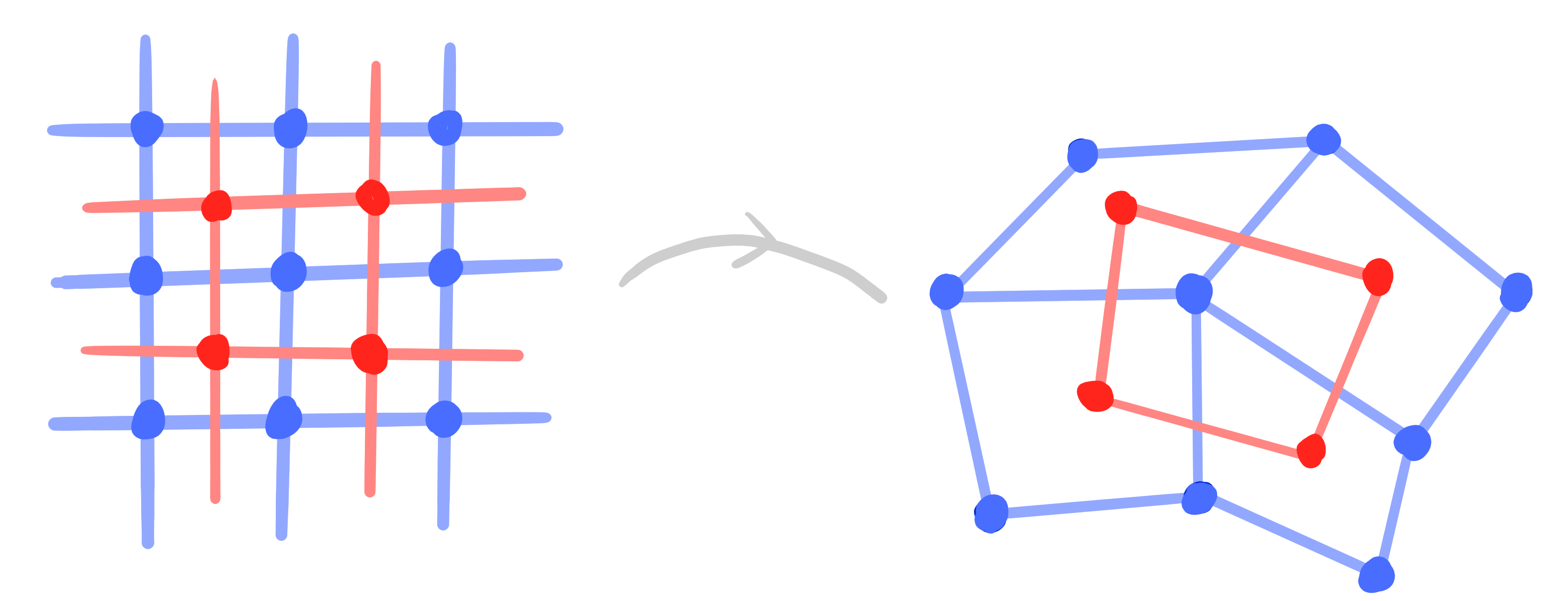
Theorem: [Bokenko Suris 07]
Let $~f : \Z^2 \rightarrow \R\mathrm{P}^n~$ be a BS-Kœnigs net.
Let $~g : F(\Z^2) \rightarrow \R\mathrm{P}^n$ be the net of diagonal intersection points of $f$.
Then $g$ is a D-Kœnigs net.
Let $~g : F(\Z^2) \rightarrow \R\mathrm{P}^n$ be the net of diagonal intersection points of $f$.
Then $g$ is a D-Kœnigs net.
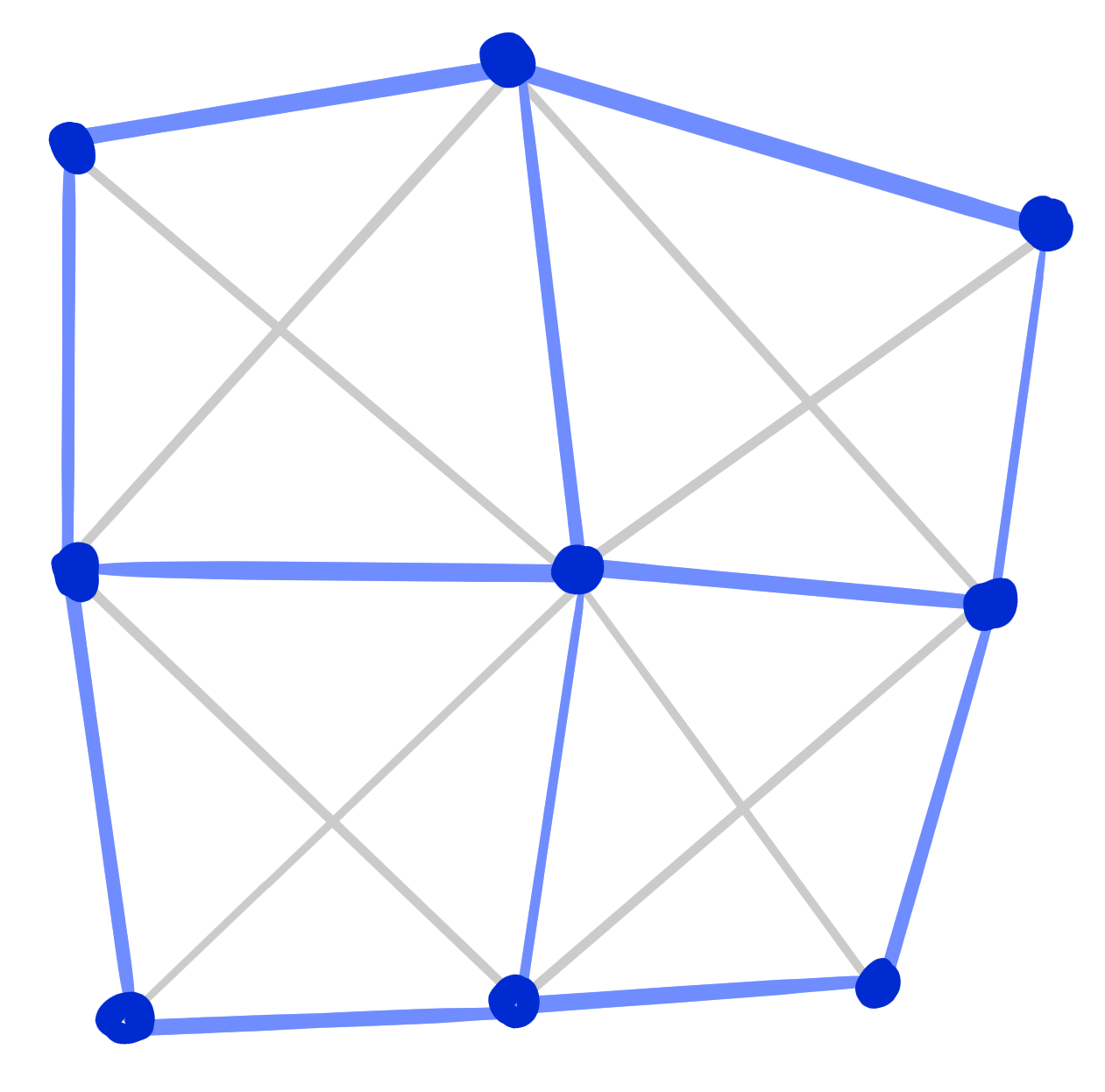
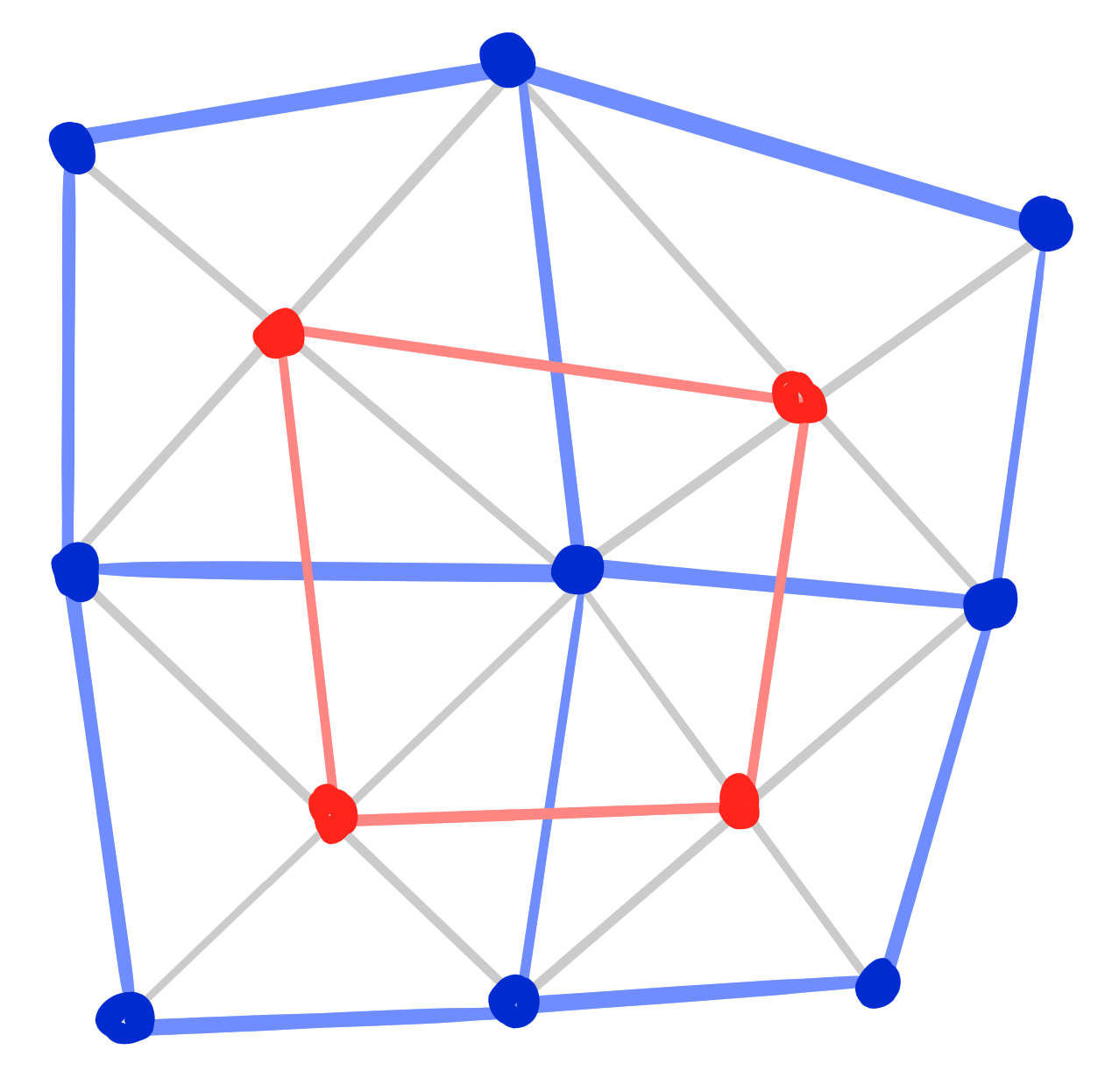
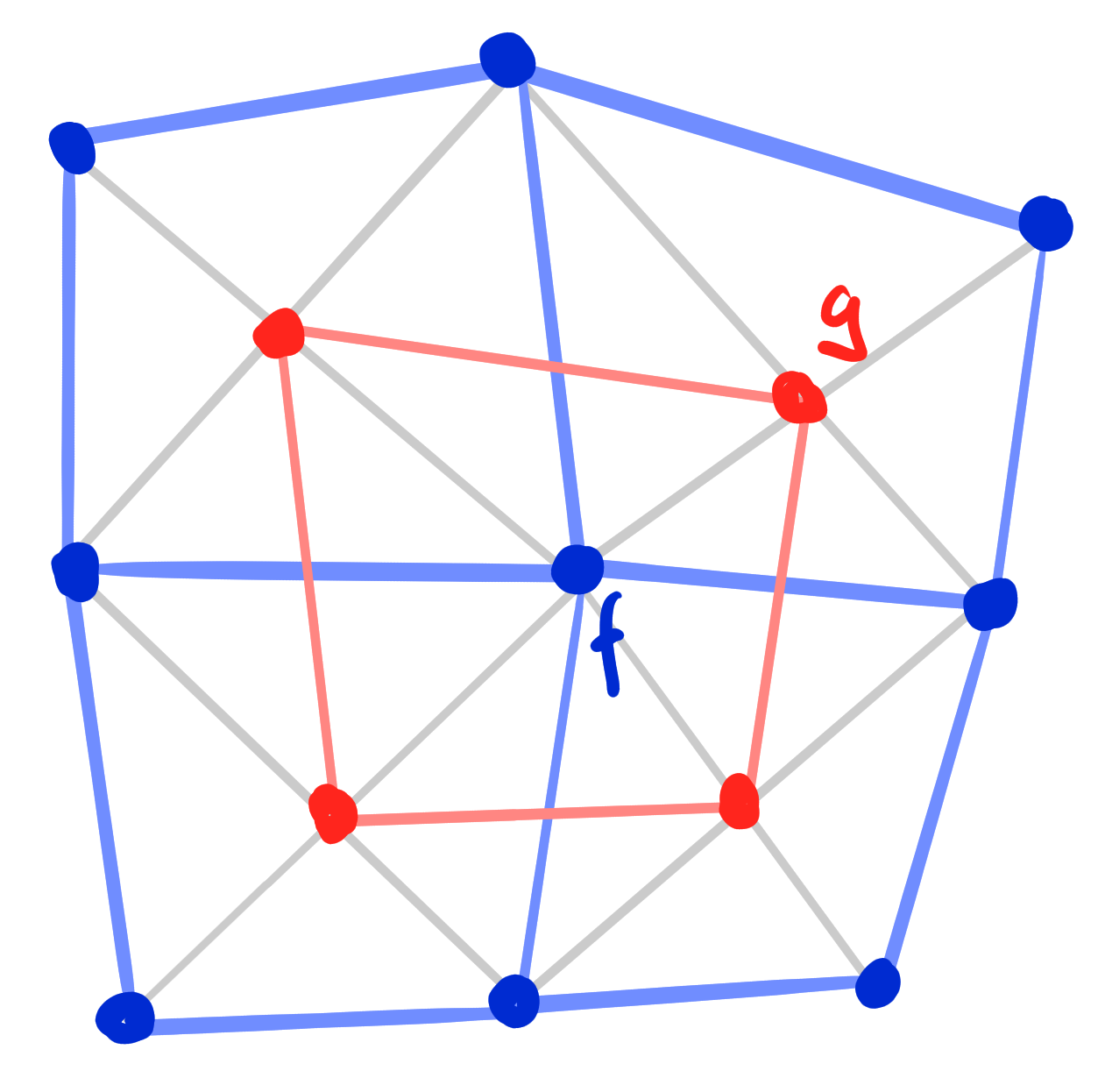
Remark: [Steinmeier 18]
The reverse construction is similarly possible (D-Kœnigs to BS-Kœnigs).
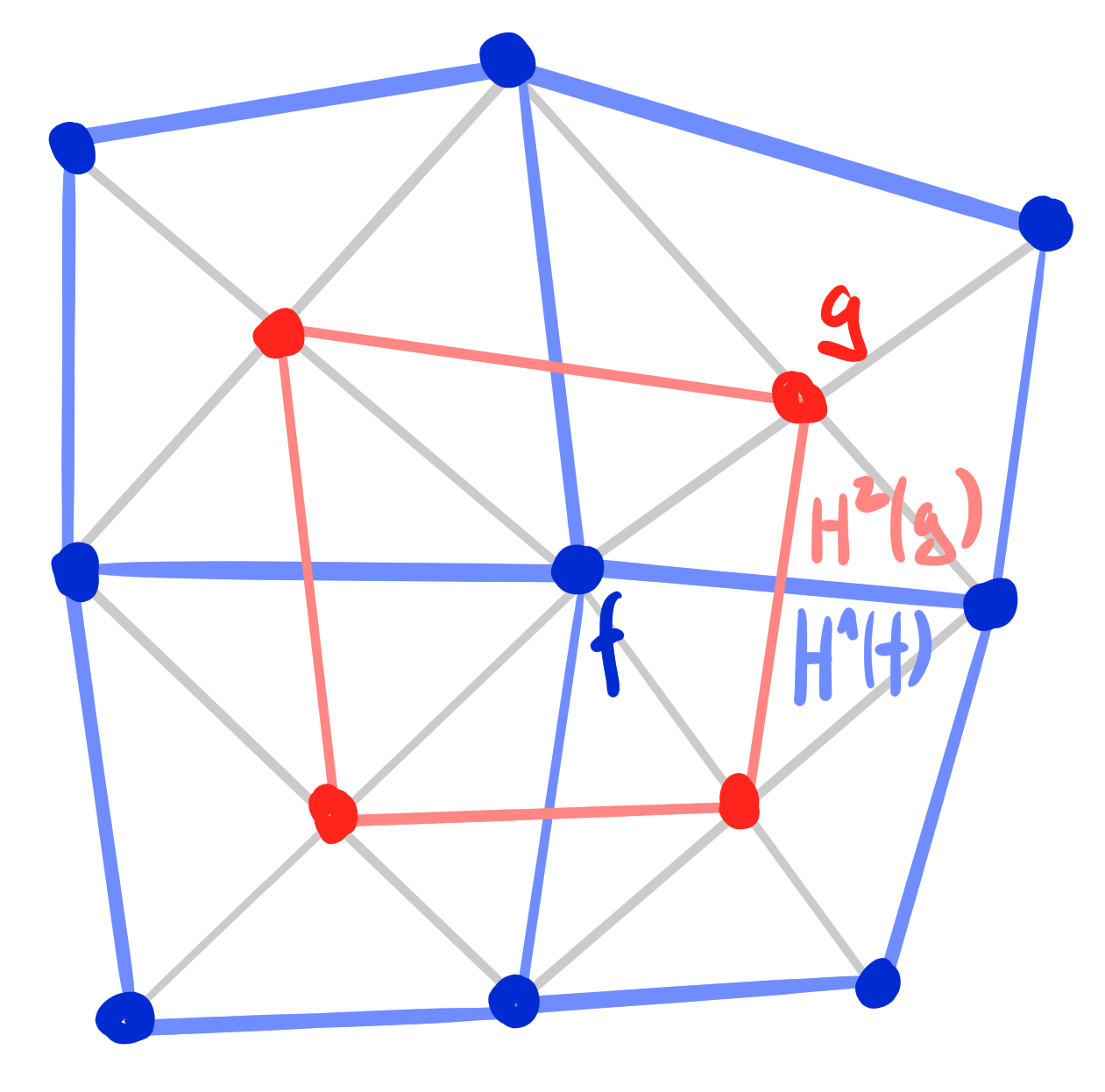
Theorem: [ADT24+]
The two discrete Laplace invariants on dual edges of $f$ and $g$ satisfy
\[
H^1(f) \cdot H^2(g) = 1, \qquad
H^2(f) \cdot H^1(g) = 1.
\]
Theorem: [ADT24+]
Let $~f : \Z^2 \rightarrow \R^n$ be a BS-Kœnigs net.
Let $~g : F(\Z^2) \rightarrow \R^n$ be the net of diagonal intersection points of $f$.
Let $\nu : \Z^2 \rightarrow \R\setminus\{0\}$ such that
$\qquad\qquad\qquad \Delta_1 f^* = \frac{1}{\nu\nu_1} \Delta_1 f, \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_2} \Delta_2 f $
is closed and $f^*$ is a BS-Christoffel dual of $f$.
Then
$\qquad\qquad\qquad \Delta_1 g^* = \frac{1}{\nu\nu_2} \Delta_1 g \qquad \Delta_2 g^* = -\frac{1}{\nu\nu_1} \Delta_2 g $
is closed and $g^*$ is a D-Christoffel dual of $g$.
Let $~g : F(\Z^2) \rightarrow \R^n$ be the net of diagonal intersection points of $f$.
Let $\nu : \Z^2 \rightarrow \R\setminus\{0\}$ such that
$\qquad\qquad\qquad \Delta_1 f^* = \frac{1}{\nu\nu_1} \Delta_1 f, \qquad \Delta_2 f^* = -\frac{1}{\nu\nu_2} \Delta_2 f $
is closed and $f^*$ is a BS-Christoffel dual of $f$.
Then
$\qquad\qquad\qquad \Delta_1 g^* = \frac{1}{\nu\nu_2} \Delta_1 g \qquad \Delta_2 g^* = -\frac{1}{\nu\nu_1} \Delta_2 g $
is closed and $g^*$ is a D-Christoffel dual of $g$.
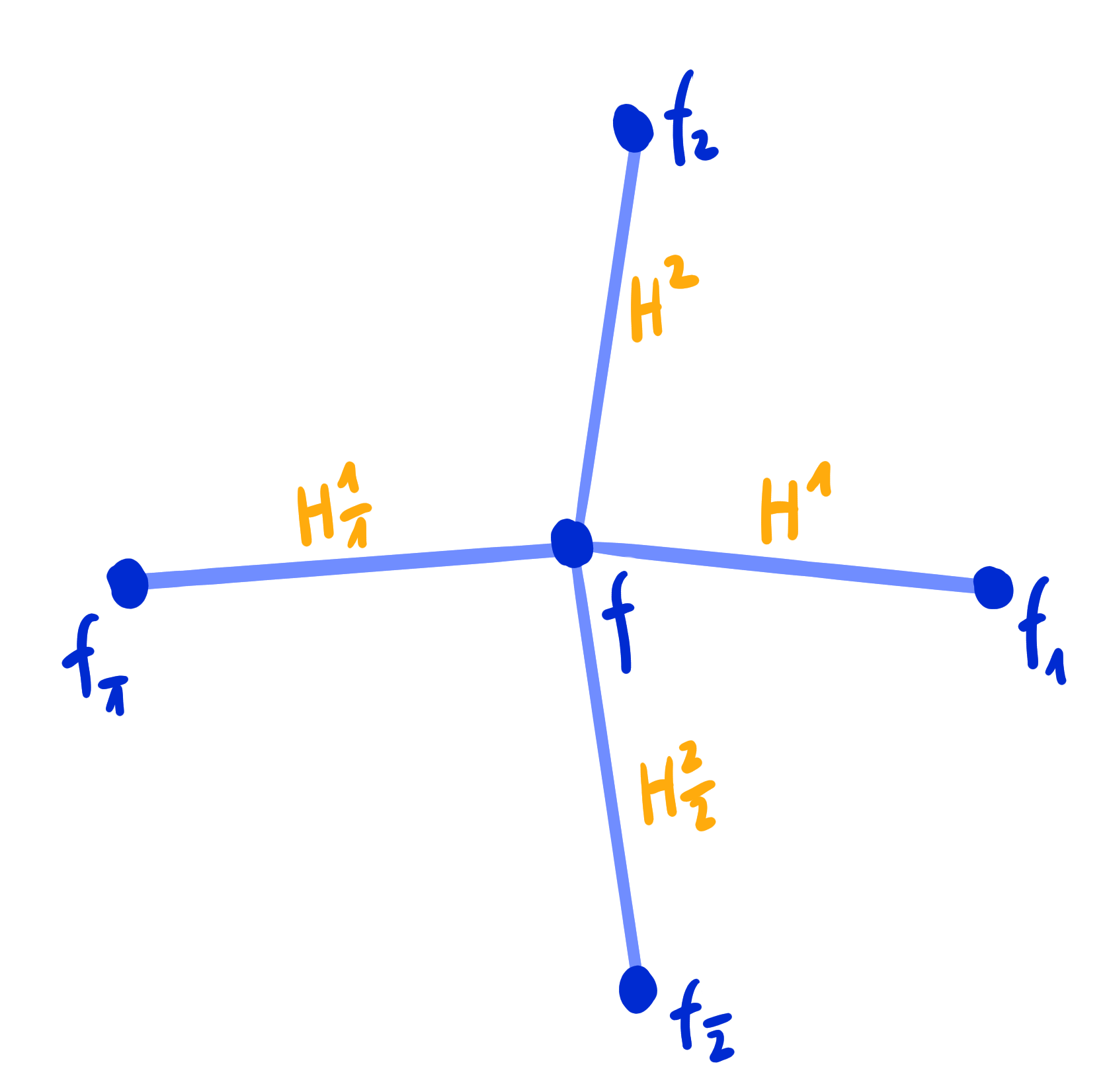
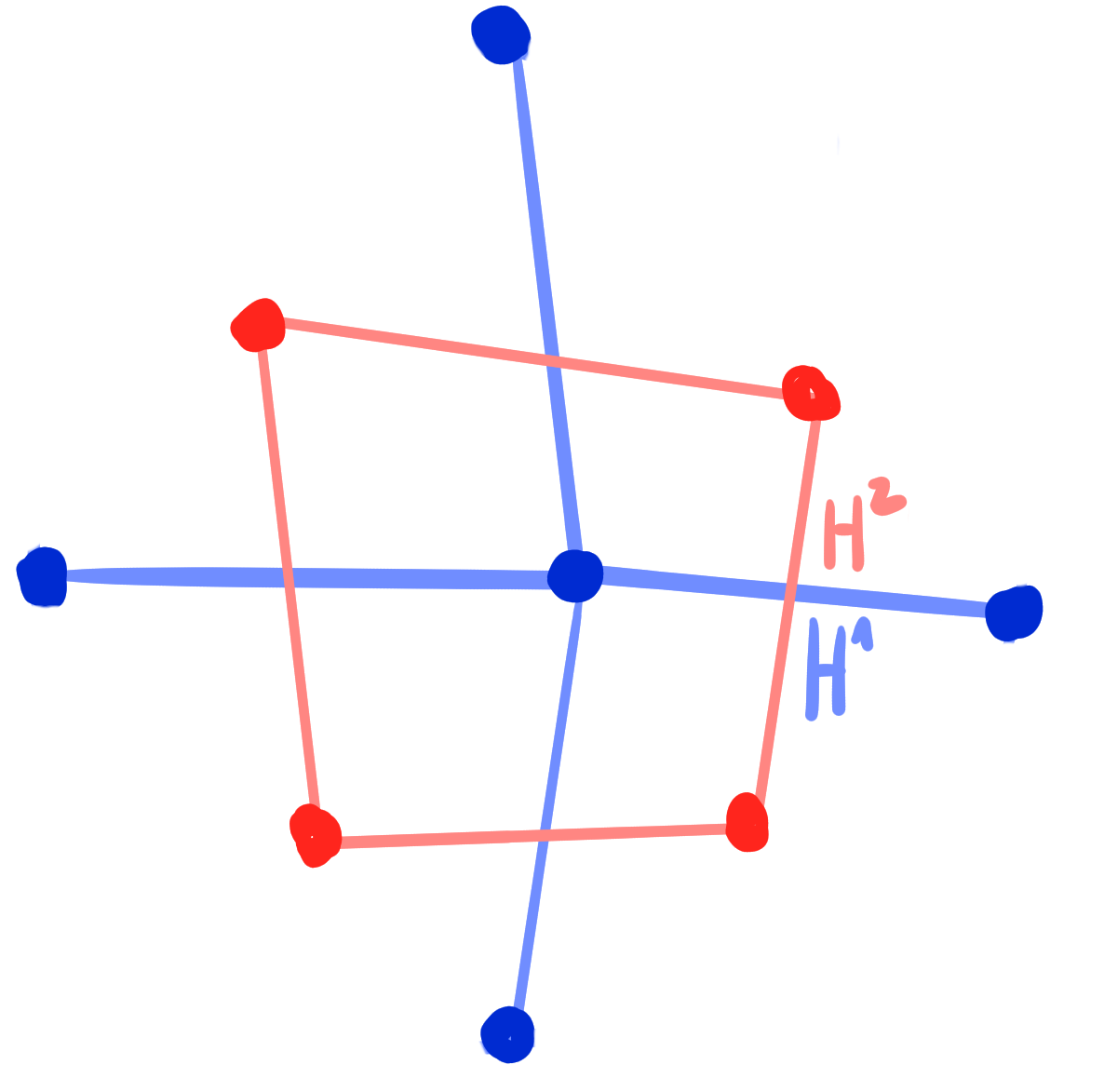
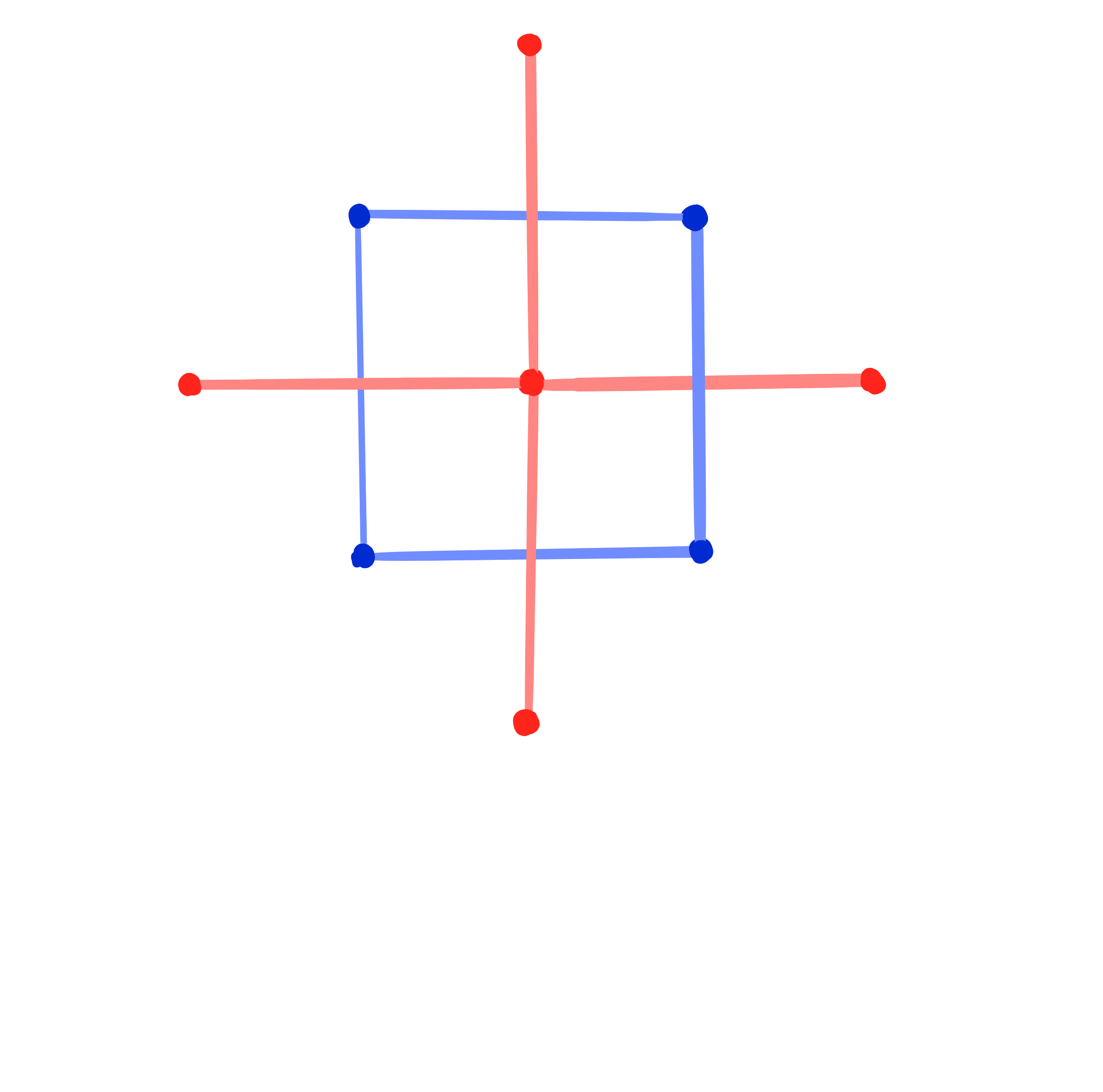
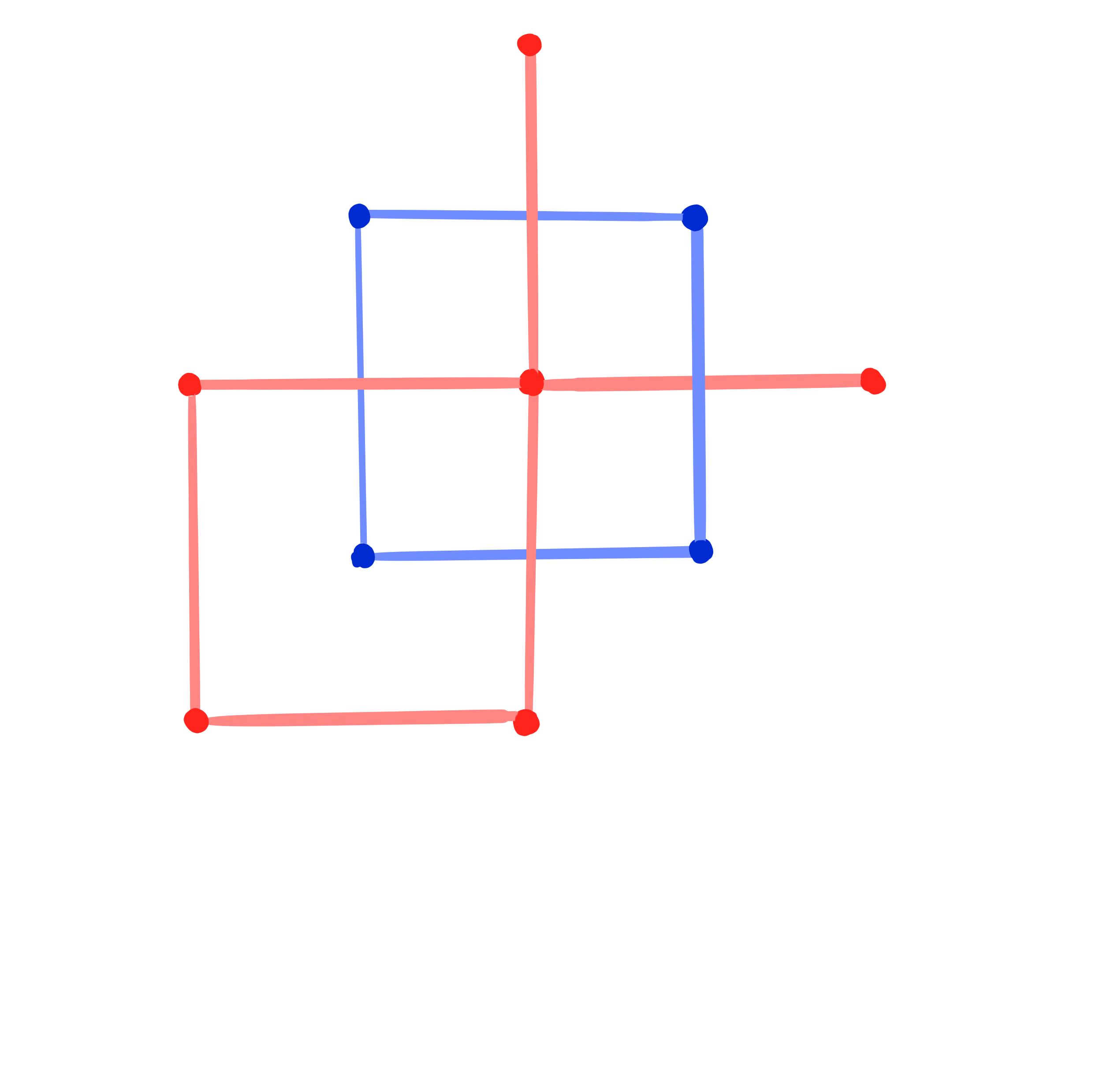
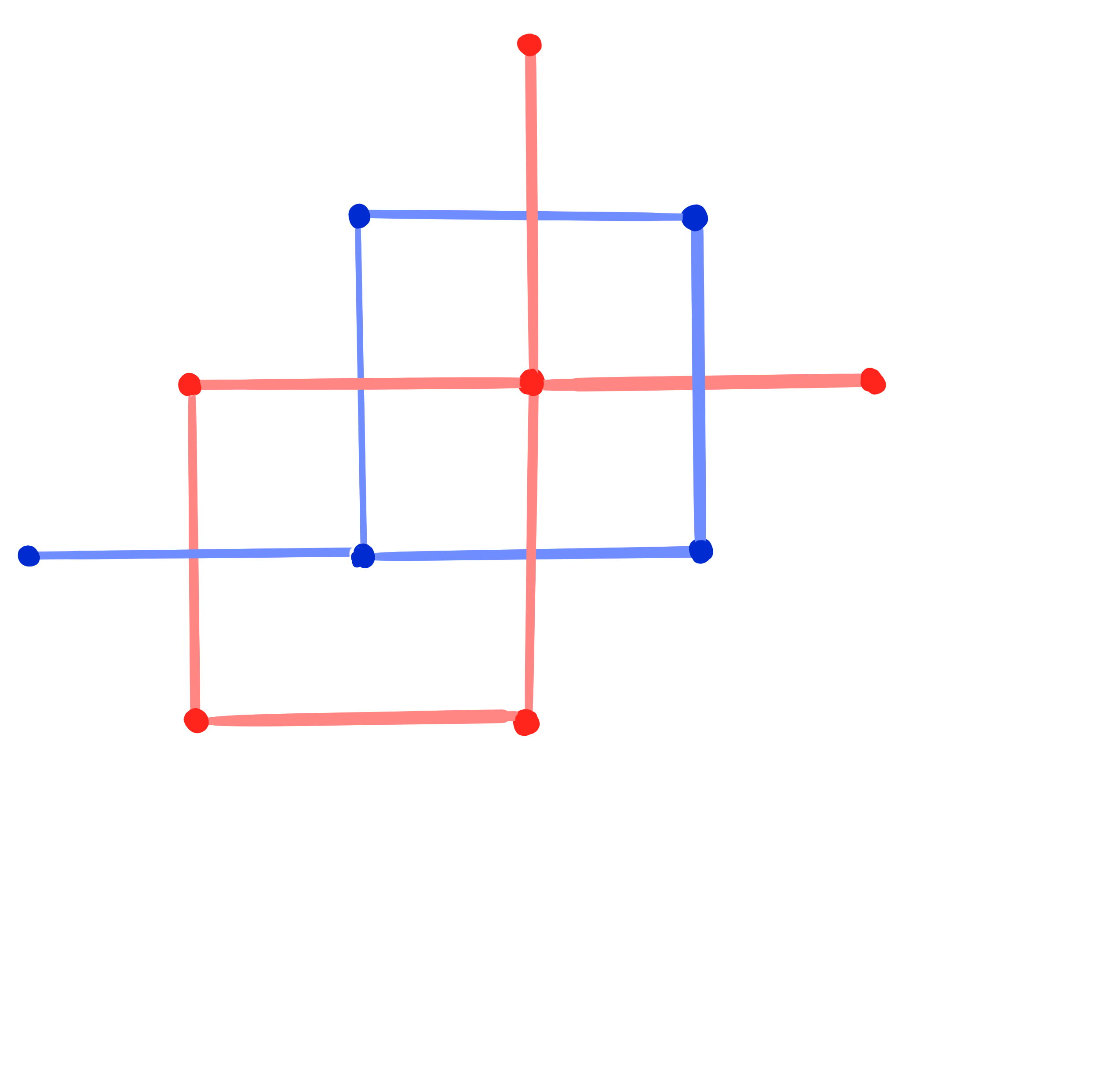
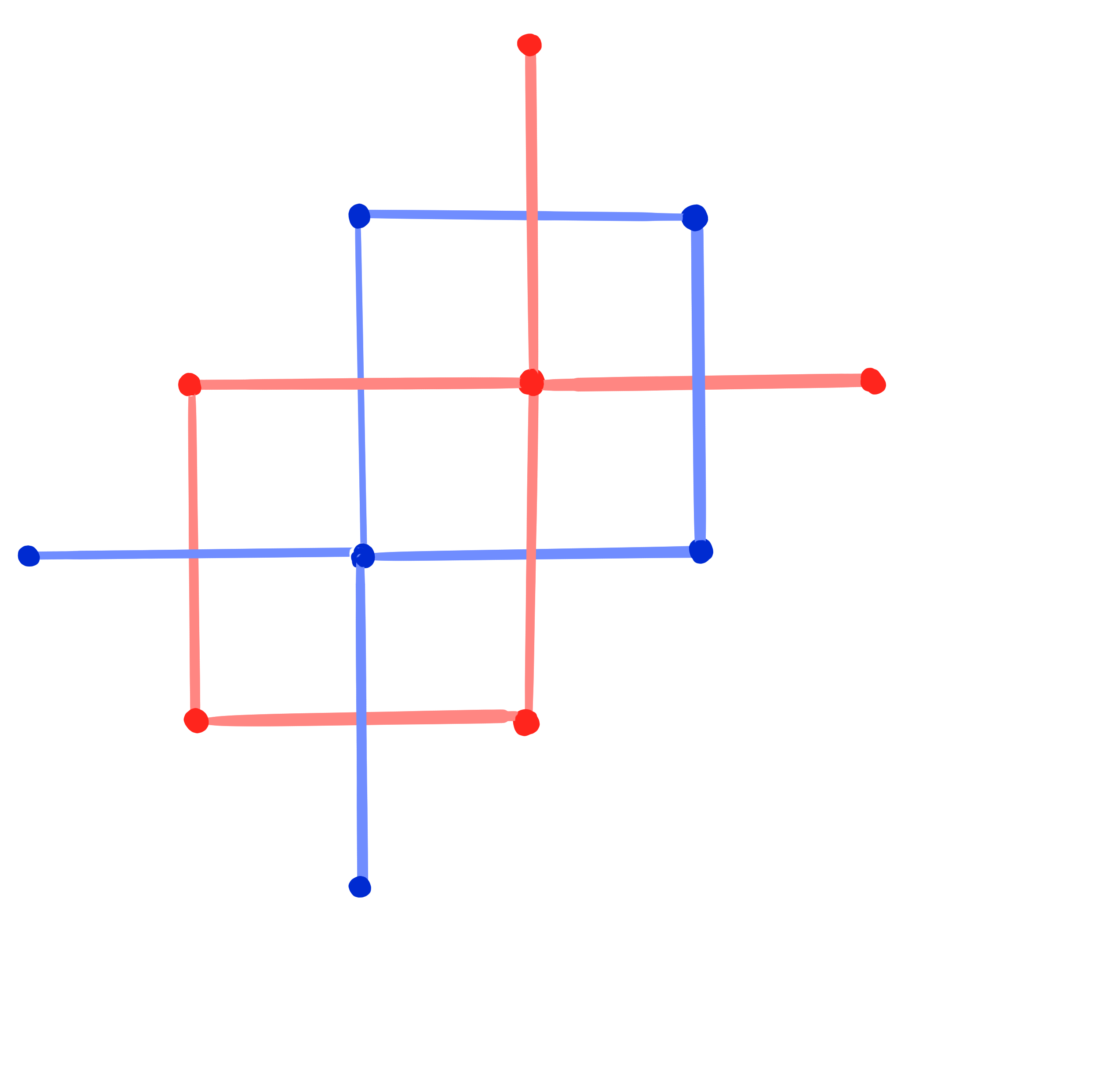
Definition:
A binet is a map
$b : \Z^2 \cup F(\Z^2) \rightarrow \R\mathrm{P}^n$.
Definition:
A conjugate binet is a binet $b$ such that
$b|_{\Z^2}$ and $b|_{F(\Z^2)}$ are Q-nets.
$b|_{\Z^2}$ and $b|_{F(\Z^2)}$ are Q-nets.
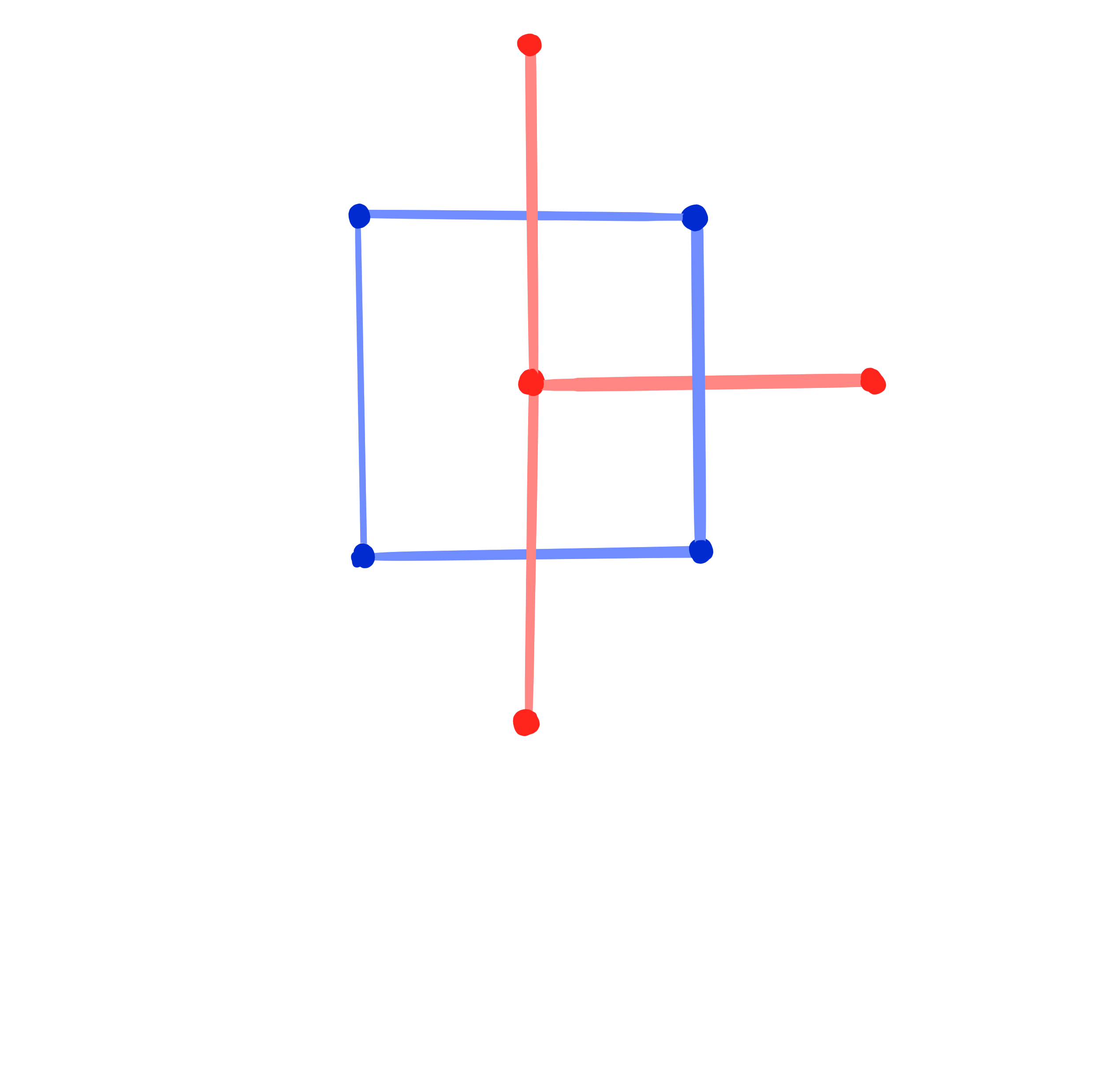
Definition:
A Kœnigs binet is a conjugate binet $~b : \Z^2 \cup F(\Z^2) \rightarrow \R\mathrm{P}^n~$such that
at every cross (edge and dual edge) the Laplace invariants satisfy \[ H^1 \cdot H^2 = 1. \]
at every cross (edge and dual edge) the Laplace invariants satisfy \[ H^1 \cdot H^2 = 1. \]
Example:
Pairs of BS-Kœnigs nets and D-Kœnigs nets.
Theorem: [ADT24+]
Let $~ b : \Z^2 \cup F(\Z^2) \rightarrow \R\mathrm{P}^n~$ be a Kœnigs binet.
Then $b|_{\Z^2}$ is a BS-Kœnigs net $~\Leftrightarrow~$ $b|_{F(\Z^2)}$ is a D-Kœnigs.
Then $b|_{\Z^2}$ is a BS-Kœnigs net $~\Leftrightarrow~$ $b|_{F(\Z^2)}$ is a D-Kœnigs.
Theorems: [Affolter Fairley 24+]
On Laplace sequences...
Definition:
Let $~b, b^* : \Z^2 \cup F(\Z^2) \rightarrow \R^n ~$ be two conjugate binets.
Then $b^*$ is called Christoffel dual binet of $b$ if there exists $~\nu : E(\Z^2) \rightarrow \R\setminus \{0\} ~$ such that
\[ \Delta_1 b^* = \frac{1}{\nu^2} \Delta_1 b,\qquad \Delta_2 b^* = -\frac{1}{\nu^2} \Delta_2 b \] at every cross (pair of edge and dual edge).
Then $b^*$ is called Christoffel dual binet of $b$ if there exists $~\nu : E(\Z^2) \rightarrow \R\setminus \{0\} ~$ such that
\[ \Delta_1 b^* = \frac{1}{\nu^2} \Delta_1 b,\qquad \Delta_2 b^* = -\frac{1}{\nu^2} \Delta_2 b \] at every cross (pair of edge and dual edge).
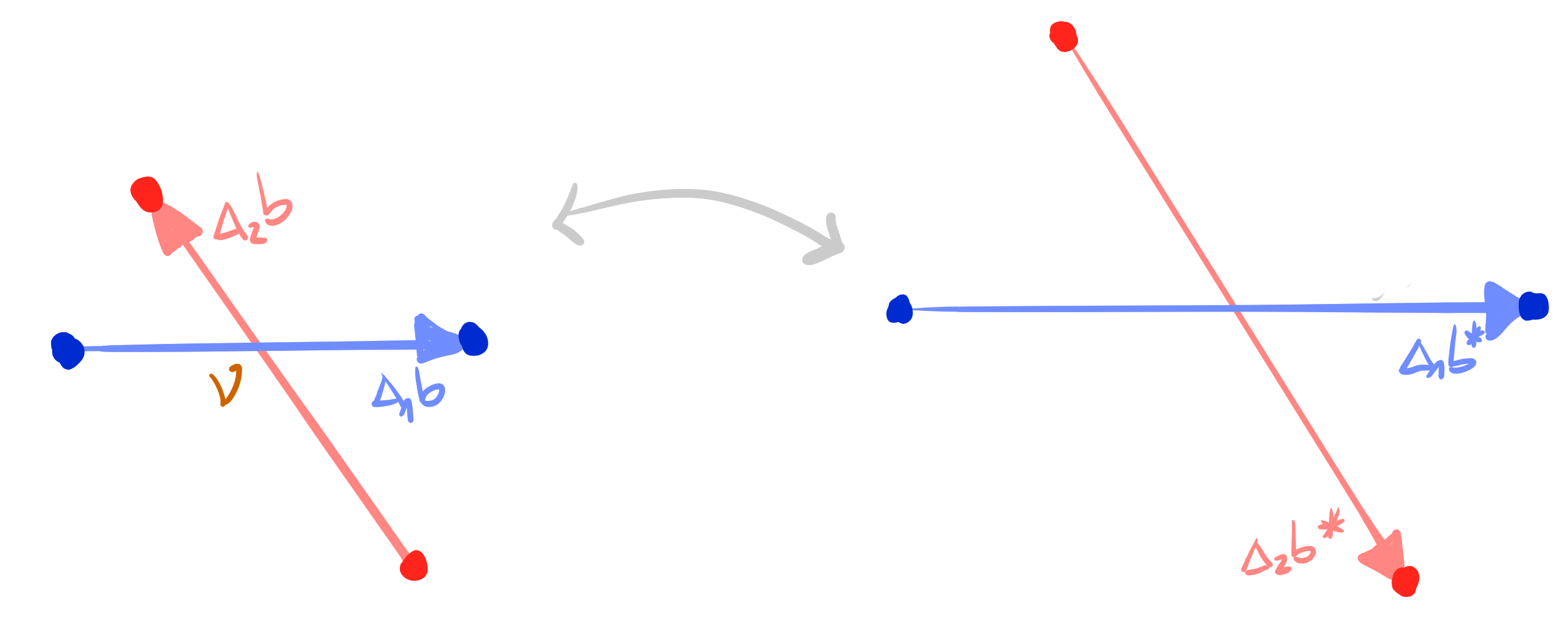
Closing condition for Christoffel dual binet
$
\Leftrightarrow\quad H^1 \cdot H^2 = 1.
$
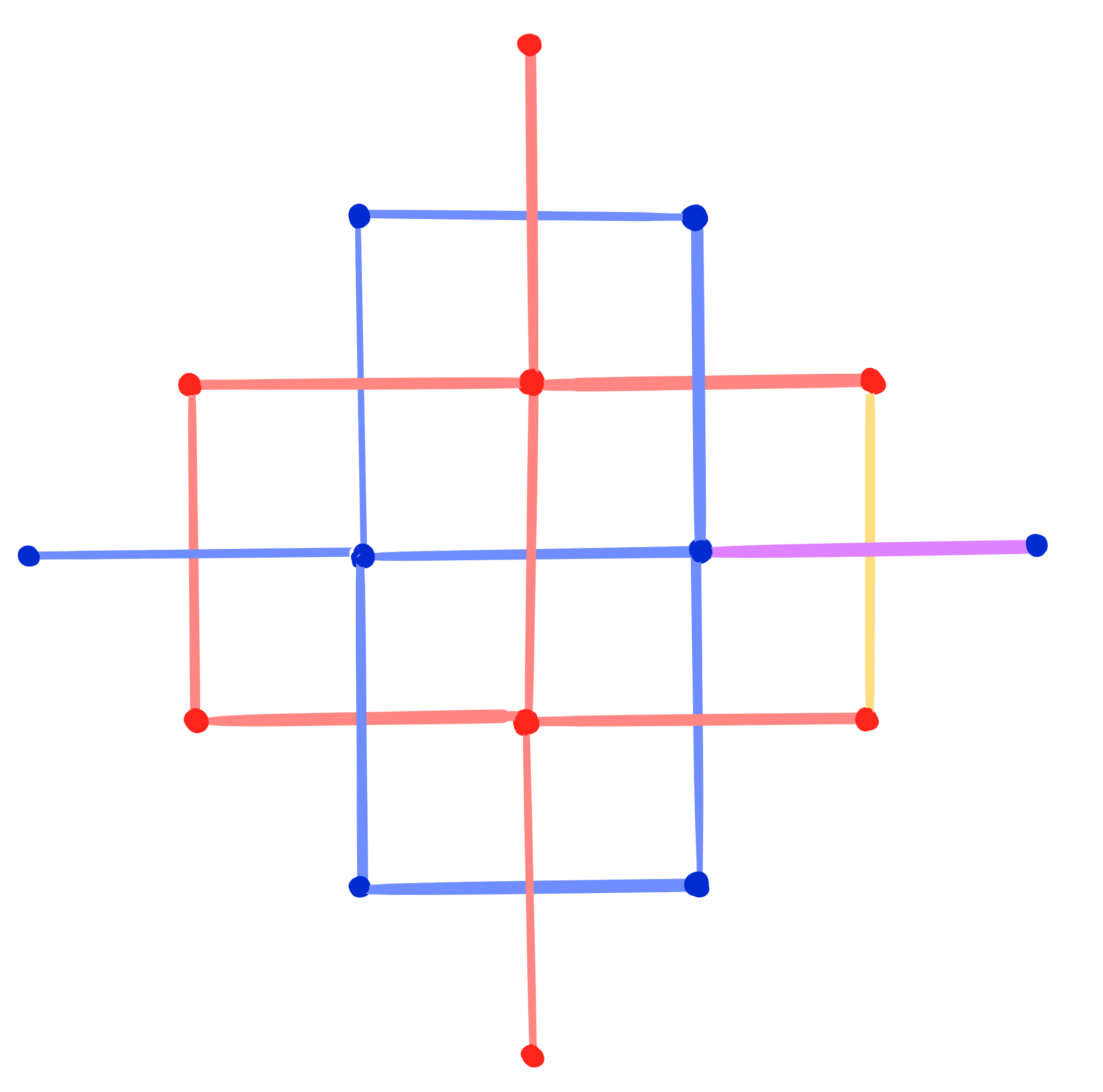
Theorem: [Dellinger 22, ADT24+]
A conjugate binet $b$ has a Christoffel dual binet if and only if $b$ is a Kœnigs binet.
A conjugate binet $b$ has a Christoffel dual binet if and only if $b$ is a Kœnigs binet.
Definition:
A ($m$-dimensional) discrete net is a map $~ f: \Z^m \rightarrow \R\mathrm{P}^n$.
A discrete conjugate net (Q-net) is a discrete net
such that for each face the four points lie in a plane.
A ($m$-dimensional) discrete net is a map $~ f: \Z^m \rightarrow \R\mathrm{P}^n$.
A discrete conjugate net (Q-net) is a discrete net
such that for each face the four points lie in a plane.





Theorem: [Doliwa Santini 97]
Q-nets are multi-dimensionally consistent 3D-systems.
Q-nets are multi-dimensionally consistent 3D-systems.
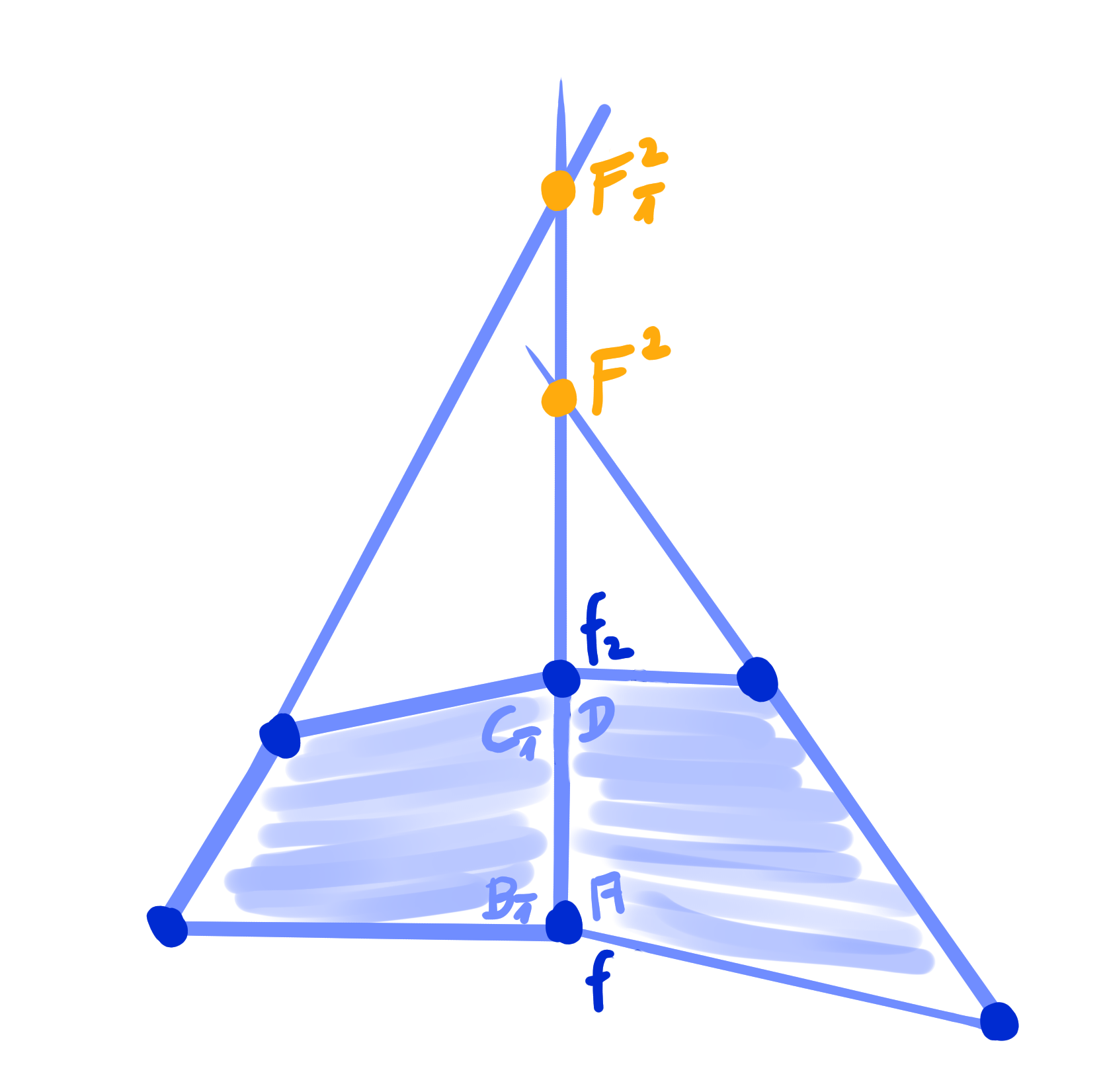
Definition:
The Laplace invariants of a Q-net $~f : \Z^m \rightarrow \R\mathrm{P}^n~$ are
| \[ H^{ijk}(f) = - \mathrm{cr}(f, A^{ij}, f_i, A^{ik}). \] |
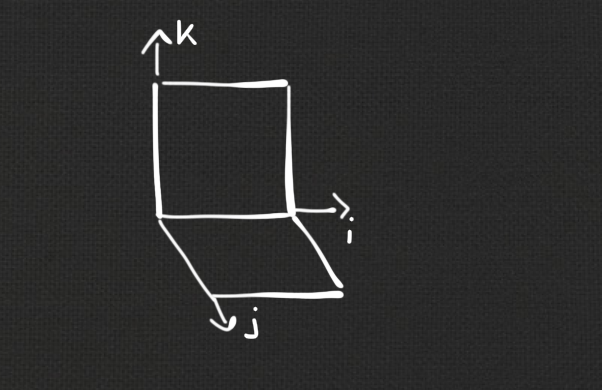
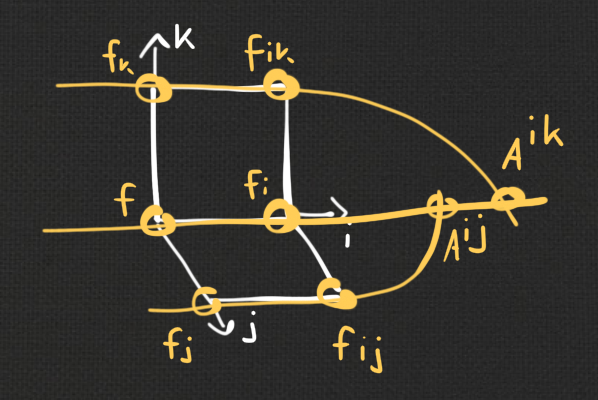
|
Definition:
A BS-Kœnigs net is a Q-net such that the Laplace invariants satisfy $$H^{ijk} \cdot H^{jki} \cdot H^{kij} = 1.$$
A BS-Kœnigs net is a Q-net such that the Laplace invariants satisfy $$H^{ijk} \cdot H^{jki} \cdot H^{kij} = 1.$$
- On all $\Z^2 \subset \Z^m$ this coicides with the previous definition of BS-Kœnigs nets on $\Z^2$.
Theorem:[Bobenko Suris 07]
BS-Kœnigs nets are a consistent reduction of Q-nets.
BS-Kœnigs nets are a consistent reduction of Q-nets.
Definition:
A ($m$-dimensional) face-net is a map $~ g: F(\Z^m) \rightarrow \R\mathrm{P}^n$.
A line compound (Q-net) is a face-net
such that for each 3D-cube the six points lie on a line.
A ($m$-dimensional) face-net is a map $~ g: F(\Z^m) \rightarrow \R\mathrm{P}^n$.
A line compound (Q-net) is a face-net
such that for each 3D-cube the six points lie on a line.
- On all $\Z^2 \subset \Z^m$ a line compound is a $2$-dimensional Q-net on $F(\Z^2)$.
-
$~m=3~$: the lines of a line compound can be identified with a line complex
[Bobenko Suris 15]
$~m>3~$: this identification does not hold.
Theorem: [ADT24+]
Line compounds are multi-dimensionally consistent 3D-systems.
Line compounds are multi-dimensionally consistent 3D-systems.
Definition:
The Laplace invariants of a line compound $~g : F(\Z^m) \rightarrow \R\mathrm{P}^n~$ are
| \[ H^{ijk}(g) = - \mathrm{cr}(g^{jk}, g^{ij}, g_i^{jk}, g^{ik}). \] |
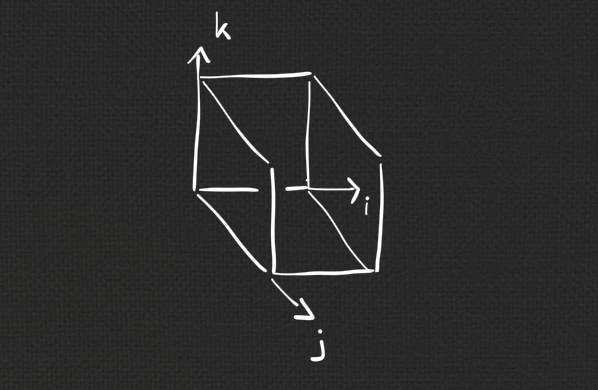
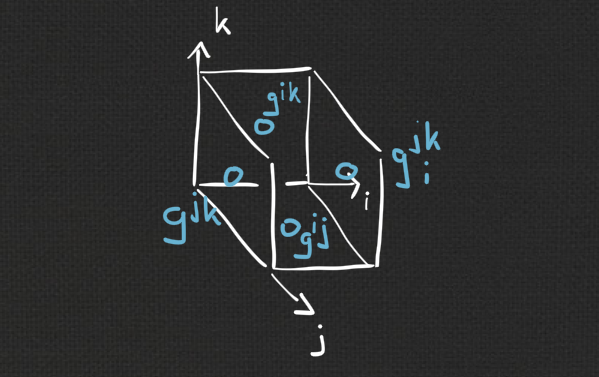
|
Definition:
A ($m$-dimensional) D-Kœnigs net is a line compound such that the Laplace invariants satisfy $$H^{ijk} \cdot H^{jki} \cdot H^{kij} = 1.$$
A ($m$-dimensional) D-Kœnigs net is a line compound such that the Laplace invariants satisfy $$H^{ijk} \cdot H^{jki} \cdot H^{kij} = 1.$$
- On all $\Z^2 \subset \Z^m$ this coicides with the previous definition of D-Kœnigs nets on $\Z^2$.
Theorem:[ADT24+]
D-Kœnigs nets are a consistent reduction of line compounds.
D-Kœnigs nets are a consistent reduction of line compounds.
Definition:
A ($m$-dimensional) binet is a map $~b : \Z^m \cap F(\Z^m) \rightarrow \R\mathrm{P}^n$.
A ($m$-dimensional) conjugate binet is a binet $b$ such that
$b|_{\Z^m}$ is a Q-net, and $b|_{F(\Z^m)}$ is a line compound.
A ($m$-dimensional) binet is a map $~b : \Z^m \cap F(\Z^m) \rightarrow \R\mathrm{P}^n$.
A ($m$-dimensional) conjugate binet is a binet $b$ such that
$b|_{\Z^m}$ is a Q-net, and $b|_{F(\Z^m)}$ is a line compound.
- On all $\Z^2 \subset \Z^m$ this coicides with the previous definition of conjugate binets on $\Z^2$.
Corollary: [ADT24+]
Conjugate binets are multi-dimensionally consistent 3D-systems.
Conjugate binets are multi-dimensionally consistent 3D-systems.
Definition:
AKœnigs binet is a conjugate binet such that for every edge the Laplace invariants
of the Q-net $f = b|_{\Z^m}$ and the Laplace invariants of the line compound $g = b|_{F(\Z^m)}$ satsify
\[
H^{ijk}(f) \cdot H^{ijk}(g) = 1
\]
A
Example:
Pairs of BS-Kœnigs nets and D-Kœnigs nets.
Theorem: [ADT24+]
Let $~ b : \Z^m \cup F(\Z^m) \rightarrow \R\mathrm{P}^n~$ be a Kœnigs binet.
If its restriction $b|_{\Z^m}$ is a BS-Kœnigs net, then its restriction $b|_{F(\Z^m)}$ is a D-Kœnigs net,
and vice versa.
Let $~ b : \Z^m \cup F(\Z^m) \rightarrow \R\mathrm{P}^n~$ be a Kœnigs binet.
If its restriction $b|_{\Z^m}$ is a BS-Kœnigs net, then its restriction $b|_{F(\Z^m)}$ is a D-Kœnigs net,
and vice versa.
Theorem:[ADT24+]
Kœnigs binets are a consistent reduction of conjugate binets.
Kœnigs binets are a consistent reduction of conjugate binets.
Similar theory for principal binets[AT24]
- conjugate binets with orthogonality constraint
- generalization of pairs of circular and conical nets
- lift to Möbius, Laguerre, Lie geometry
- multi-dimensional consistency (uses different generalization of conjugate binets to $\Z^m$)
WIP: isothermic binets
- combine principal binets with Kœnigs binets
- example: S-conical nets
- multi-dimensional consistency?

Thank you!
Theorem:
Kœnigs binets are a consistent reduction of conjugate binets.
[ADT24+]
Kœnigs binets are a consistent reduction of conjugate binets.
Sketch of proof:
The Laplace invariants of both Q-nets and line compounds satisfy $$ H^{i\bar j\bar k}_{jk} = \frac{1+H^{ijk}(1+H_i^{kj\bar i})}{H_i^{kj\bar i}(1+H_i^{j \bar i k}(1+H^{ijk}))}, \quad H^{kj\bar i} = H^{k\bar j i}H^{k \bar i j}(1+H^{ijk}(1+H_i^{kj\bar i})). $$ These two formulas suffice to calculate all Laplace invariants from initial data.$\square$
The Laplace invariants of both Q-nets and line compounds satisfy $$ H^{i\bar j\bar k}_{jk} = \frac{1+H^{ijk}(1+H_i^{kj\bar i})}{H_i^{kj\bar i}(1+H_i^{j \bar i k}(1+H^{ijk}))}, \quad H^{kj\bar i} = H^{k\bar j i}H^{k \bar i j}(1+H^{ijk}(1+H_i^{kj\bar i})). $$ These two formulas suffice to calculate all Laplace invariants from initial data.
Definition:
A ($2$-dimensional) net is a smooth map
$~ [\hat f] : \R^2 \supset U \rightarrow \R\mathrm{P}^n$.
- $2$-dimensional net $~=~$ parametrized surface
- $\hat f : U \rightarrow \R^{n+1}~$ is the homogeneous coordinate lift of $~[\hat f]$
- $[\hat f] = [\lambda \hat f]~$ for any $~\lambda : U \rightarrow \R \setminus \{0\}$
Definition:
A net $~[\hat f] : \R^2 \supset U \rightarrow \R\mathrm{P}^n~$ is a conjugate net
\[
\begin{aligned}
:\Leftrightarrow \quad &[\hat f_{uv}], [\hat f_u], [\hat f_v], [\hat f] ~~\text{lie in a plane}\\
\Leftrightarrow \quad &\hat f_{uv} + a \hat f_u + b \hat f_v + c \hat f = 0 ~~\text{with some}~~ a, b, c : U \rightarrow \R
\quad\text{(Laplace equation)}
\end{aligned}
\]
Conjugate nets are invariant under
- a change of the homogeneous lift (the coefficients $a, b, c$ change),
- projective transformations of $\R\mathrm{P}^n$.
Definition:
Let
$~ [\hat f] : \R^2 \supset U \rightarrow \R\mathrm{P}^n ~$
be a conjugate net with
\[
\hat f_{uv} + a \hat f_u + b \hat f_v + c \hat f = 0.
\]
Then the following quantities are called the Laplace invariants of $[\hat f]$.
\[ h := a_u + ab - c, \qquad k := b_v + ab - c. \]
\[ h := a_u + ab - c, \qquad k := b_v + ab - c. \]
The Laplace invariants are invariant under
- a change of the homogeneous lift,
- projective transformations of $\R\mathrm{P}^n$.
Definition:
Let
$~ [\hat f] : \R^2 \supset U \rightarrow \R P^n ~$ be a conjugate net.
Then $[\hat f]$ is called a Kœnigs net (or net with equal Laplace invariants) if \[ h = k \quad(\Leftrightarrow a_u = b_v). \]
Then $[\hat f]$ is called a Kœnigs net (or net with equal Laplace invariants) if \[ h = k \quad(\Leftrightarrow a_u = b_v). \]
Definition:
Let
$~ f, f^* : \R^2 \supset U \rightarrow \R^n \subset \R P^n ~$ be conjugate nets.
Then $f^*$ is called a Christoffel dual of $f$ if there exists $~\nu : U \rightarrow \R \setminus \{0\}~$ such that \[ f^*_u = \frac{1}{\nu^2} f_u,\qquad f^*_v = -\frac{1}{\nu^2} f_v. \]
Then $f^*$ is called a Christoffel dual of $f$ if there exists $~\nu : U \rightarrow \R \setminus \{0\}~$ such that \[ f^*_u = \frac{1}{\nu^2} f_u,\qquad f^*_v = -\frac{1}{\nu^2} f_v. \]
- The Christoffel dual is unique up to scaling and translation.
- Christoffel duality is invariant under affine transformations.
Theorem:
A conjugate net
$~ f : \R^2 \supset U \rightarrow \R^n~$
has a Christoffel dual
if and only if $f$ is a Kœnigs net.
if and only if $f$ is a Kœnigs net.
- The existence of a Christoffel dual is projectively invariant.