Geometry and consistency of principal binets



Jan Techter

joint work with Niklas Affolter [AT23+]



Part 1: Geometry

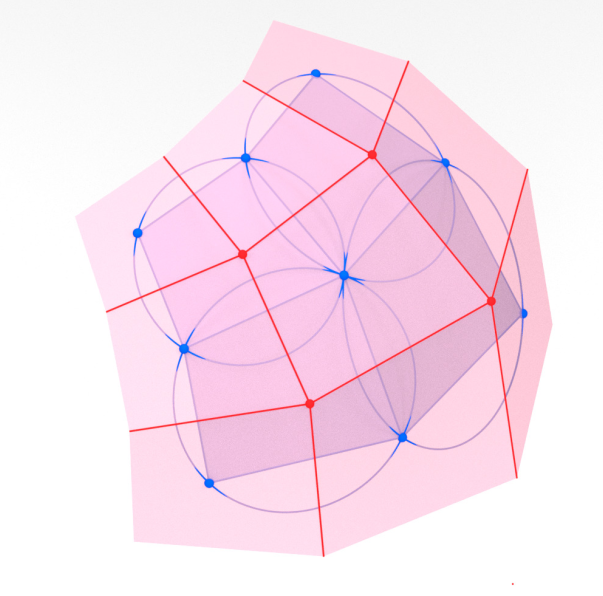
Examples: Discrete surfaces arising as pairs of combinatorially dual nets
Orthogonal circle patterns, Koebe polyhedra, and discrete minimal surfaces
  • [BHS08] Minimal surfaces from circle patterns: Geometry from combinatorics
    Bobenko, Hoffmann, Springborn.
Orthogonal ring patterns, generalized Koebe polyhedra, and discrete CMC surfaces
  • [BHR19] Orthogonal ring patterns
    Bobenko, Hoffmann, Rörig.
  • [BHS23+] Constant mean curvature surfaces from ring patterns: Geometry from combinatorics
    Bobenko, Hoffmann, Smeenk.
Circular nets and conical nets
  • [BS07] On organizing principles of Discrete Differential Geometry. The geometry of spheres
    Bobenko, Suris.
  • [PW08] The focal geometry of circular and conical meshes
    Pottmann, Wallner.
Discrete confocal coordinates and discrete ellipsoids
  • [BSST18] On a Discretization of Confocal Quadrics. A Geometric Approach to General Parametrizations
    Bobenko, Suris, Schief, T.
  • [HST23+] A canonical discrete analogue of the classical circular cross sections of ellipsoids and their isometric deformation
    Huang, Schief, T.
Checkerboard patterns and diagonal nets
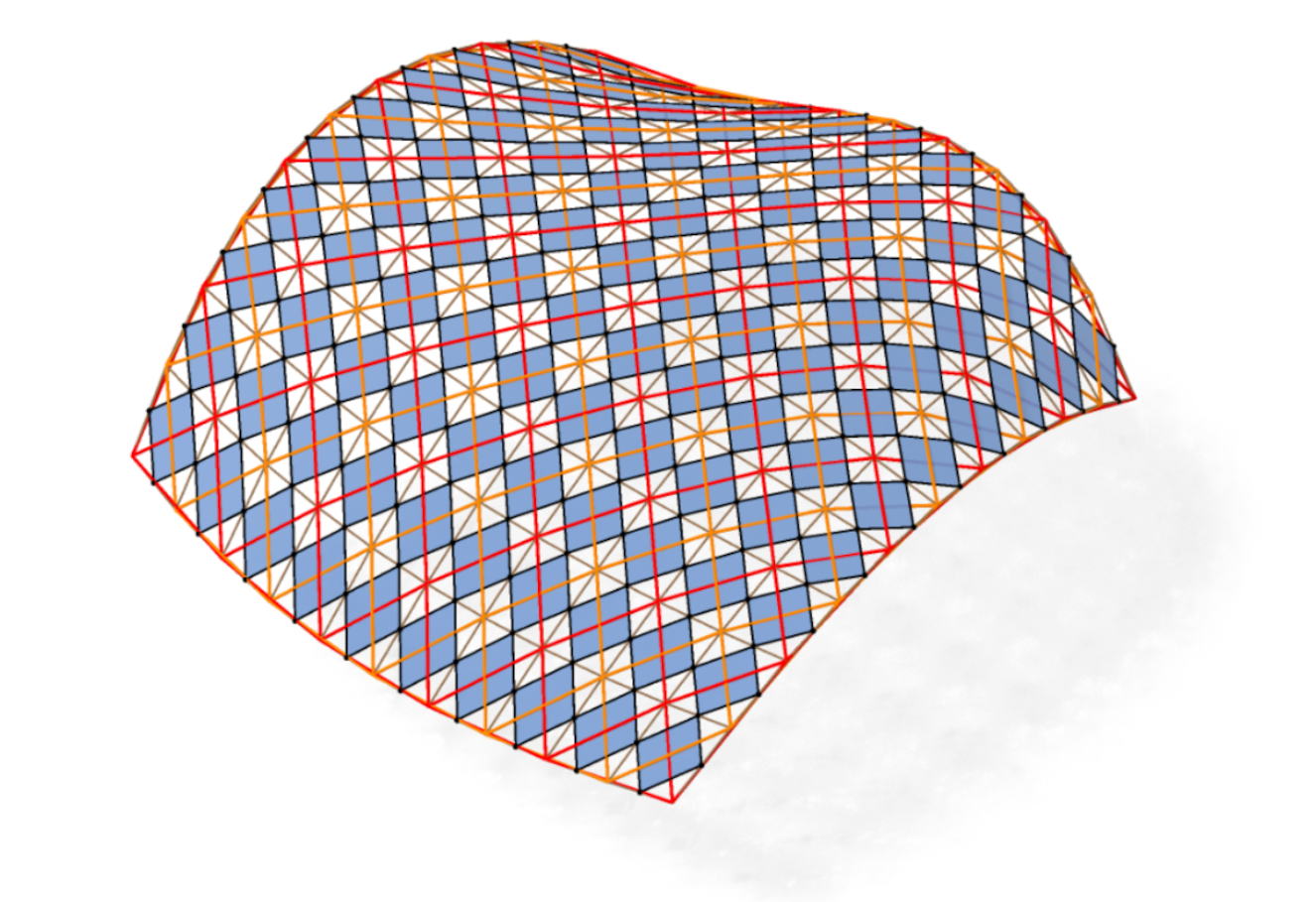
  • [PJWP19] Checkerboard patterns with black rectangles
    Peng, Jiang, Wonka, Pottmann.
  • [D22] Discrete Isothermic Nets Based on Checkerboard Patterns
    Dellinger.
Binets
A ("classical" discrete) net is a map    $\Z^2 \rightarrow \R\mathrm{P}^n$.
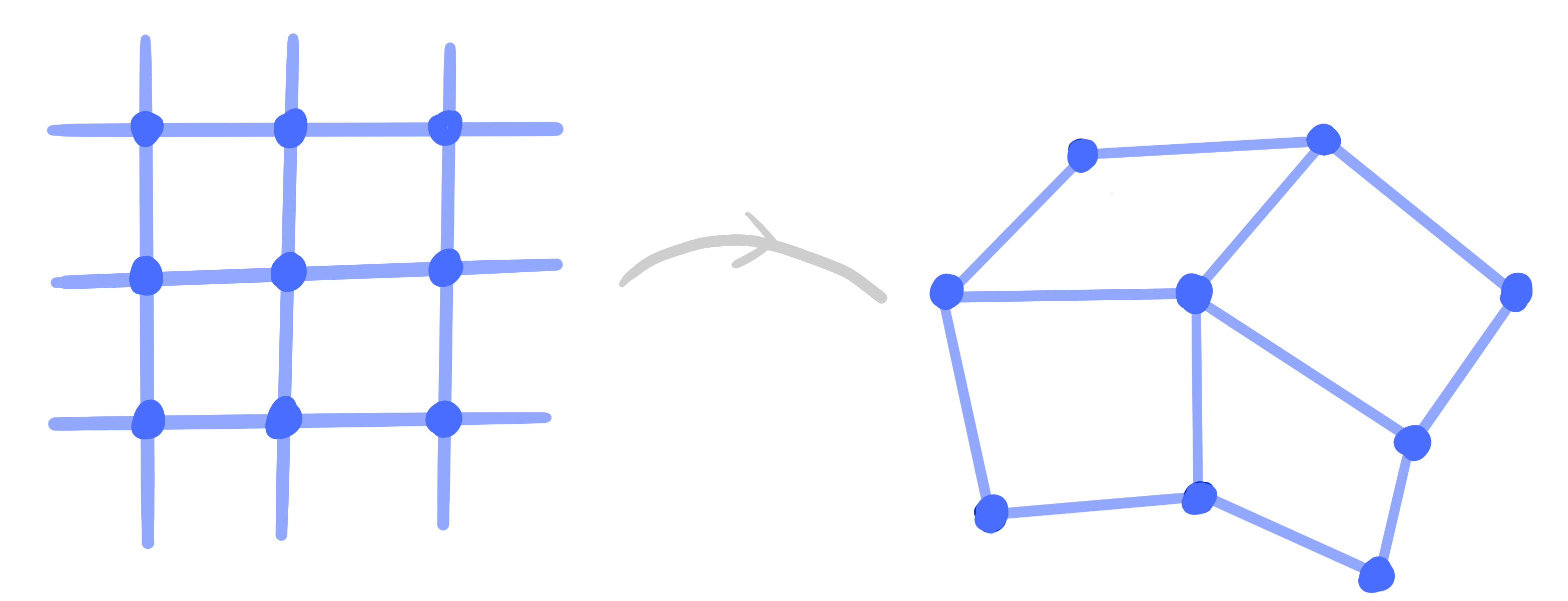
Definition:   A binet is a map    $\Z^2 \cup (\Z^2)^* \rightarrow \R\mathrm{P}^n$,    $(\Z^2)^* = F(\Z^2)$.
Some notation
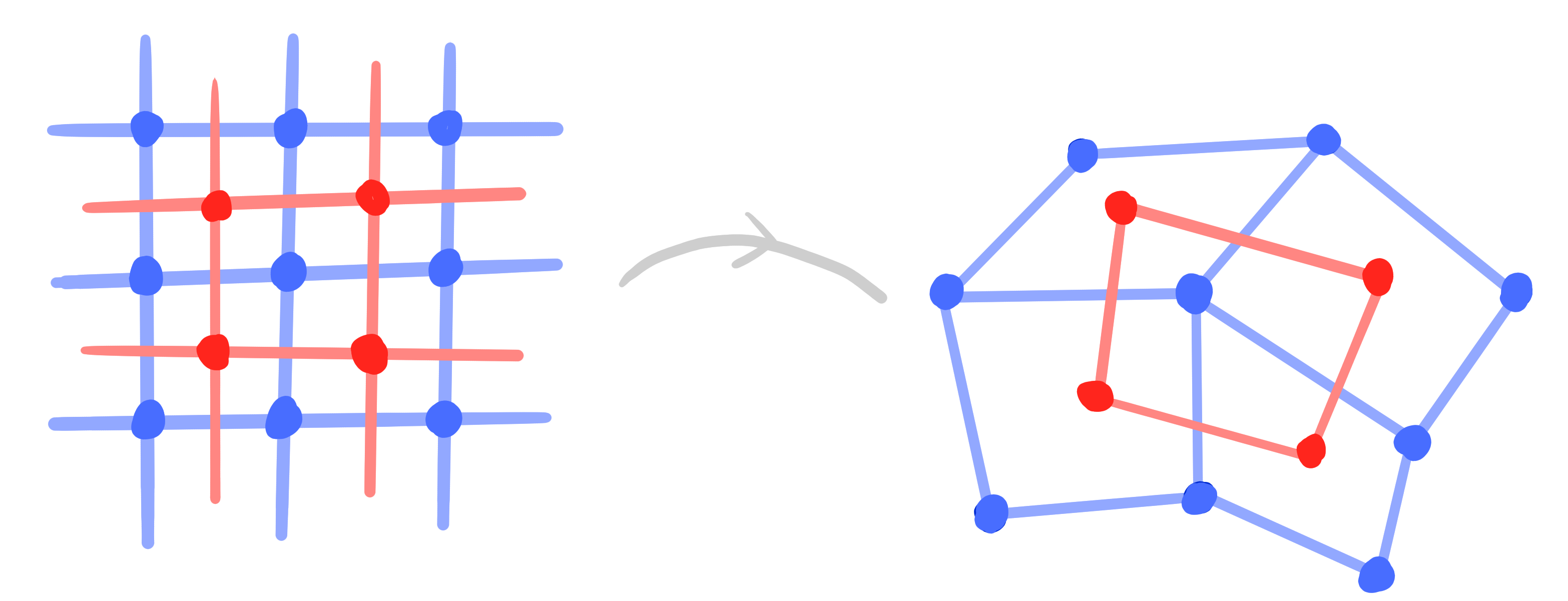
  • vertices    $V = V(\Z^2) = \Z^2$
  • edges    $E = E(\Z^2)$
  • faces    $F = F(\Z^2) = (\Z^2)^*$

  • double graph    $D = V \cup F$ ,$\qquad\qquad$ then a binet is a map    $D \rightarrow \R\mathrm{P}^n$

  • crosses    $C = \left\{ (v, f, v', f') ~|~ v,v'\in V,\quad f, f'\in F,\quad v, v' \text{ incident to } f, f' \right\}$
Orthogonal binets
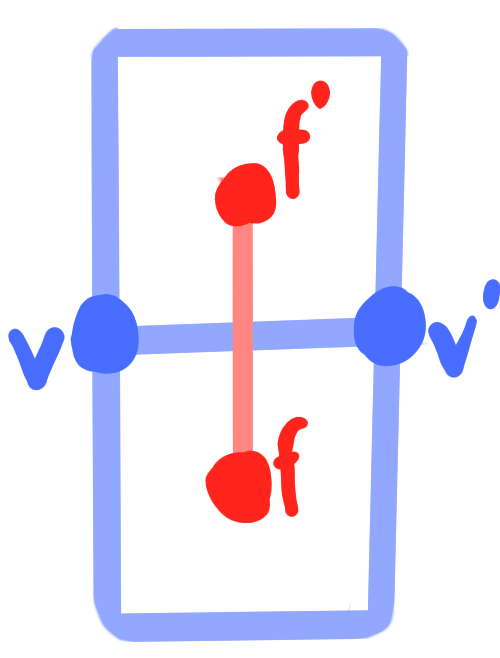
Definition:    A binet $\quad b : D \rightarrow \R^3 \quad$ is called orthogonal
$\quad \Leftrightarrow \quad b(v) \vee b(v') \perp b(f) \vee b(f') \quad$ for all crosses $\quad (v, f, v', f') \in C$

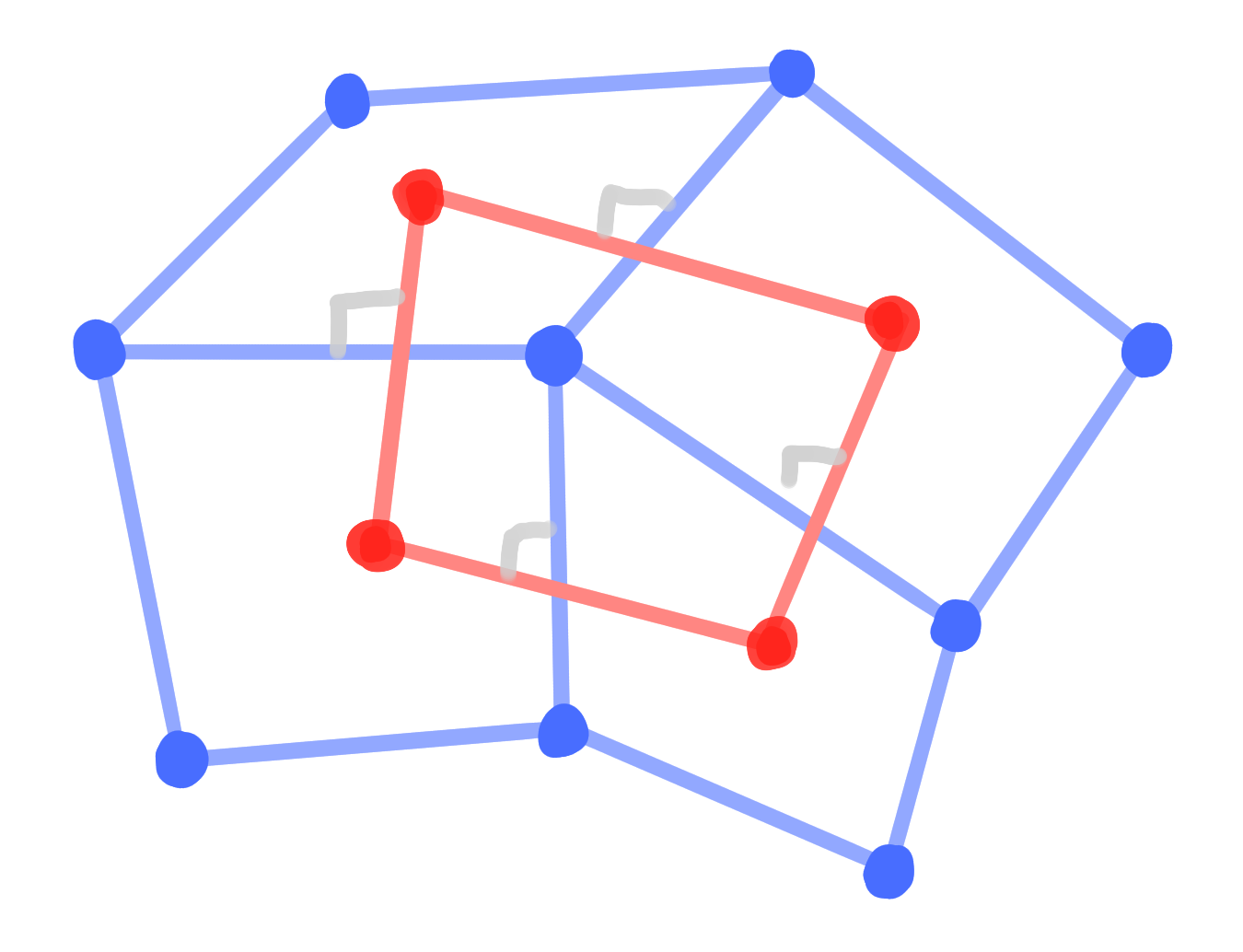
Invariances:
  • independent translation of $b|_V$ and $b|_F$
  • similarity transformations
  • a priori, not Möbius invariant
Möbius lift of orthogonal binets
Theorem:    Let $\quad b : D \rightarrow \R^3\quad$ be an orthogonal binet.
Then there exists a map $\quad S : D \rightarrow \left\{ \text{spheres in } \R^3\right\} \quad$ such that
  • for $d \in D$ the point $b(d)$ is the center of $S(d)$, and
  • for incident $v \in V$ and $f \in F$: $\quad S(v) \perp S(f)$.
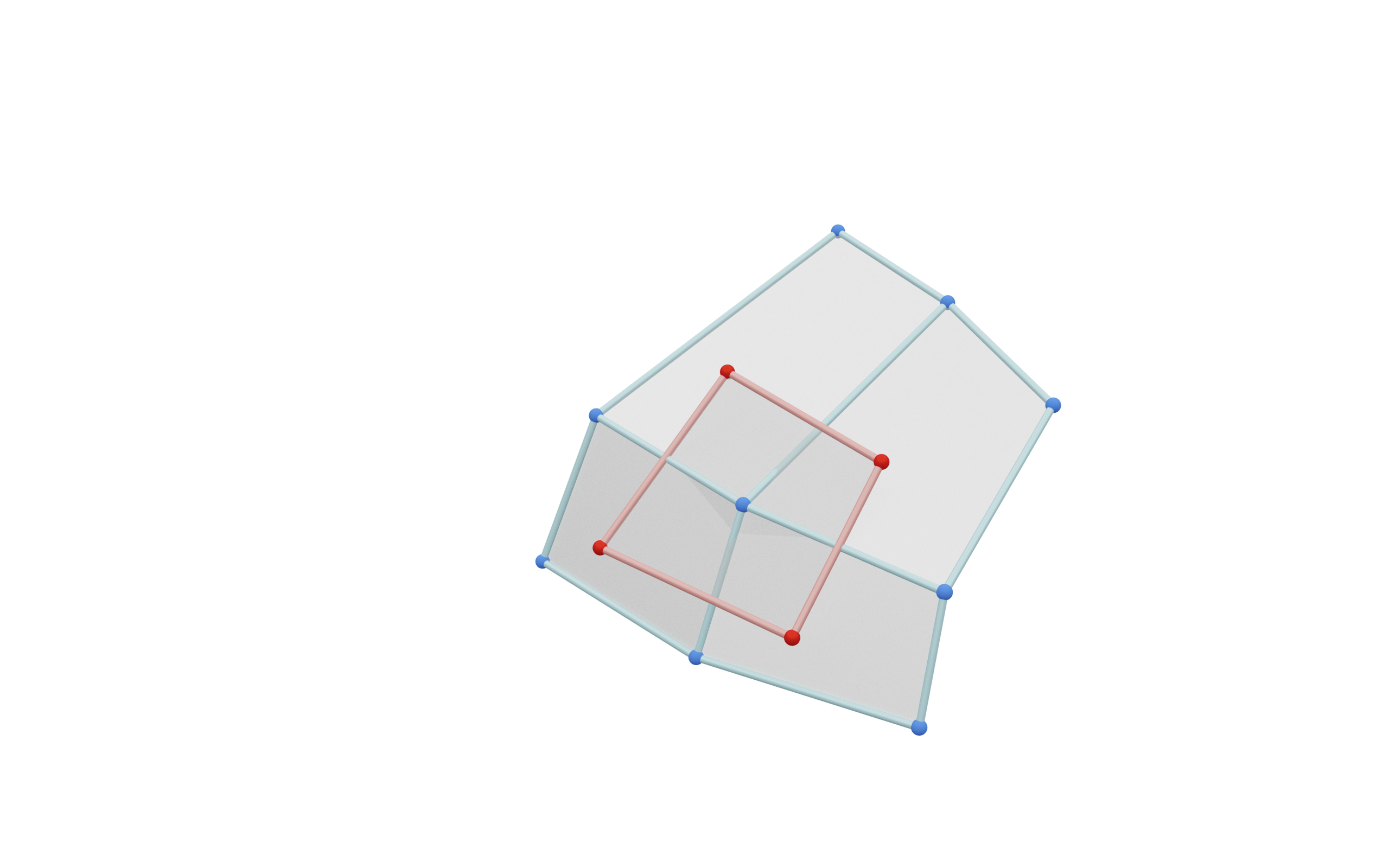
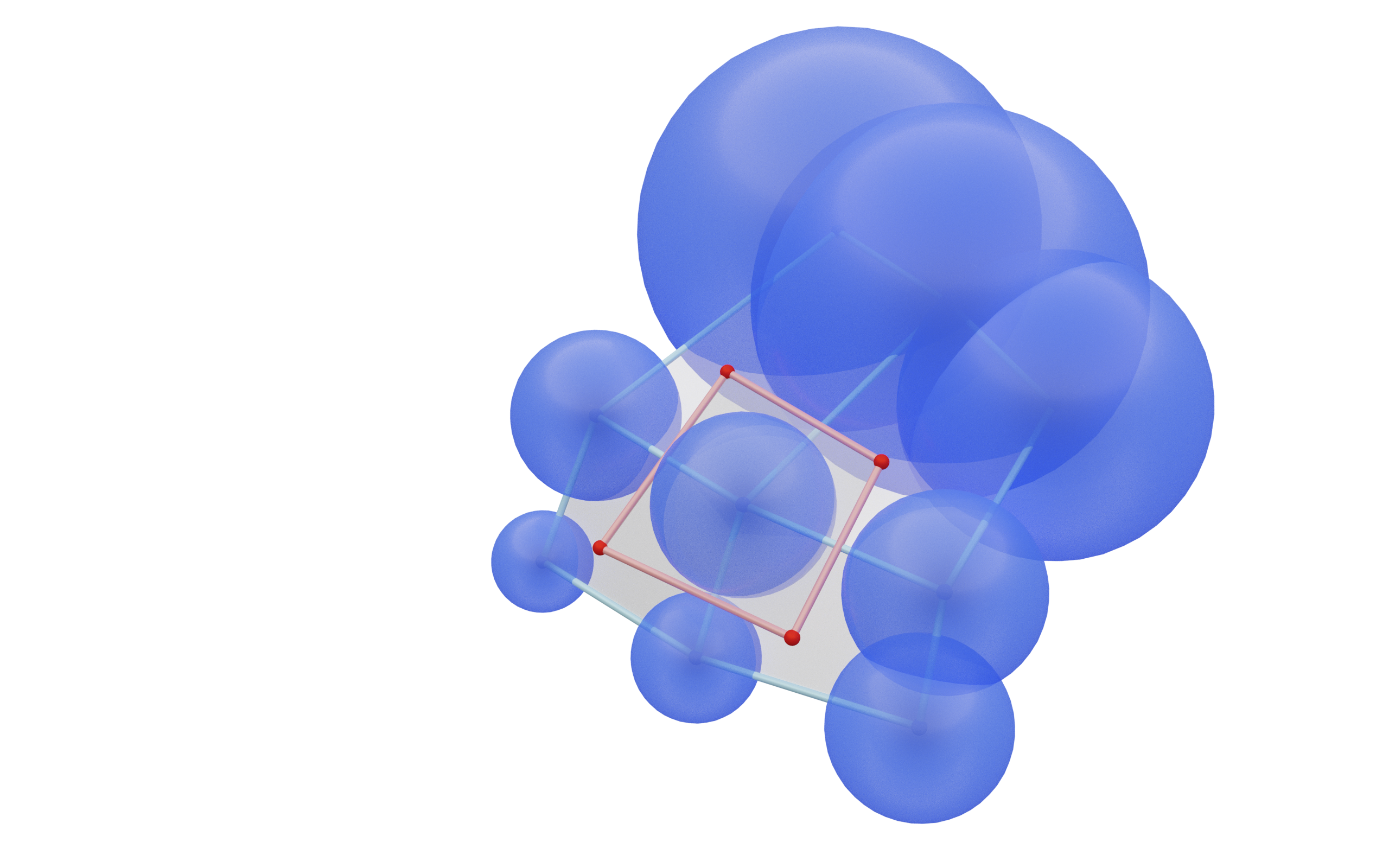
  • The construction of $S$ has 1 degree of freedom (radius of one sphere).
  • Orthogonal binets are Möbius invariant (apply Möbius transformations to the spheres).
Projective model of Möbius geometry: \[ \mathcal{M} = \left\{ \mathbf{x} = [x] \in \R\mathrm{P}^4 ~|~ \langle x, x \rangle_{\mathcal{M}} = x_1^2 + x_2^2 + x_3^2 + x_4^2 - x_5^2 = 0 \right\} \subset \R\mathrm{P}^4\\ \]
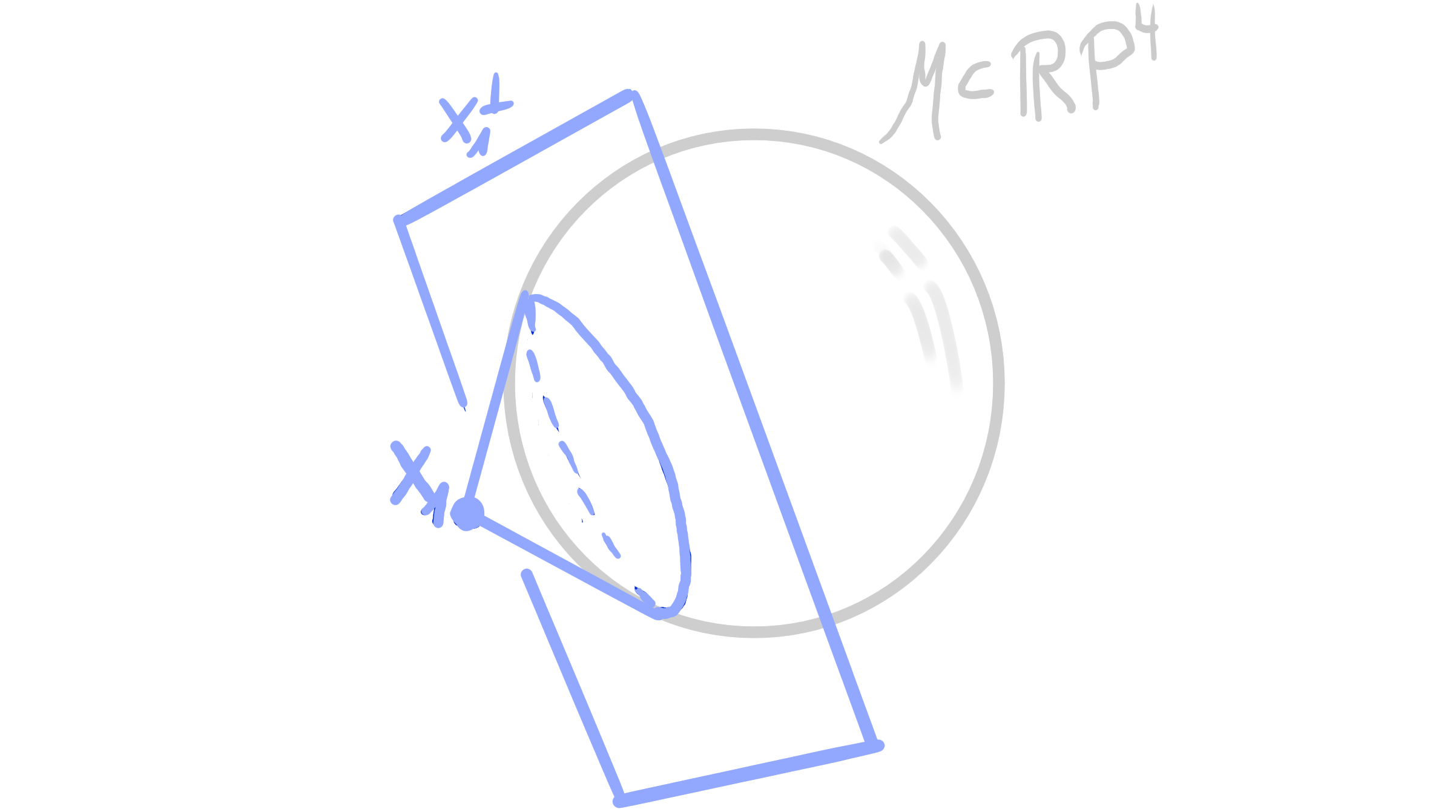
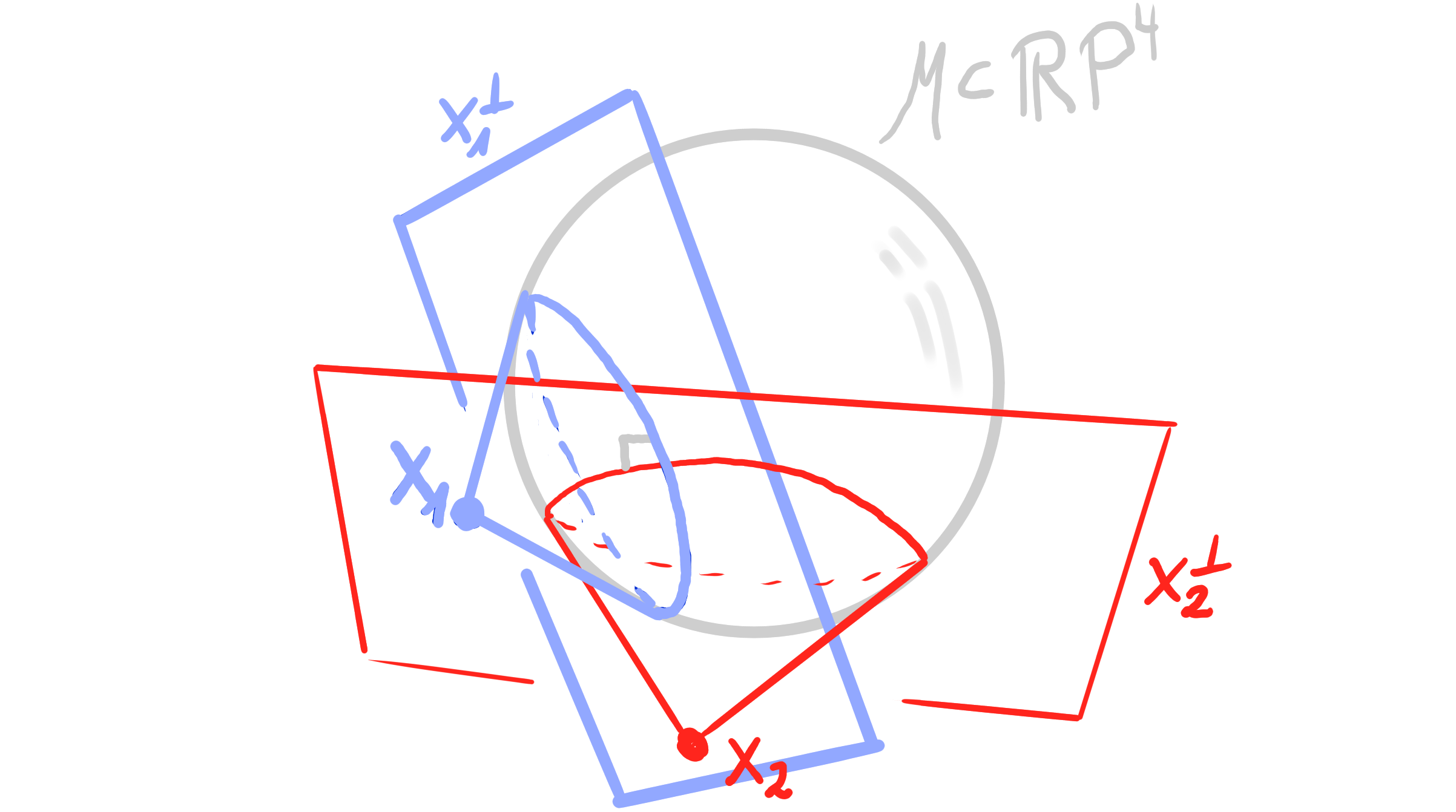
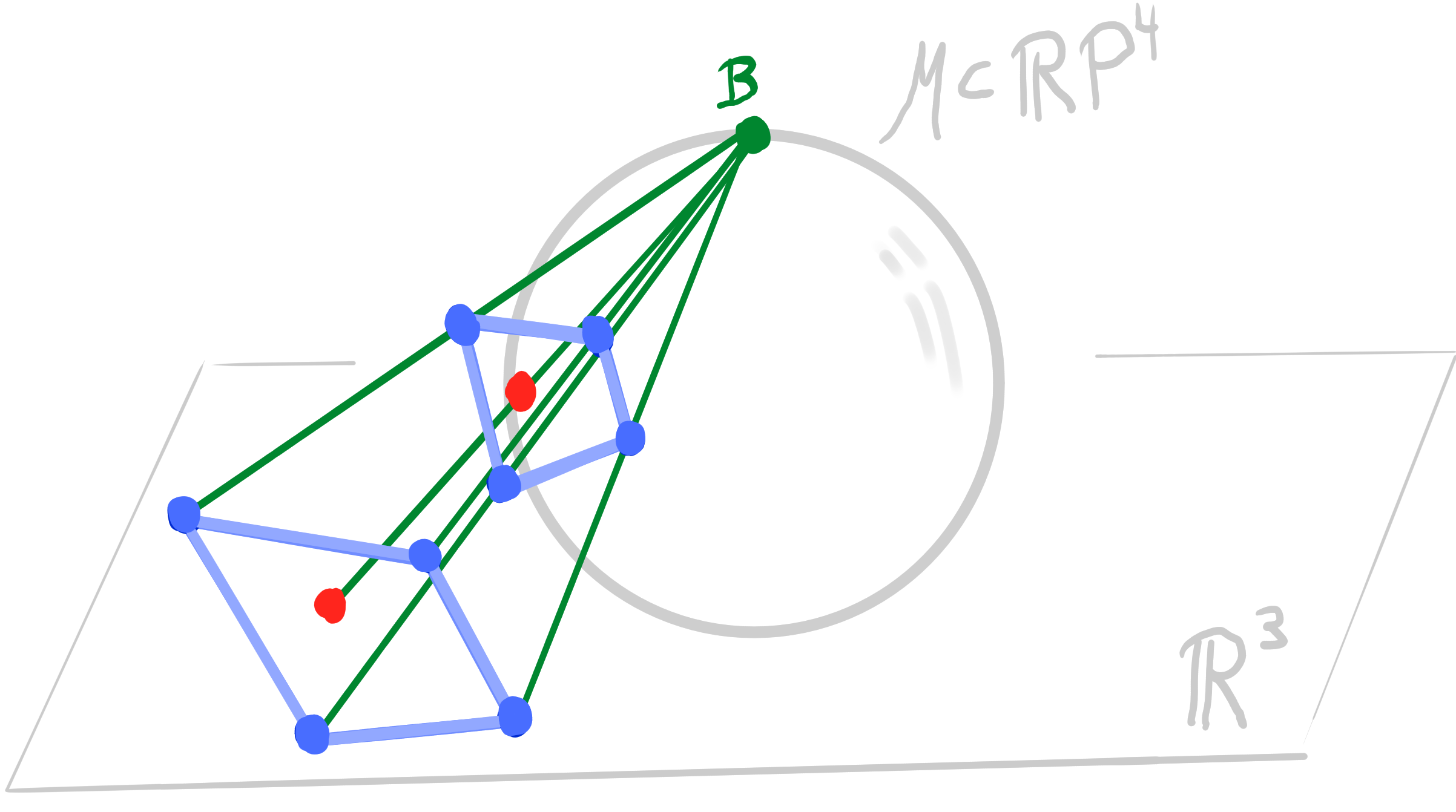
  • a sphere $S \subset \mathcal{M}$ is represented by a point $\mathbf{x} \in \R\mathrm{P}^4$ via polarity: $\qquad S = \mathbf{x}^\perp \cap \mathcal{M}$
  • $ S_1 \perp S_2 \quad \Leftrightarrow \quad \mathbf{x}_1 \perp \mathbf{x}_2 \quad \Leftrightarrow \quad \langle x_1, x_2 \rangle_{\mathcal{M}} = 0 $
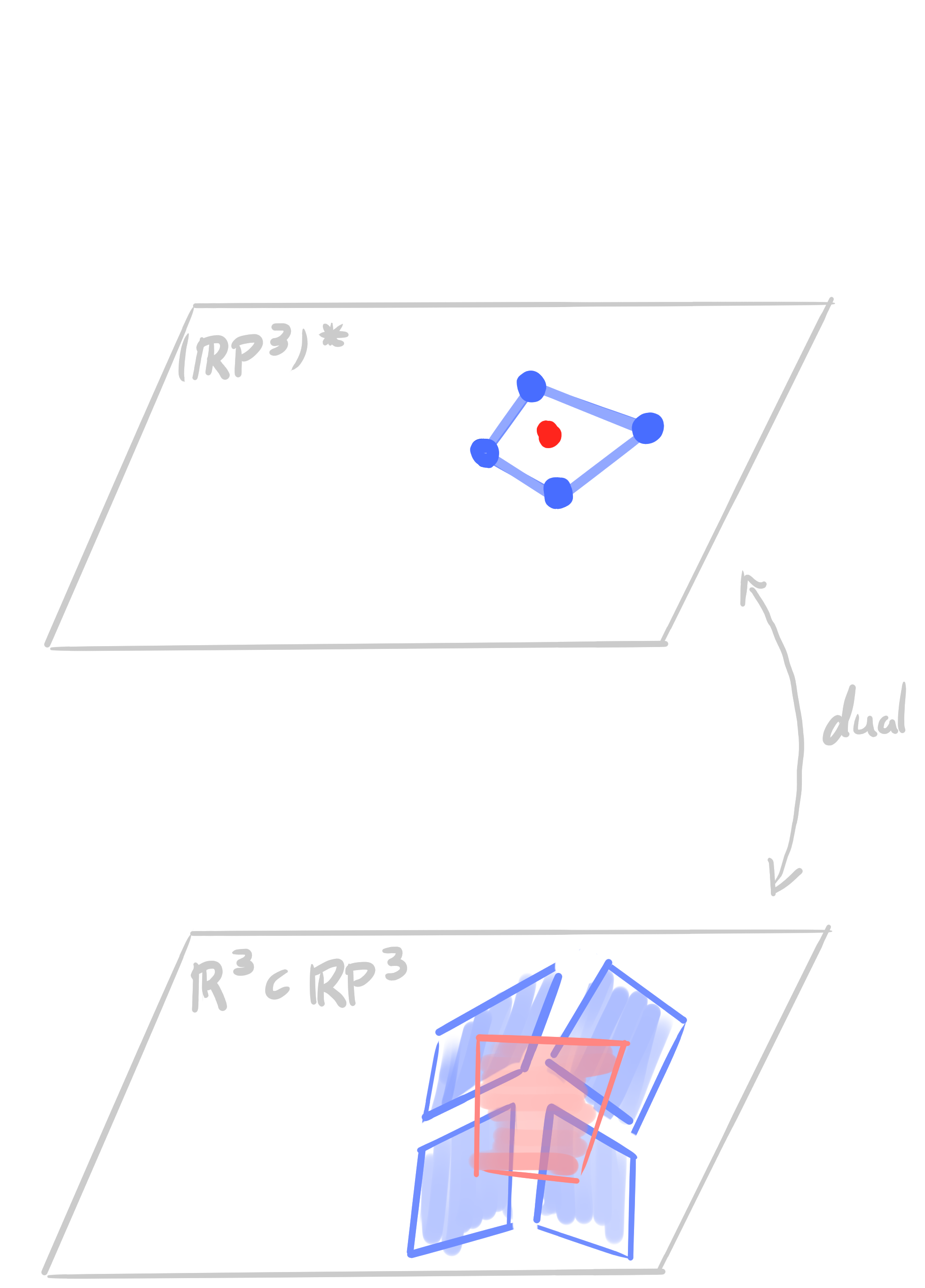
Theorem:
Let $~ b : D \rightarrow \R^3\,$ be an orthogonal binet. Then there exists a lift $~b_{\mathcal{M}} : D \rightarrow \R P^4$ such that \[ \begin{aligned} &\pi_{\mathbf{B}} \circ b_{\mathcal{M}}= b\\ &b_{\mathcal{M}}(v) \perp b_{\mathcal{M}}(f) \end{aligned} \]

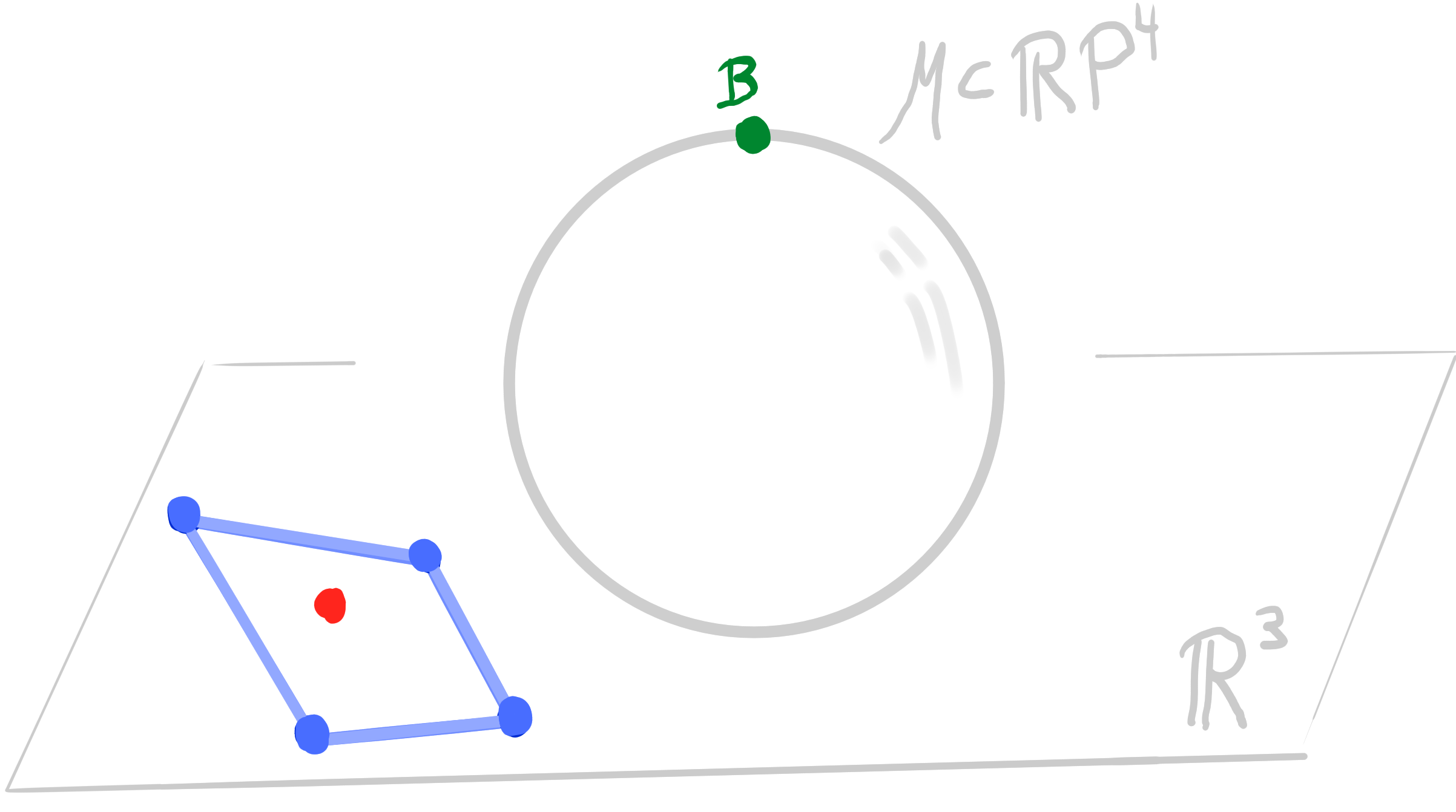
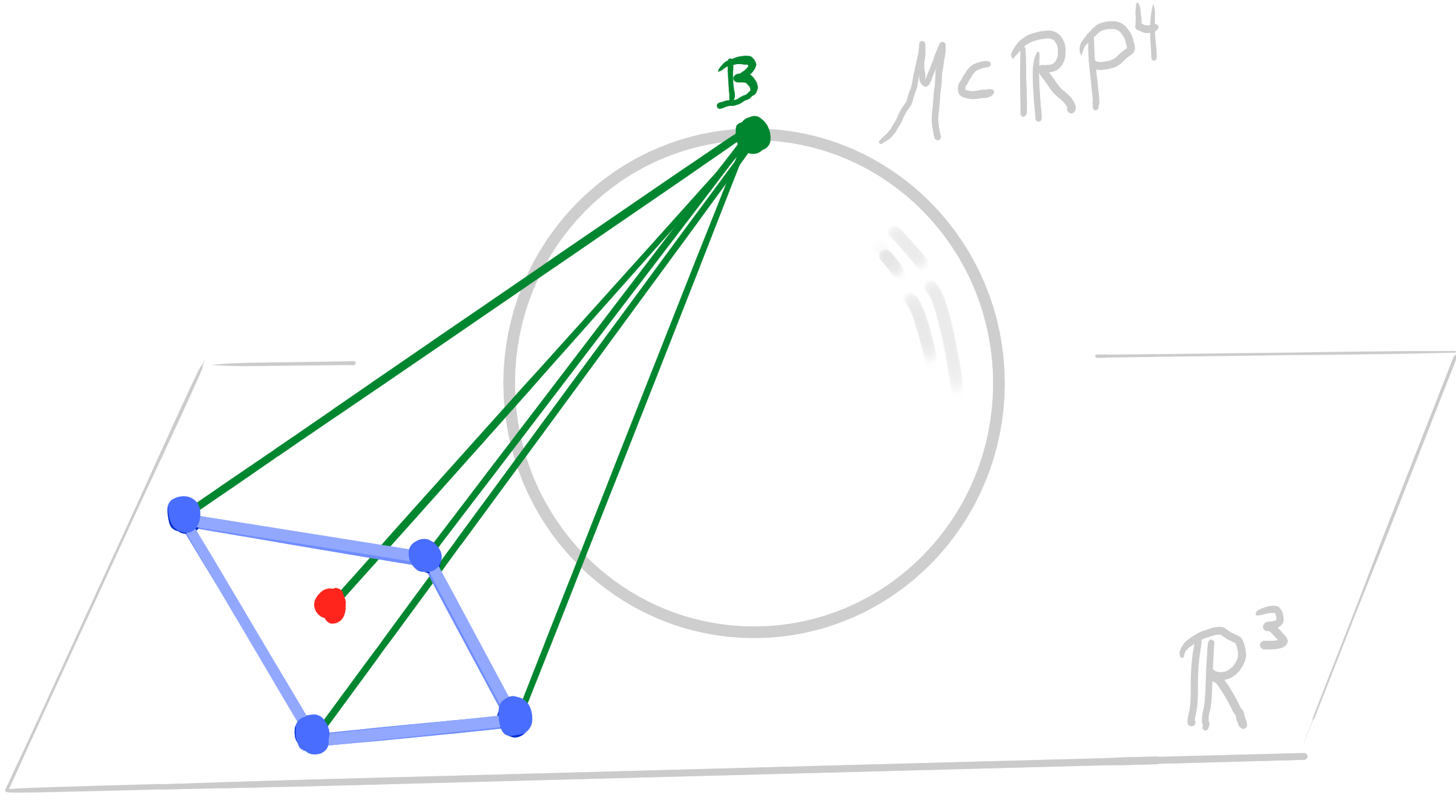
  • Orthogonality in $\R^3$ becomes polarity in $\R\mathrm{P}^4$ in the lift.
  • The Möbius lift has 1 degree of freedom (radius of one sphere).
  • Points of the lift can lie inside $\mathcal{M}$ (spheres with imaginary radius).
Definition:
Let $\mathcal{Q} \subset \R\mathrm{P}^n$ be a quadric.
A polar binet is a map $~ b : D \rightarrow \R\mathrm{P}^n ~$ such that
for any two incident $v \in V$ and $f \in F$ the two points $b(v)$ and $b(f)$ are polar: \[ b(v) \perp b(f) \]
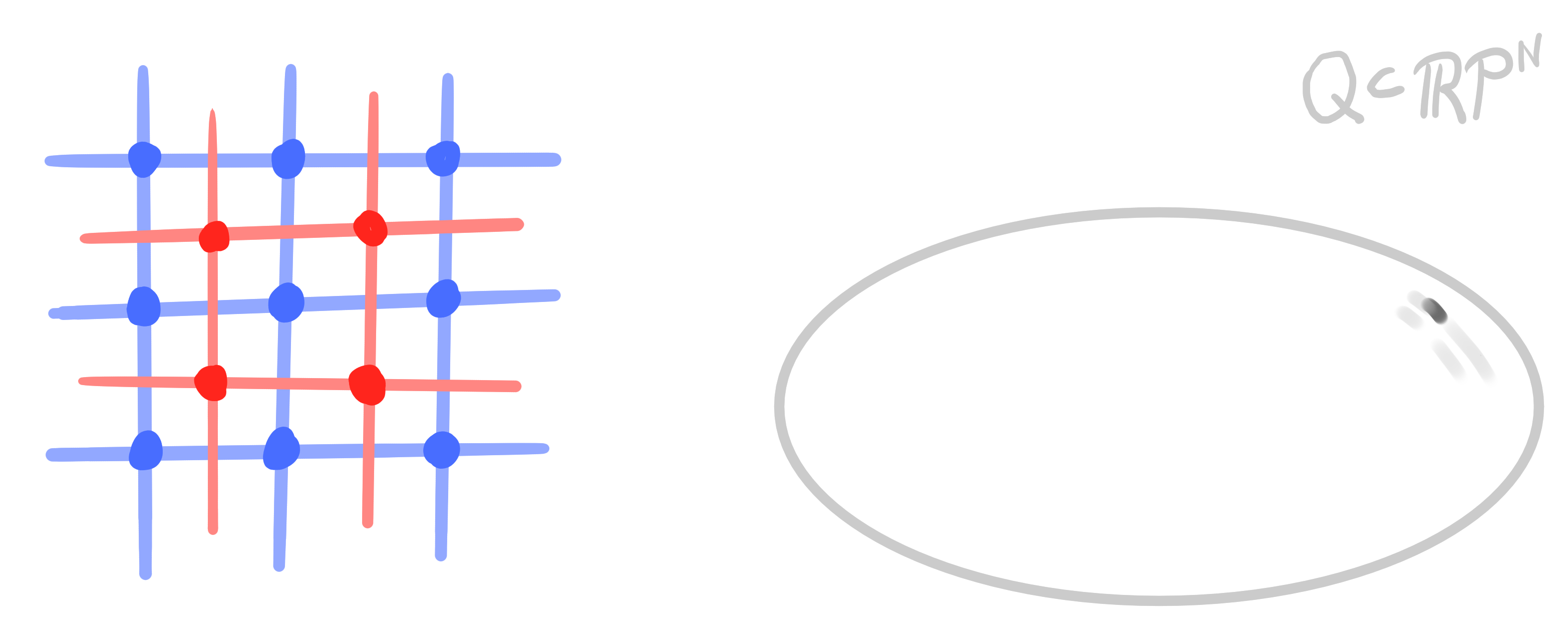
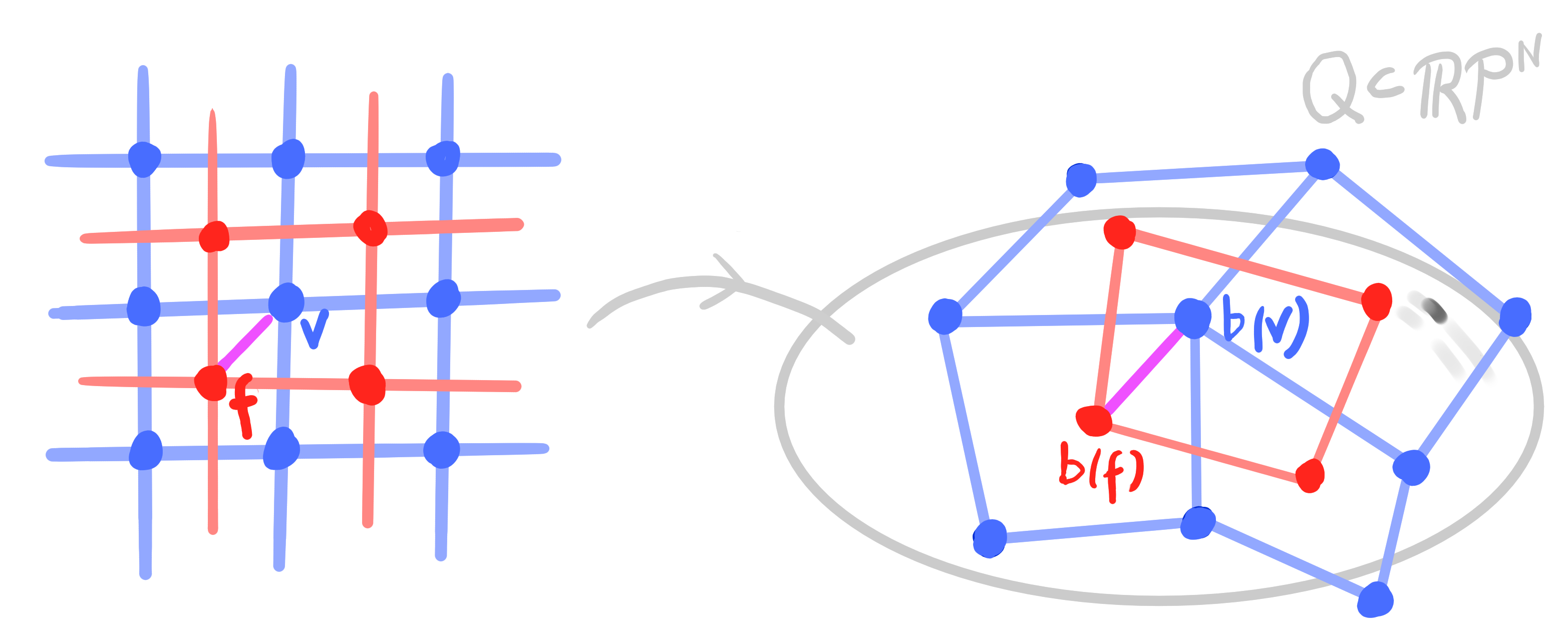
Conclusion:
Orthogonal binets in $\R^3$ can be lifted to polar binets in $\R\mathrm{P}^4$.
Vice versa, polar binets in $\R\mathrm{P}^4$ project to orthogonal binets in $\R^3$.
Bi*nets
A *net is a map $~V \rightarrow \mathrm{Planes}(\R\mathrm{P}^n)~$ such that adjacent planes intersect in a line.
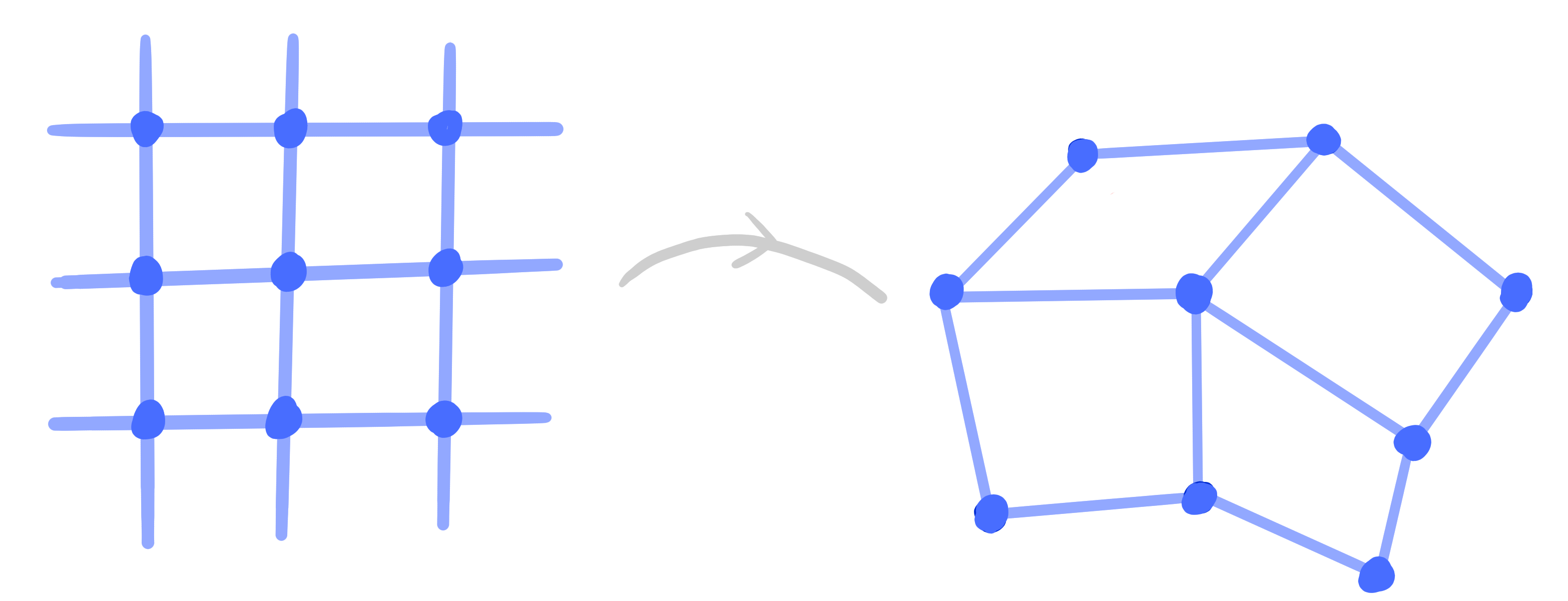
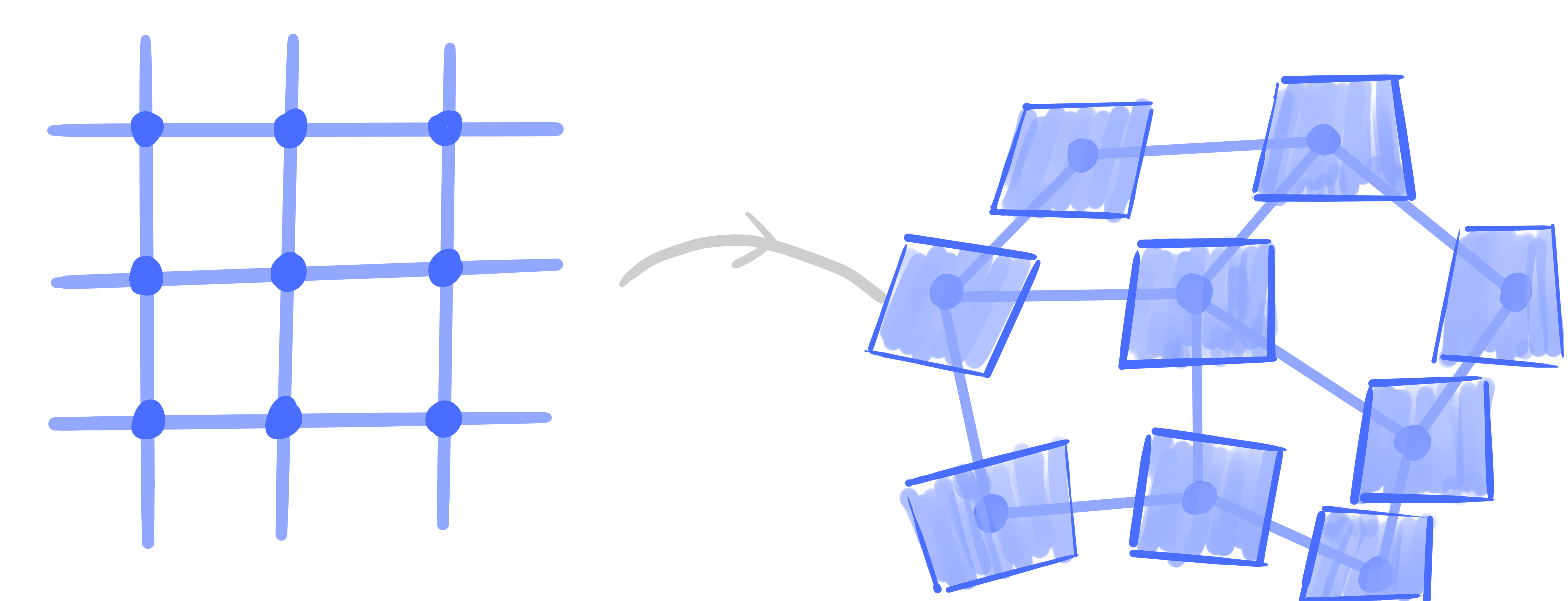
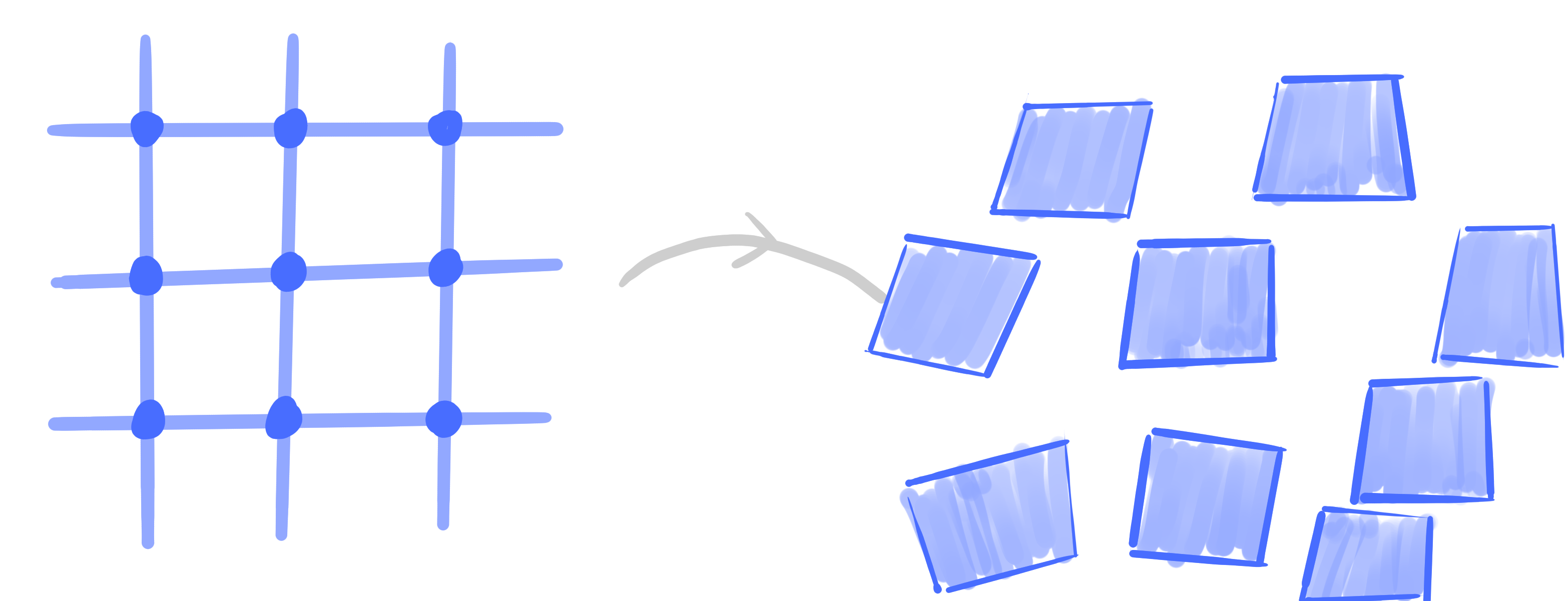
Definition
A bi*net is a map $~D \rightarrow \mathrm{Planes}(\R\mathrm{P}^n)~$ such that $b|_V$ and $b|_F$ are *nets.
Orthogonal bi*nets
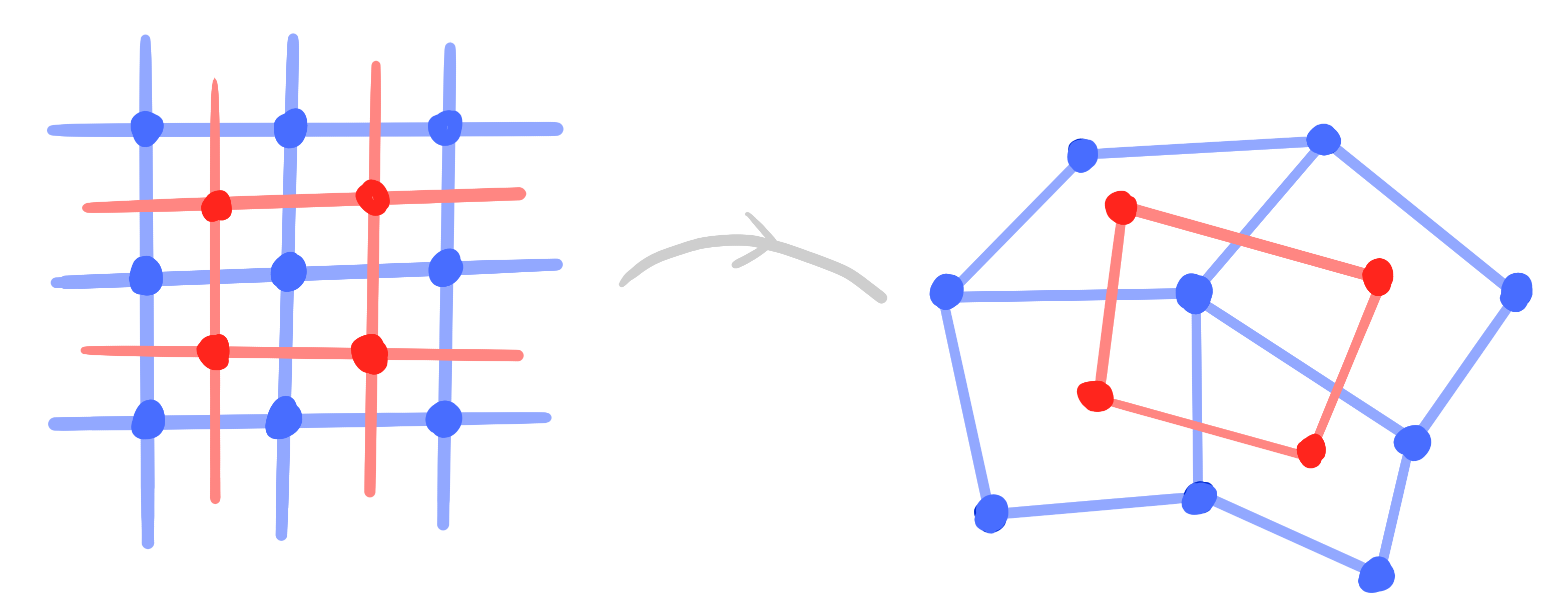
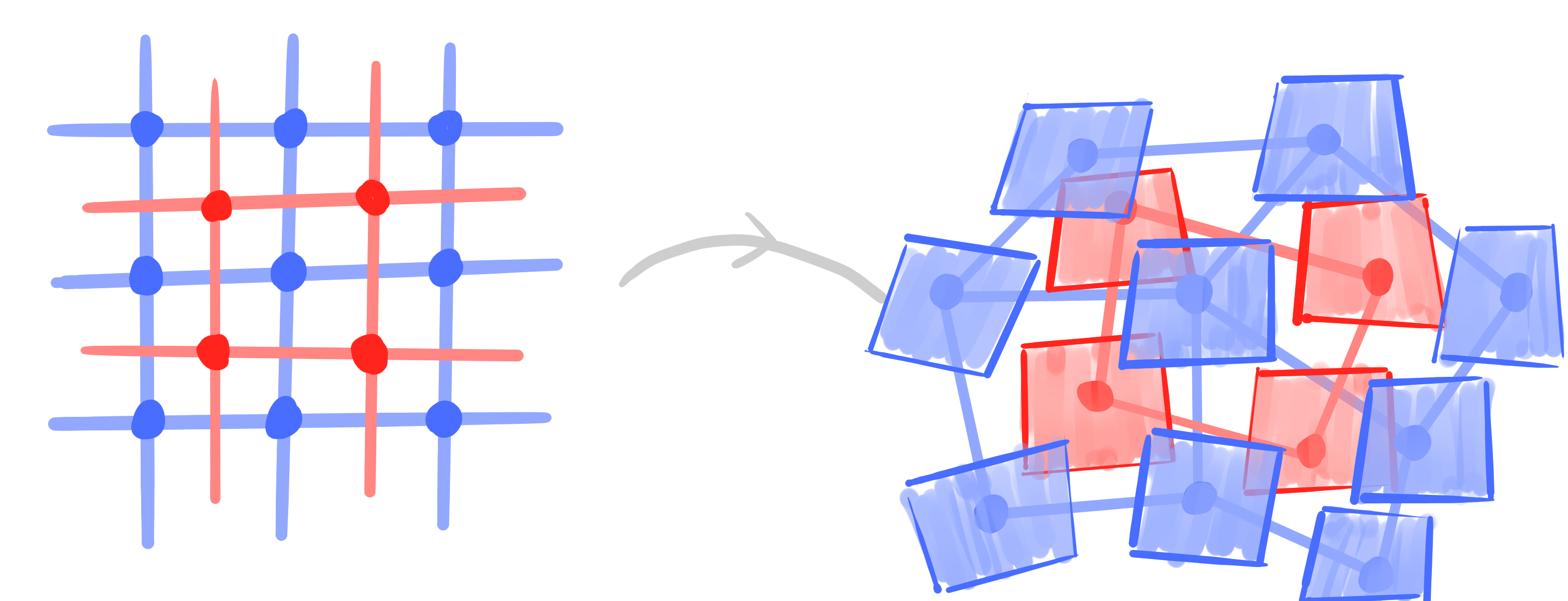
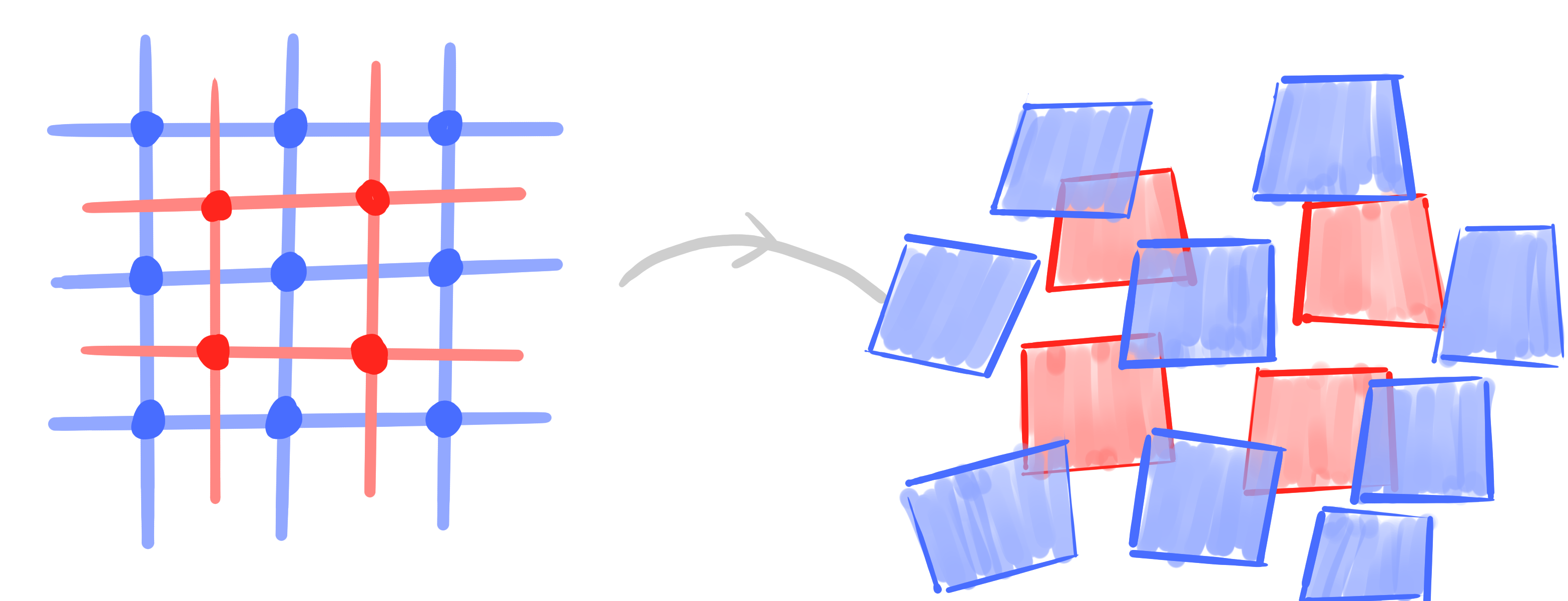
Definition:    A bi*net $\quad b : D \rightarrow \mathrm{Planes}(\R^3) \quad$ is called orthogonal
$\quad \Leftrightarrow \quad b(v) \cap b(v') \perp b(f) \cap b(f') \quad$ for all crosses $\quad (v, f, v', f') \in C$

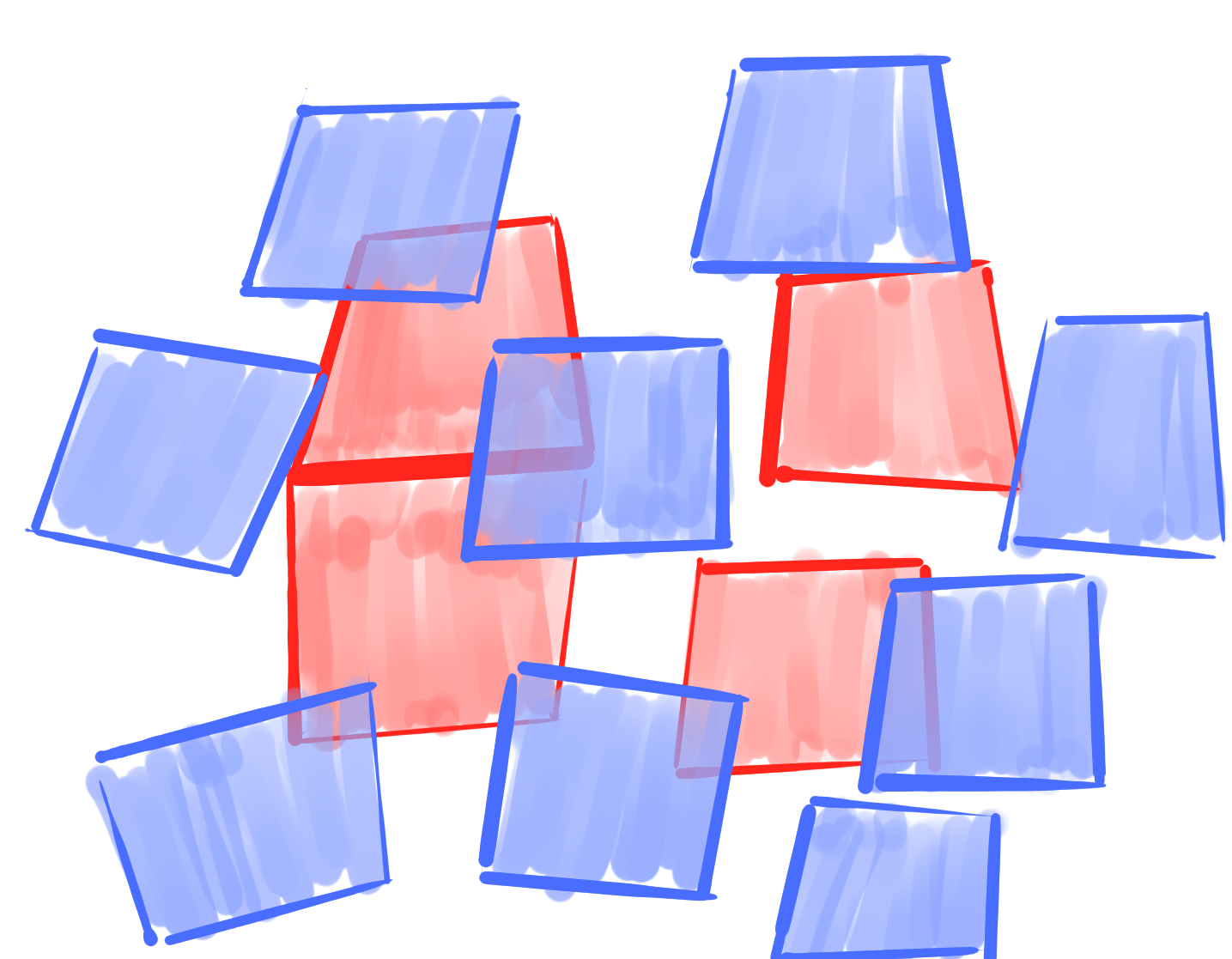
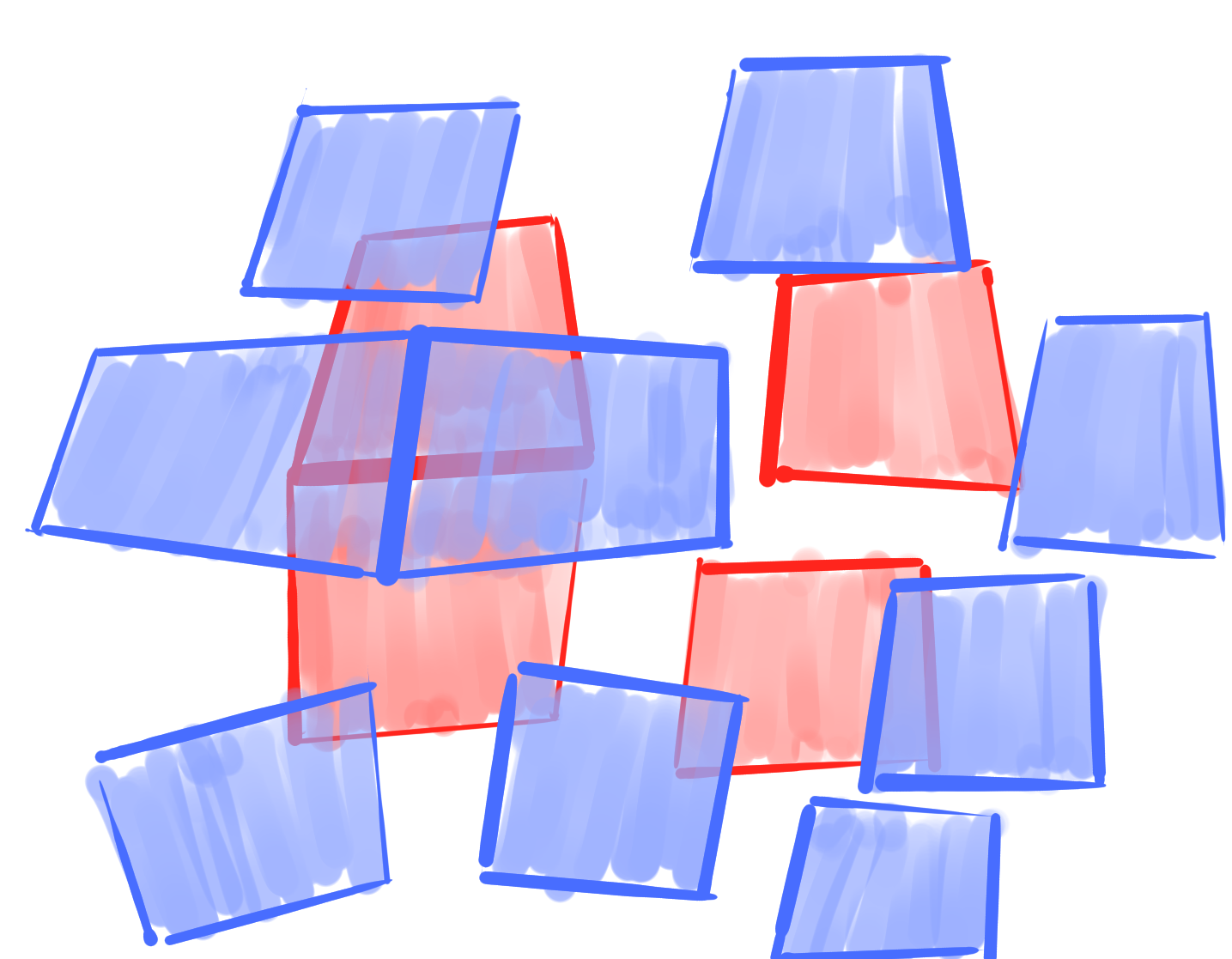
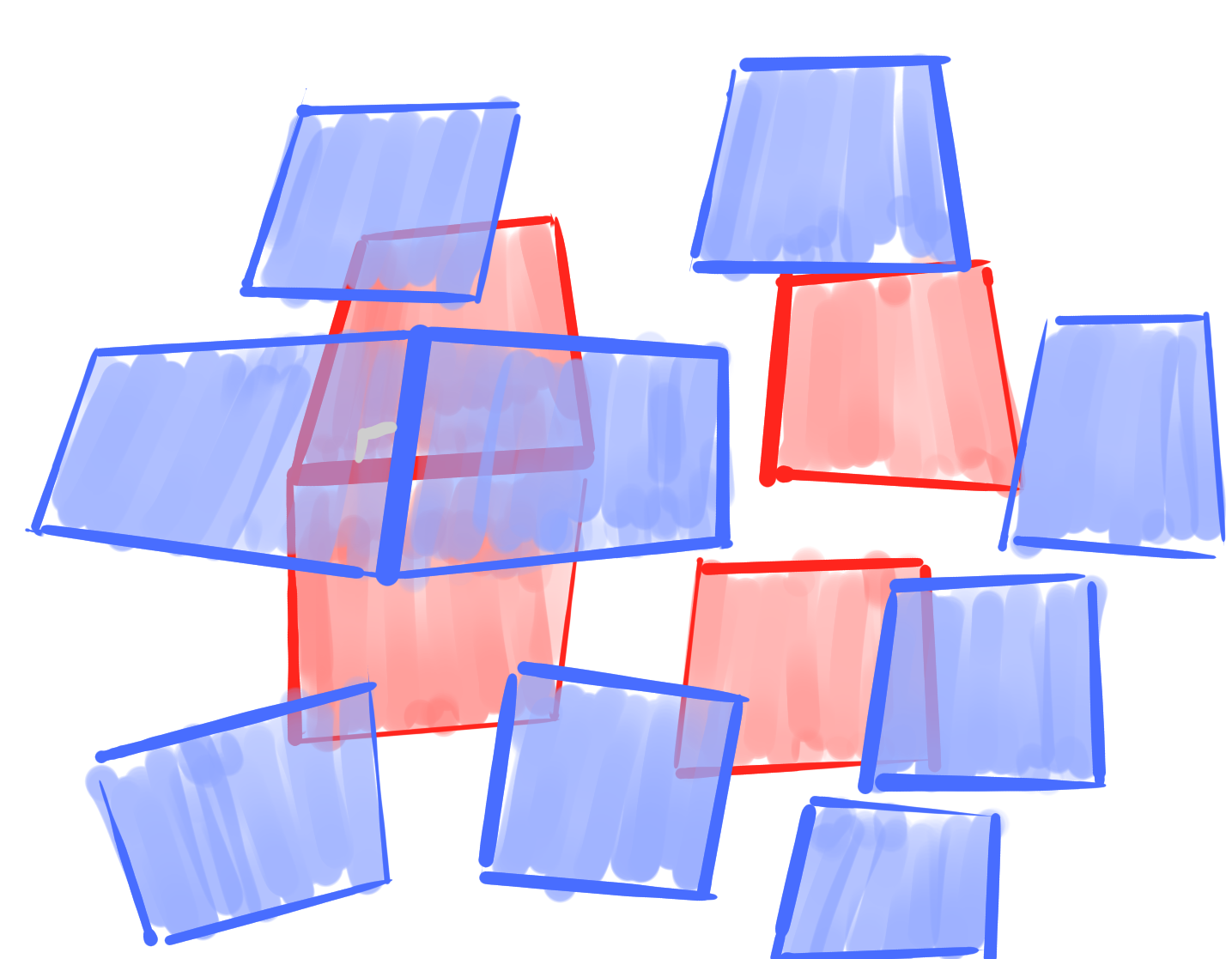
Invariances:
  • independent translation of $b|_V$ and $b|_F$
  • similarity transformations
  • a priori, not Laguerre invariant
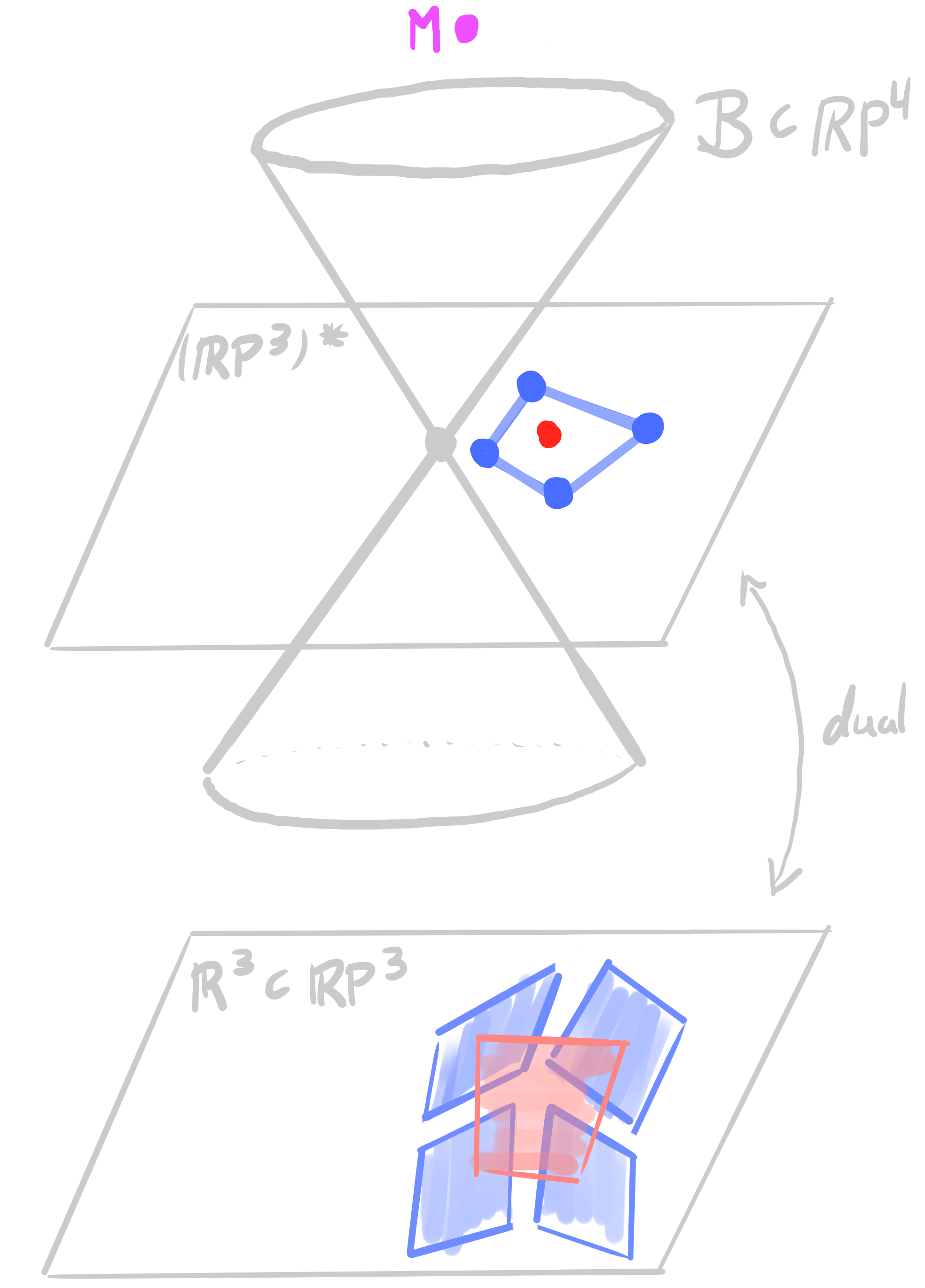
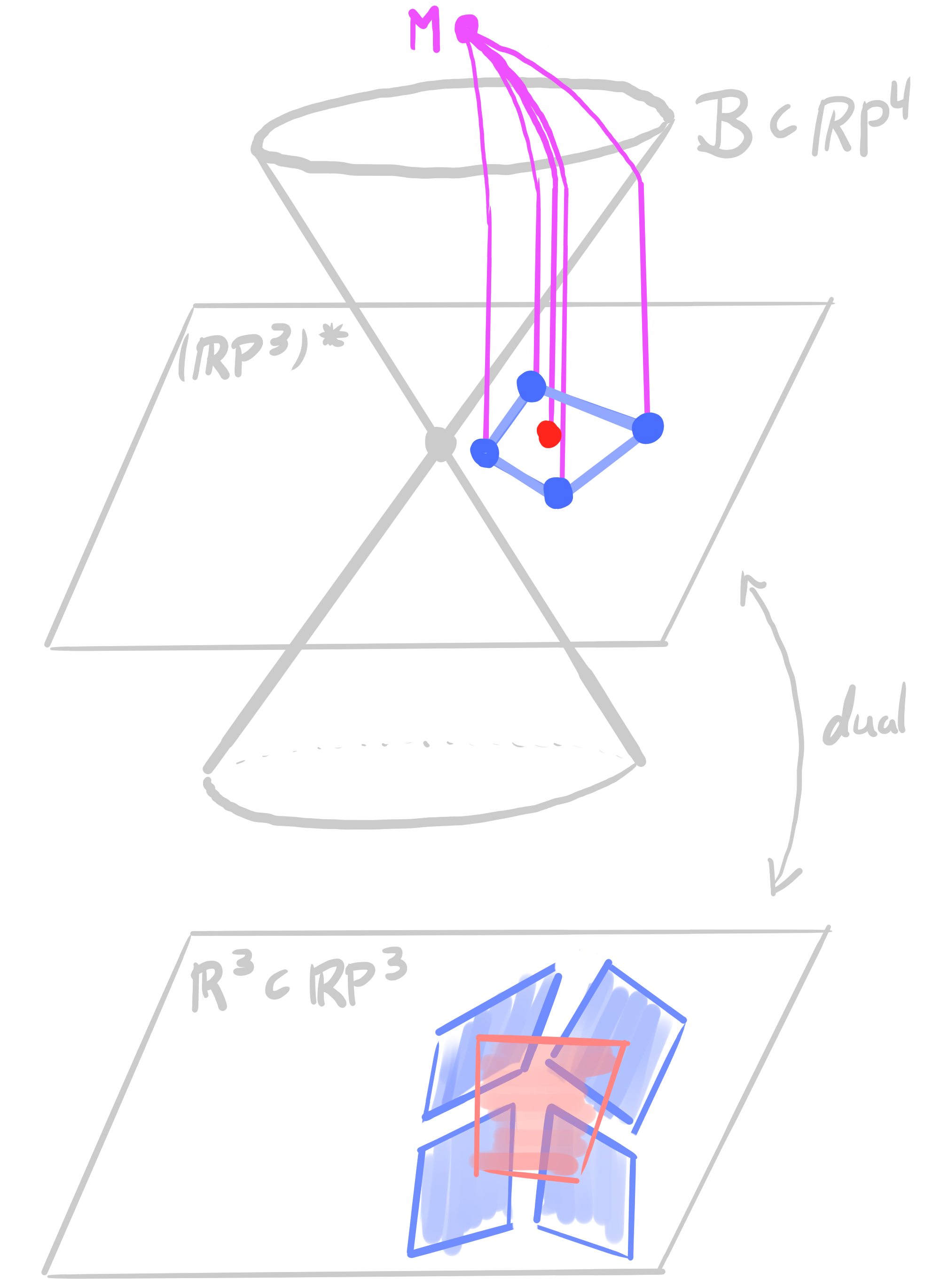
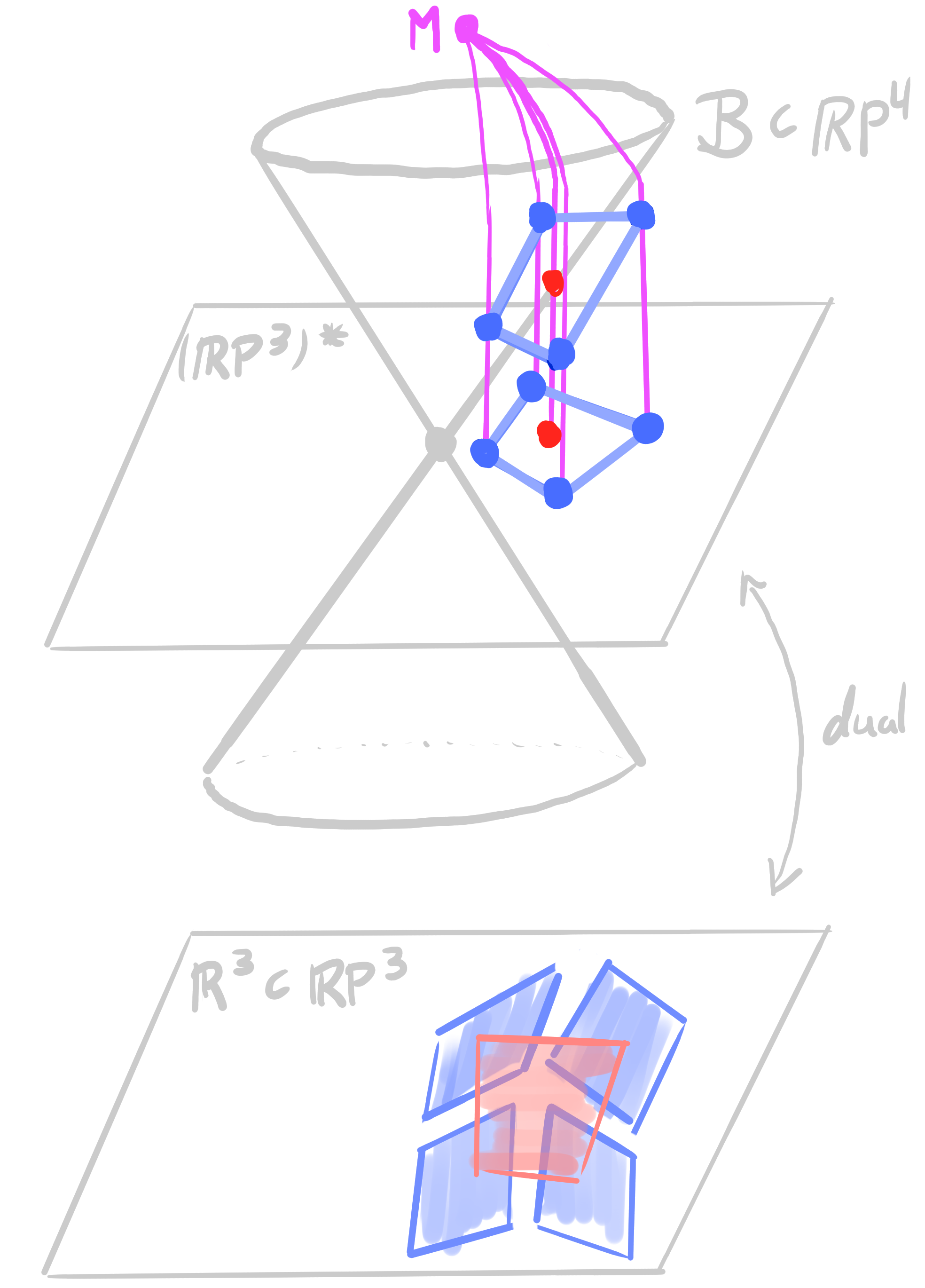
Laguerre lift of orthogonal bi*nets
Theorem:
Let $~b : D \rightarrow \mathrm{Planes}(\R^3)$ be an orthogonal bi*net. Then there exists a lift $~b_{\mathcal{B}} : D \rightarrow \R\mathrm{P}^4$ such that \[ \begin{aligned} &\pi_{\mathbf{M}} \circ b_{\mathcal{B}}= b\\ &b_{\mathcal{B}}(v) \perp b_{\mathcal{B}}(f) \end{aligned} \]
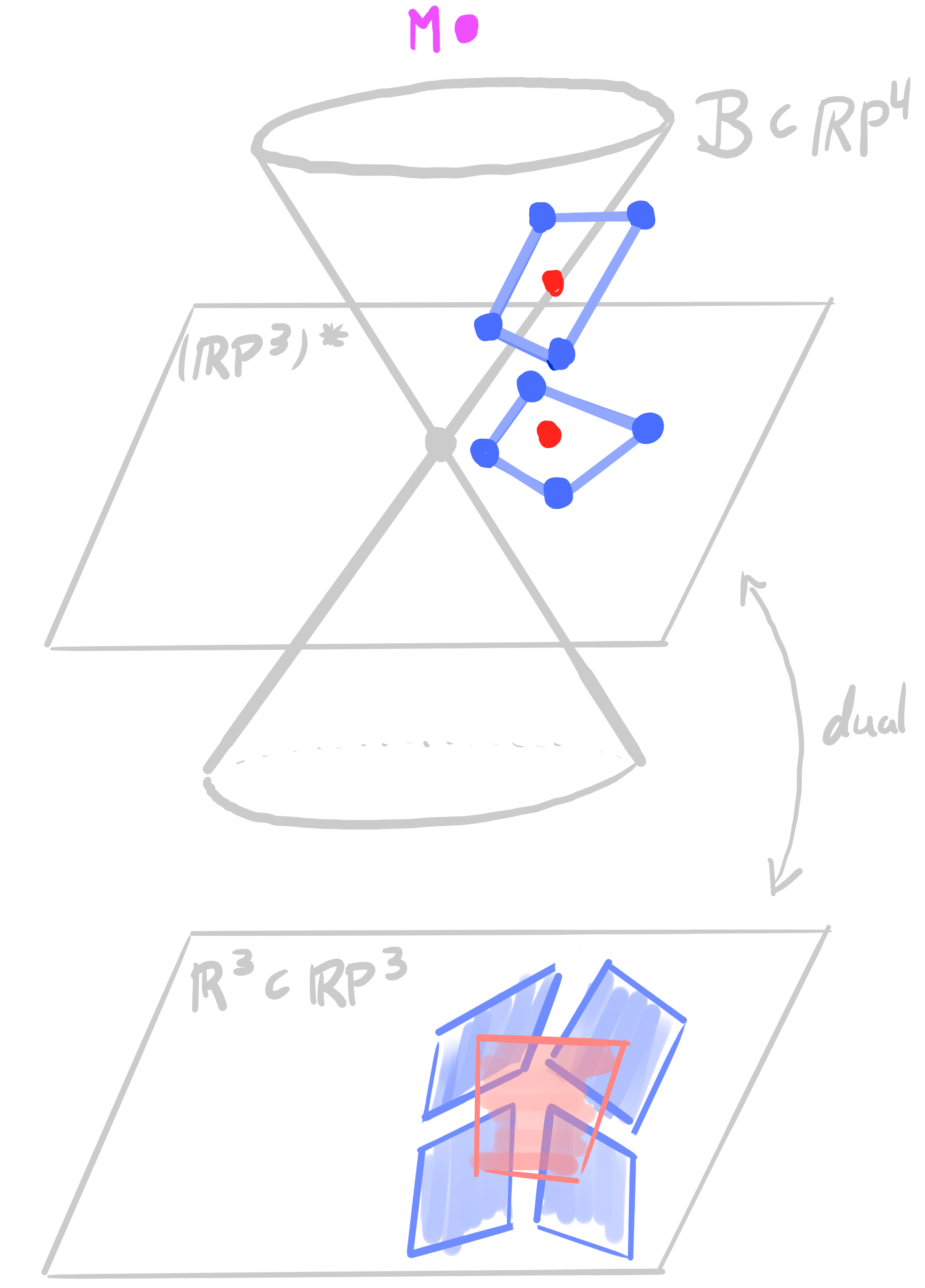
Conclusion:
Orthogonal bi*nets in $\R^3$ can be lifted to polar binets in $\R\mathrm{P}^4$.
Vice versa, polar binets in $\R\mathrm{P}^4$ project to orthogonal bi*nets in $\R^3$.
What are points not on $\mathcal{B}$, and what does polarity mean geometrically?
  • a point outside $\mathcal{B}$ represents a plane with an angle
  • $\mathbf{x}_1 \perp \mathbf{x}_2 \quad \Leftrightarrow \quad \pi_{\mathbf{B}(\mathbf{x}_1)} \perp \pi_{\mathbf{B}(\mathbf{x}_2)} \quad$ polar Gauss map
  • orthogonal circles on $\mathbb{S}^2$
Conjugate binets
Definition:
A binet $~ b : D \rightarrow \R^3 ~$ is called conjugate
$\Leftrightarrow$ $b|_V$ and $b|_F$ are Q-nets.


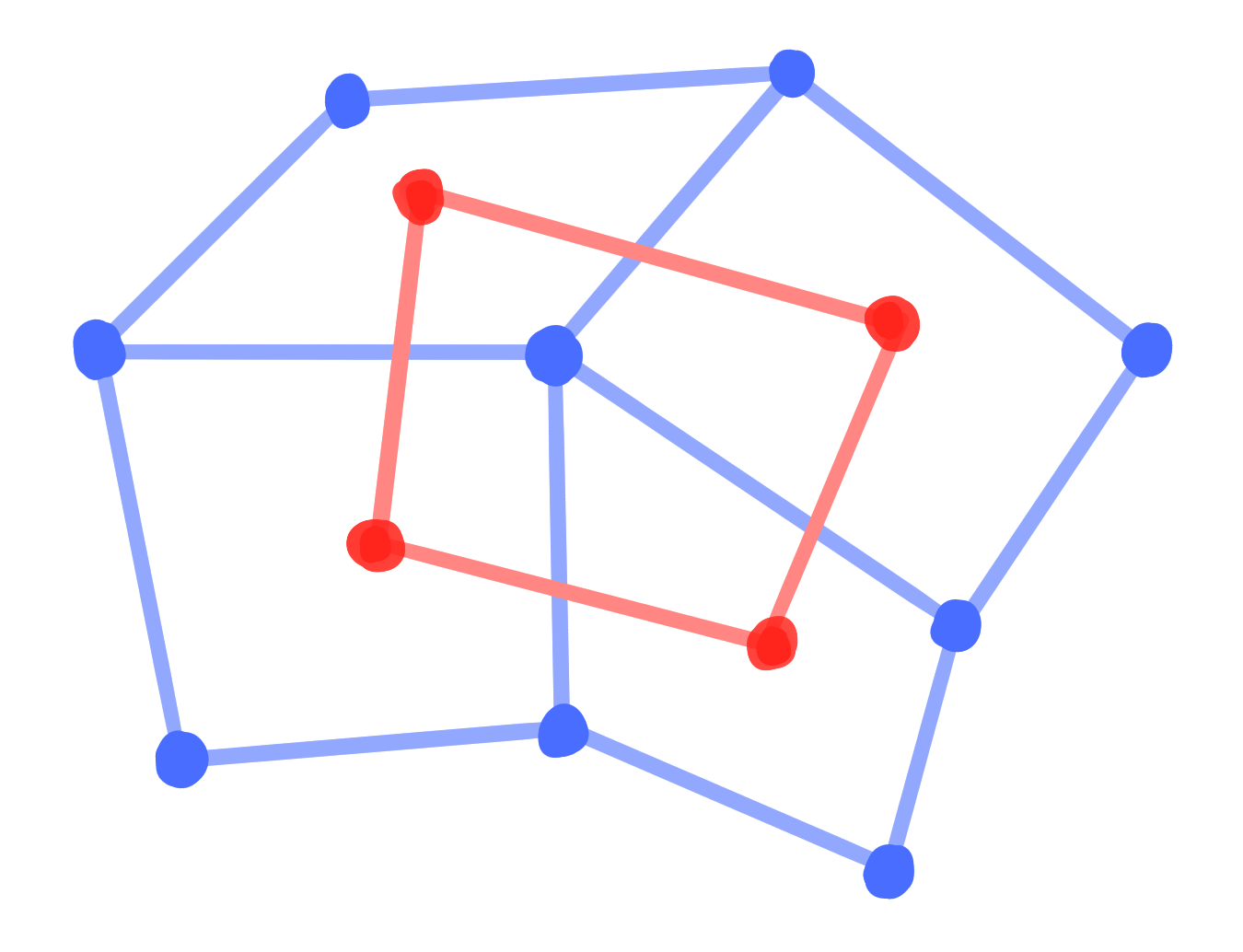
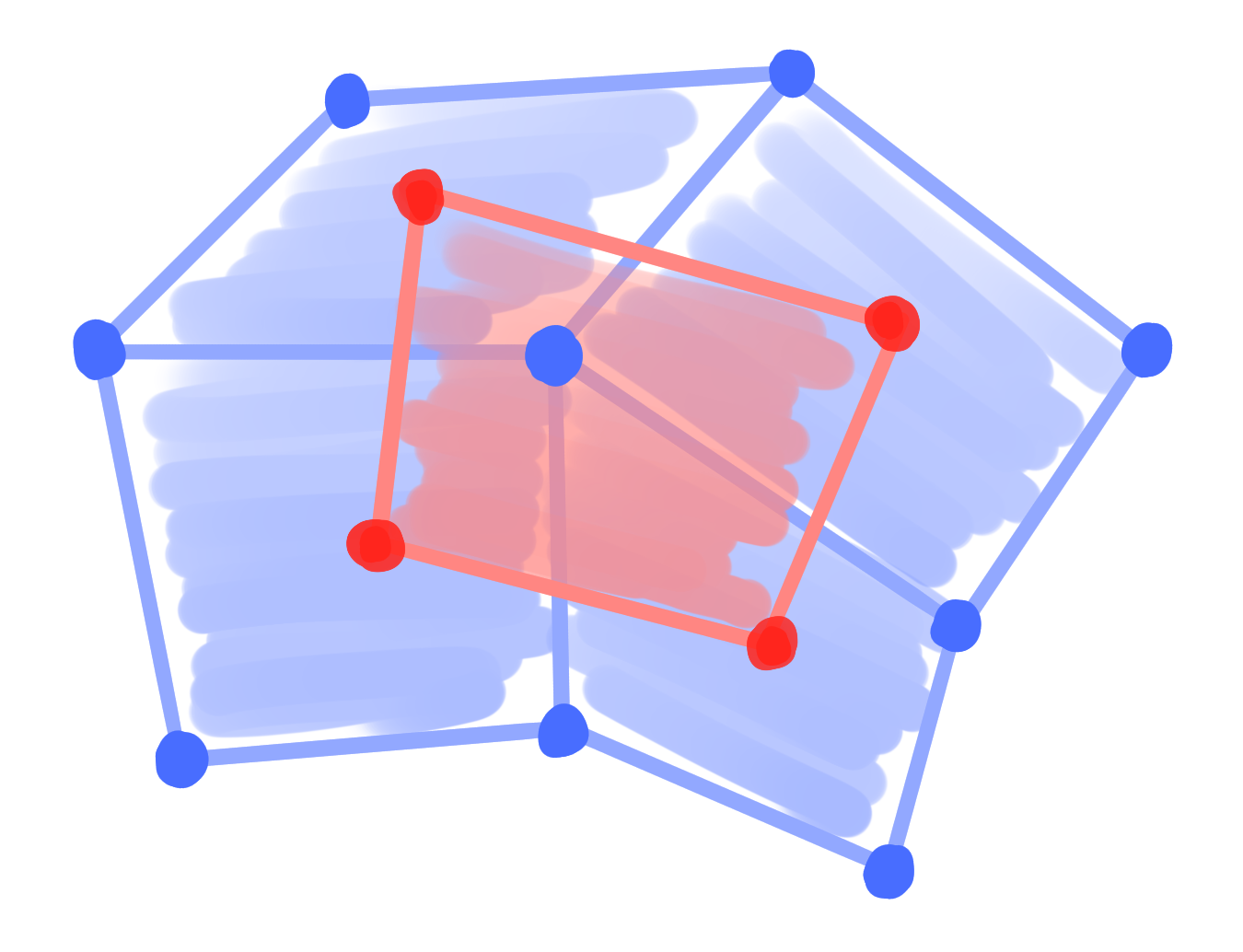
Definition:
A bi*net $~ b : D \rightarrow \mathrm{Planes}(\R^3) ~$ is called conjugate
$\Leftrightarrow$ $b|_V$ and $b|_F$ are Q*-nets.




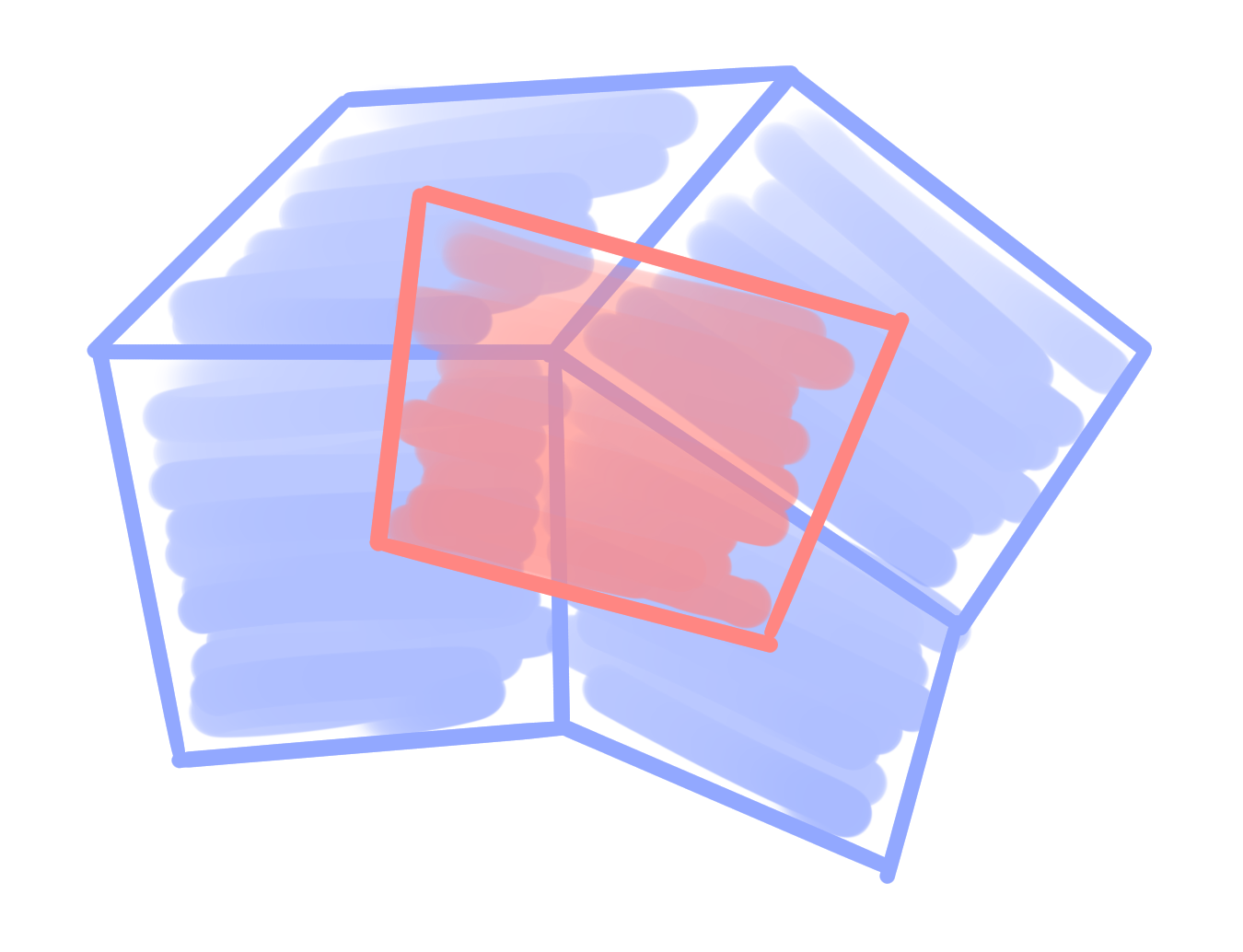
  • Every conjugate binet $b$ defines a conjugate bi*net $\square b$ by
    $ \qquad \square b(d) = \bigvee \{ b(d') ~|~ d' \in D, ~ d' \text{ incident to } d \}, $
  • Vice versa, every conjugate bi*net $b$ defines a conjugate binet $\square^* b$ by
    $ \qquad \square^* b(d) = \bigcap \{ b(d') ~|~ d' \in D, ~ d' \text{ incident to } d \}, $
Principal binets
Definition:
A principal binet $~ b : D \rightarrow \R^3 ~$ is a binet that is both conjugate and orthogonal.

Definition:
A principal bi*net $~ b : D \rightarrow \mathrm{Planes}(\R^3) ~$ is a bi*net that is both conjugate and orthogonal.

Lemma:
Let $~ b : D \rightarrow \R^3 ~$ be a conjugate binet. Then \[ b \text{ orthogonal } \qquad \Leftrightarrow \qquad \square b \text{ orthogonal } \]

Thus, principal binets come in pairs $(b, \square b)$.
Möbius lift of principal binets
Theorem:
Let $~b : D \rightarrow \R^3~$ be a principal binet.
Then its Möbius lift $~b_\mathcal{M} : D \rightarrow \R\mathrm{P}^4~$ is a conjugate polar binet.

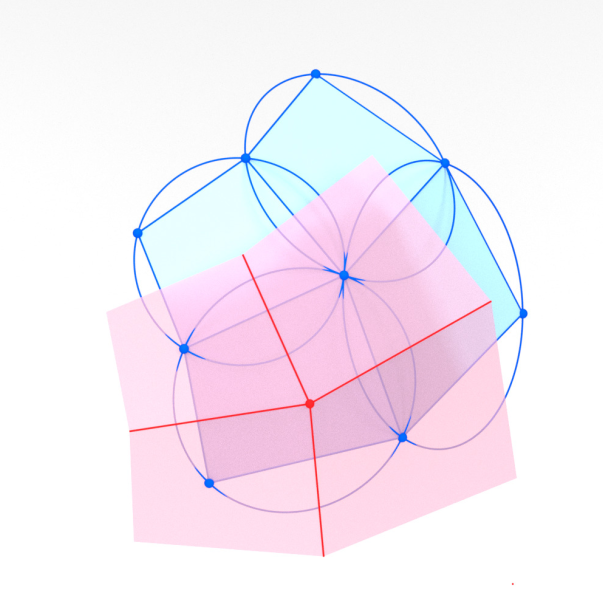
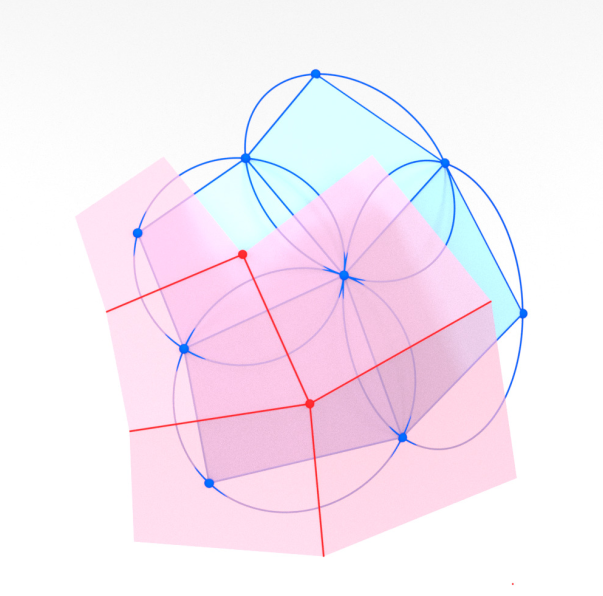
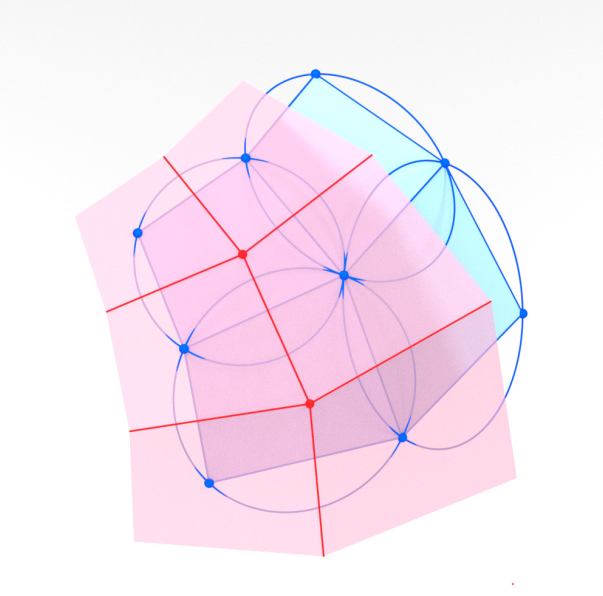
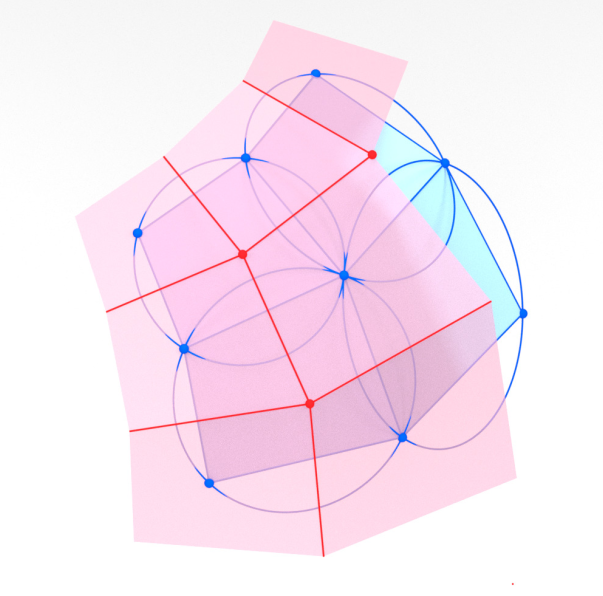
  • Additional structure from planar sections of the Möbius quadric:
    Circle per $d \in D$.
Laguerre lift of principal binets
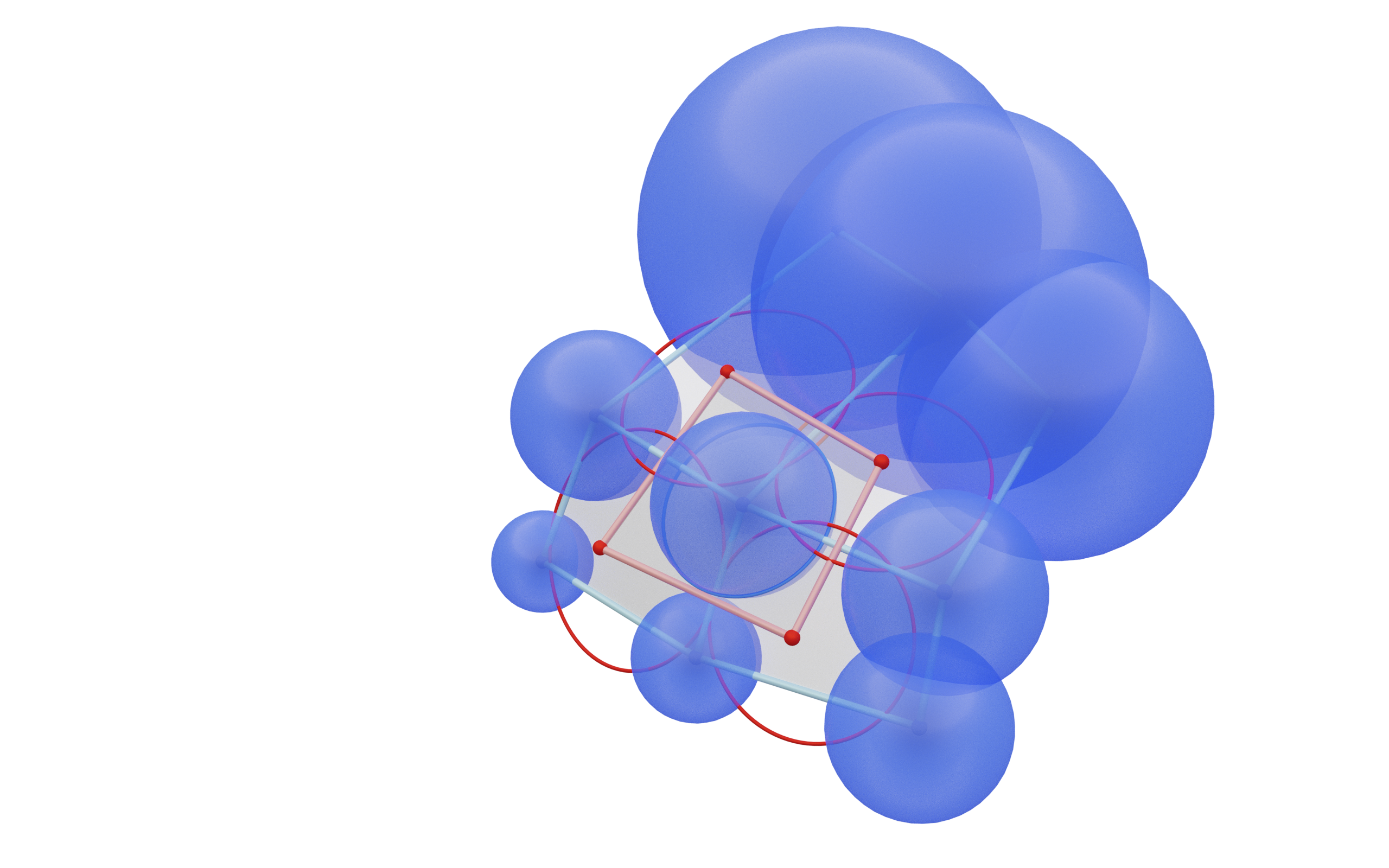
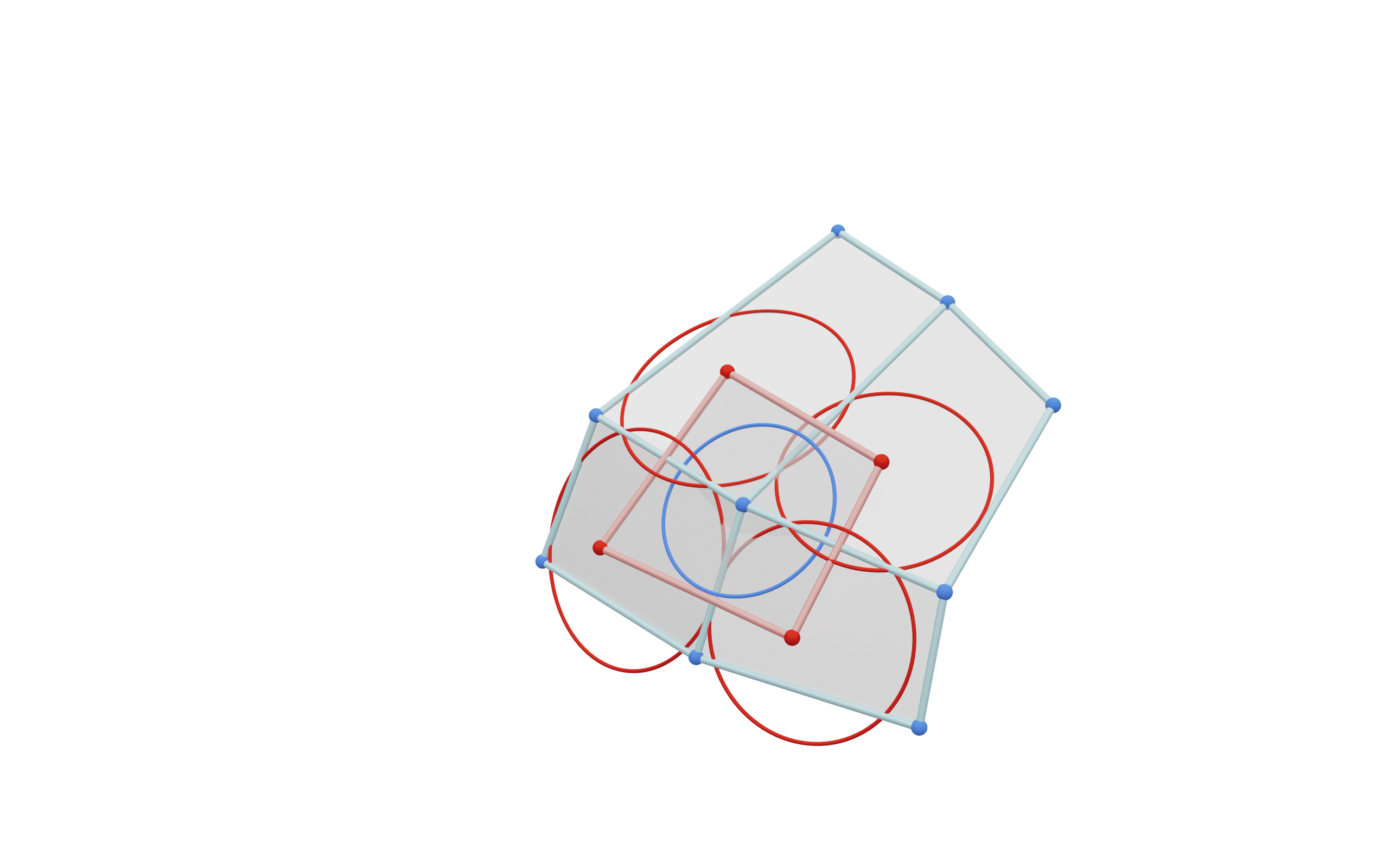
Theorem:
Let $~b : D \rightarrow \mathrm{Planes}(\R^3)~$ be a principal bi*net.
Then its Laguerre lift $~b_\mathcal{B} : D \rightarrow \R\mathrm{P}^4~$ is a conjugate polar binet.

  • Additional structure from planar sections of the Blaschke cylinder:
    Cone per $d \in D$.
Lie lift of principal binets
Combine the Möbius lift of $b$ and the Laguerre lift of $\square b$:
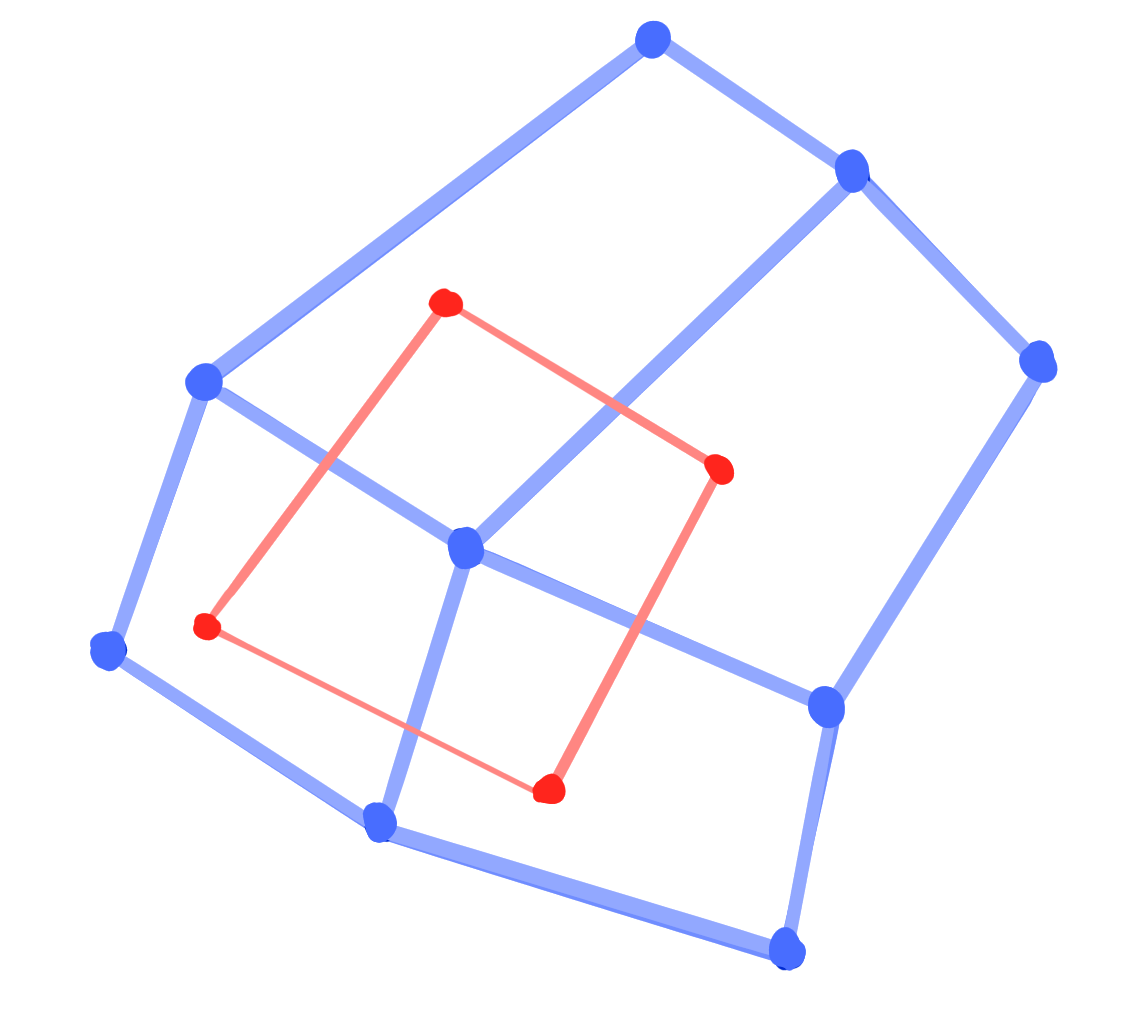
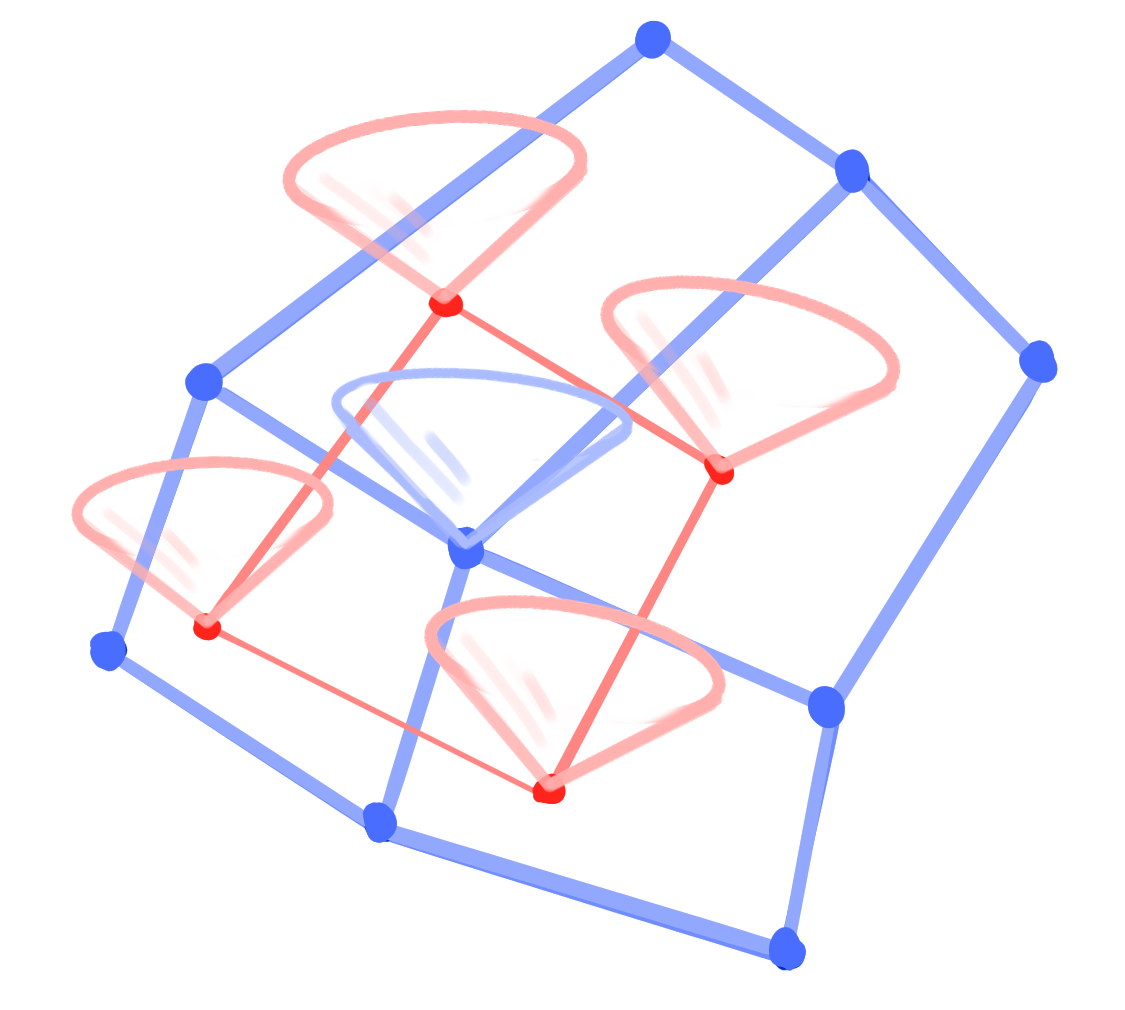
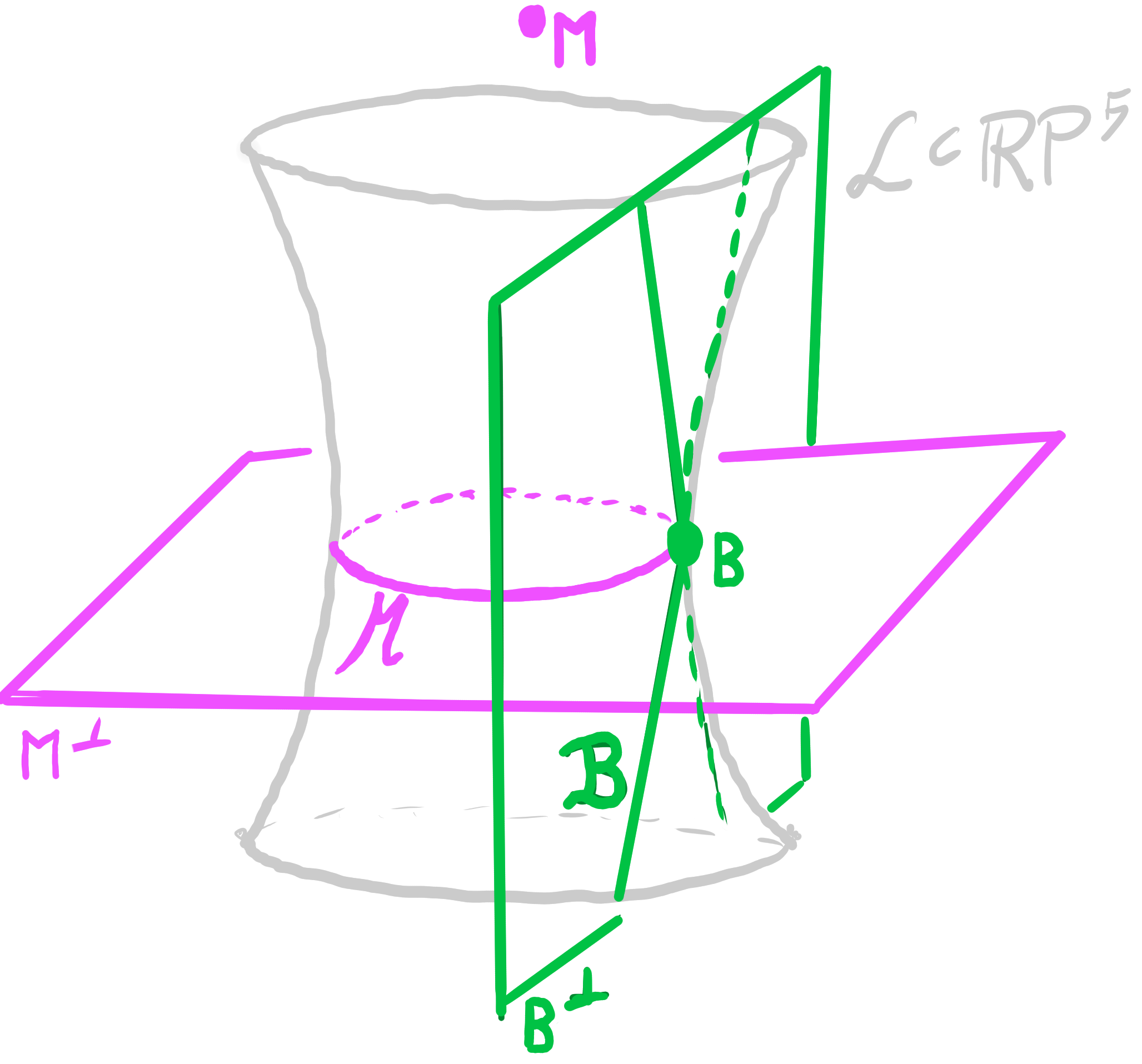
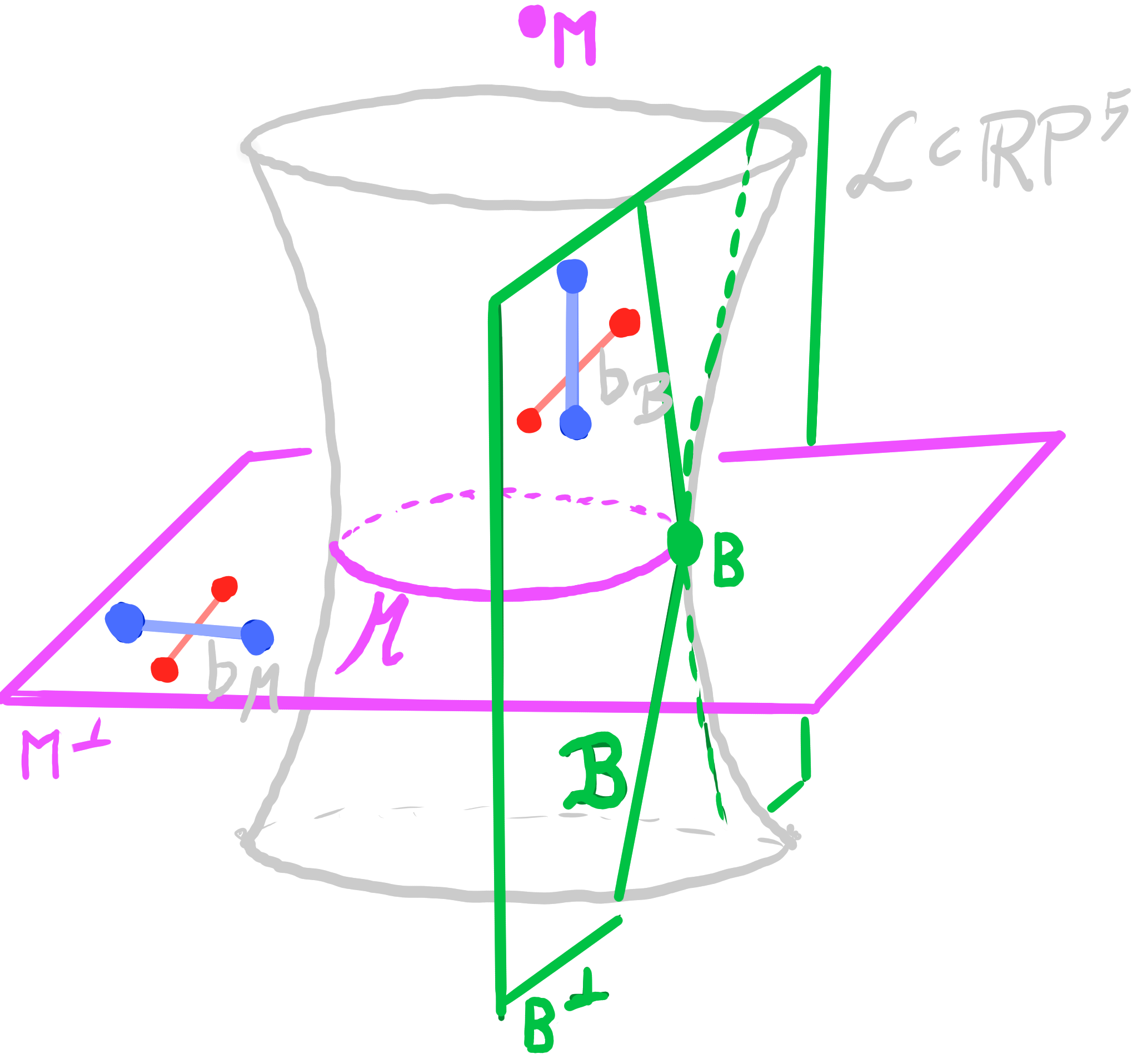
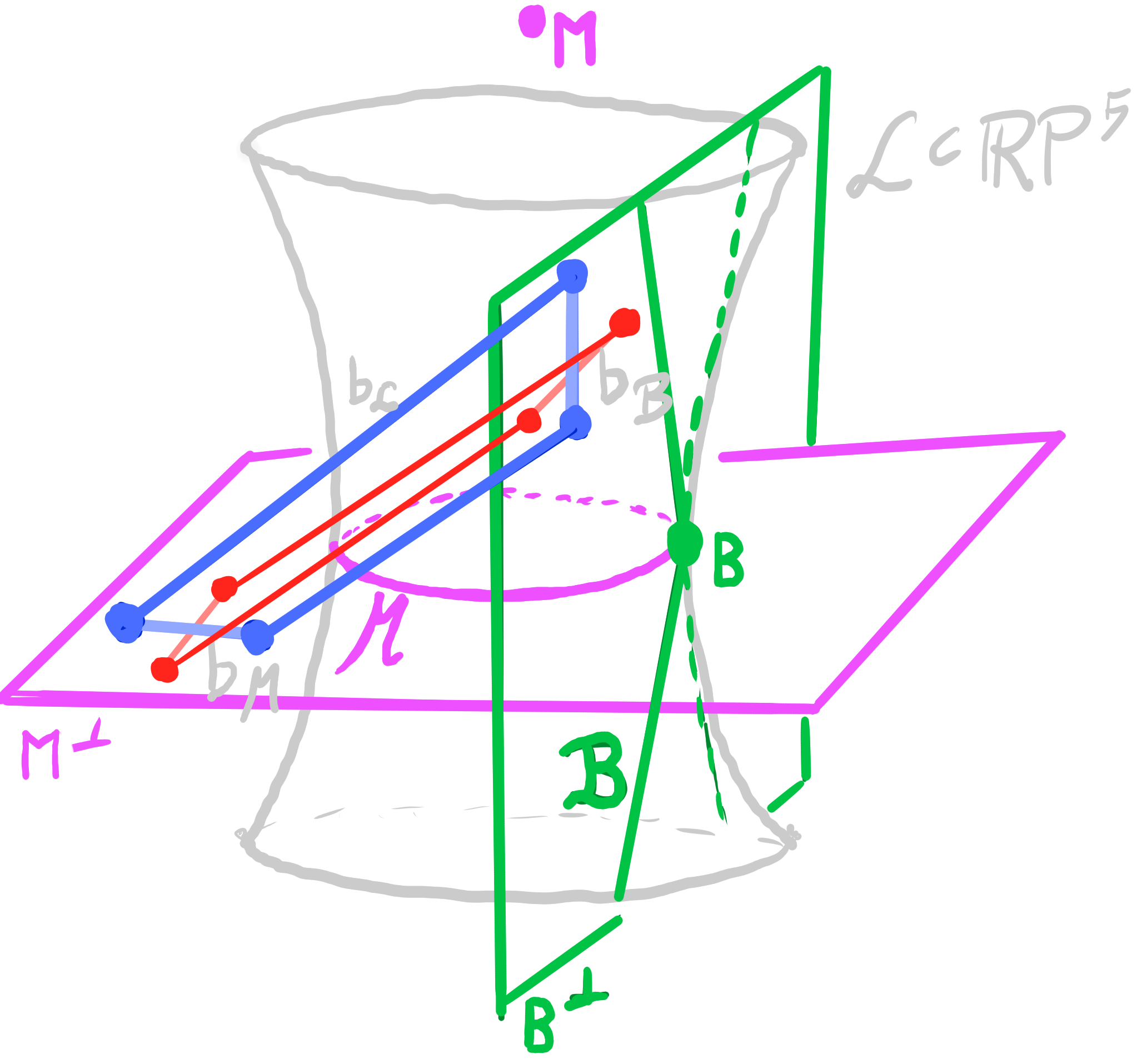
Definition:
Let $\quad b : D \rightarrow \R^3 \quad$ be a principal binet.
Let $\quad b_{\mathcal{M}} : D \rightarrow \mathbf{M}^\perp \subset \R\mathrm{P}^5 \quad$ be a Möbius lift of $b$,
and $\quad b_{\mathcal{B}} : D \rightarrow \mathbf{B}^\perp \subset \R\mathrm{P}^5 \quad$ be a Laguerre lift of $\square b$.
Then the map $\quad b_{\mathcal{L}} = b_{\mathcal{M}} \vee b_{\mathcal{B}} : D \rightarrow \mathrm{Lines}(\R\mathrm{P}^5) \quad$ is called a Lie lift of $b$.
Theorem:
The Lie lift $~ b_{\mathcal{L}} : D \rightarrow \left\{\text{lines in } \R P^5\right\} ~$ of a principal binet satisfies:
  • adjacent lines intersect
  • $b_{\mathcal{L}}(v) \perp b_{\mathcal{L}}(f) \quad$ for incident $v \in V$ and $f \in F$

Remark:
The central projection of the lines of the Lie lift to $\R^3$ with center $\mathbf{M} \vee \mathbf{B}$ yields the normal bicongruence of the principal binet.

Conclusion:
Principal binets in $\R^3$ can be lifted to polar line bicongruences in $\R\mathrm{P}^5$.
Vice versa, polar line bicongruences in $\R\mathrm{P}^5$ project to principal binets in $\R^3$.
Geometric representation of the lines of the Lie lift.
Summary: Geometry of principal binets
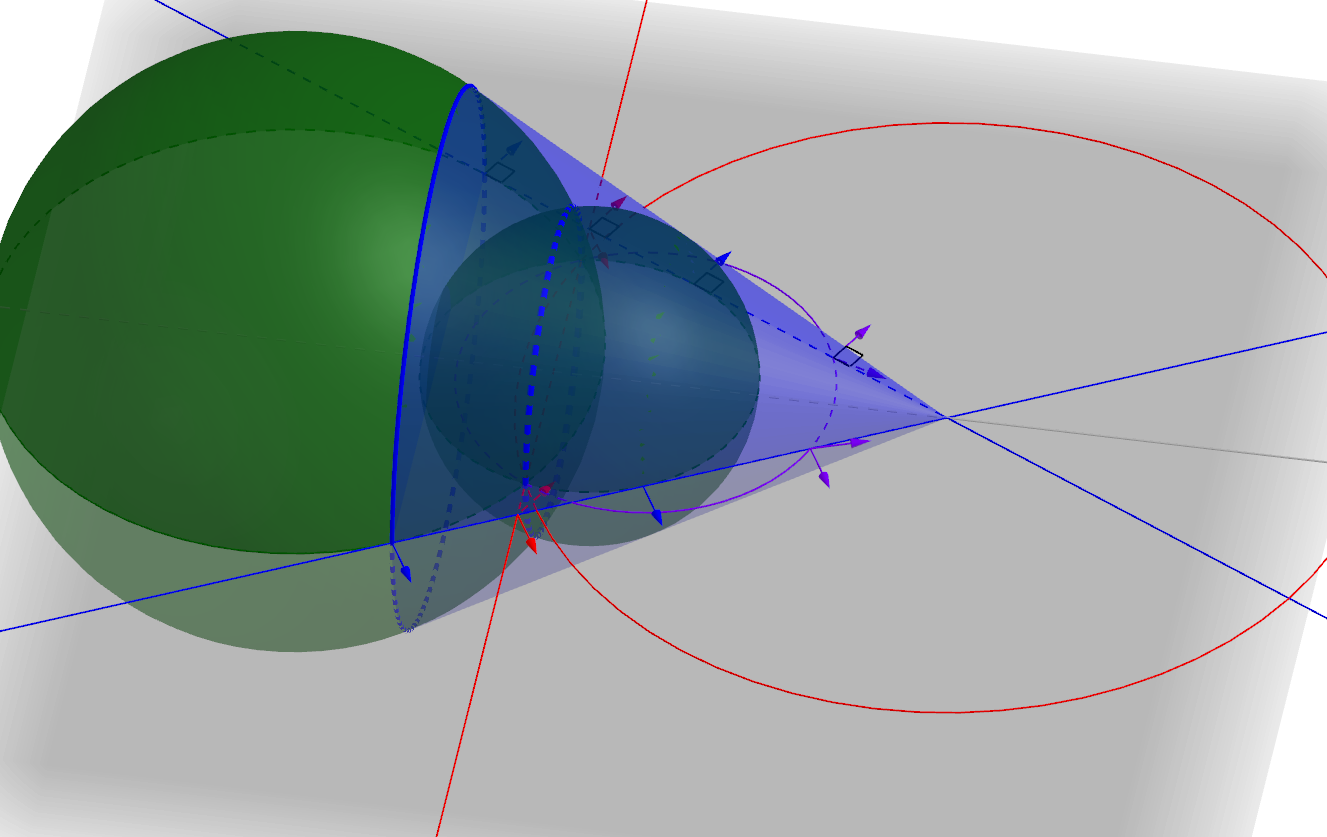
  • Generalize circular nets (Möbius geometry) and conical nets (Laguerre geometry).
  • Allow Möbius and Laguerre invariant descriptions in terms of polar binets.
  • Allow Lie invariant descriptions in terms of polar bicongruences.


Remark:
  • Binets allow for a natural definition of Koenigs nets, including Christoffel duality.
  • Combining Koenigs binets with orthogonal binets yields isothermic binets.

Part 2: Consistency

Binets on $\Z^N$
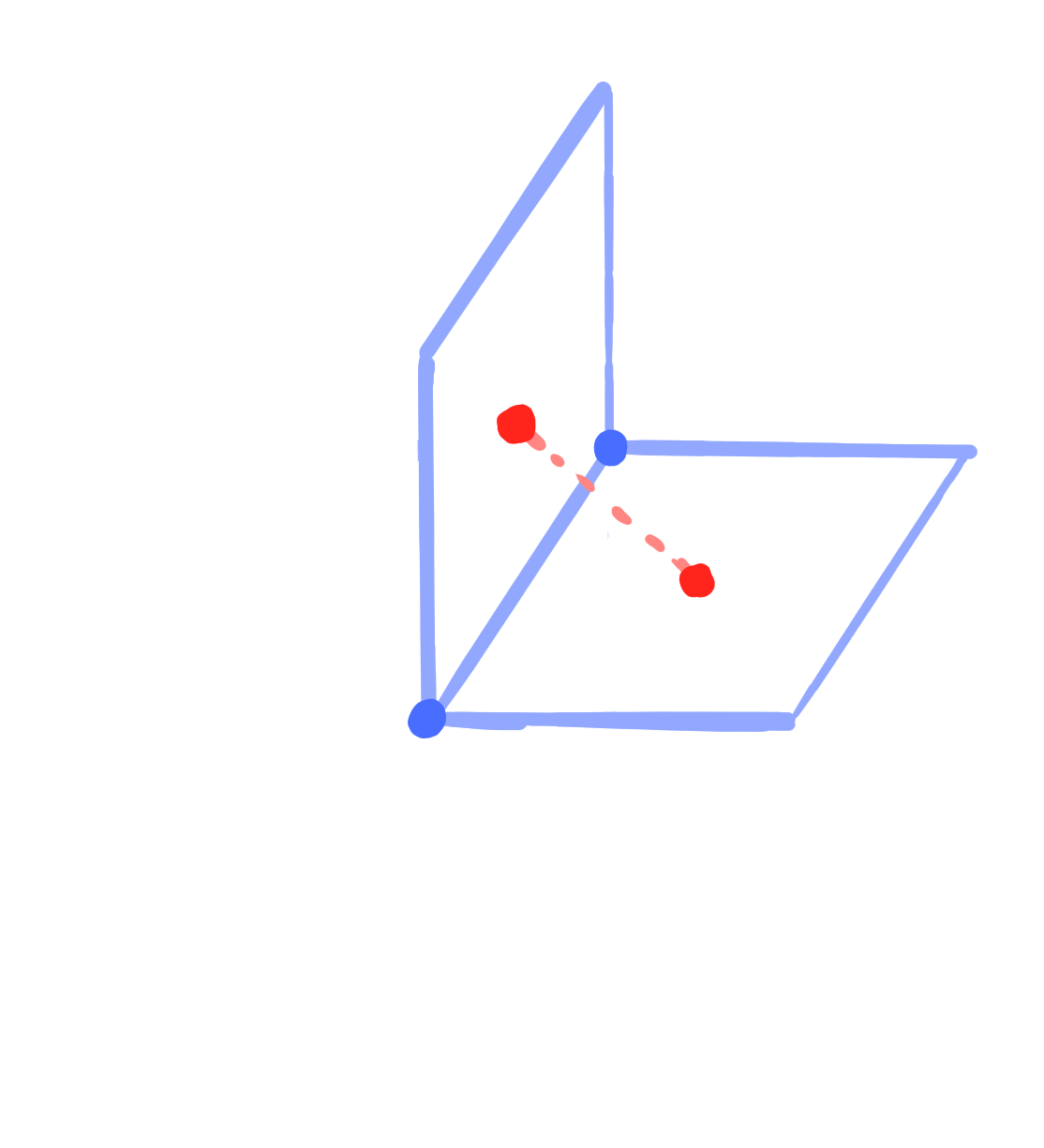
  • $V_N = V(\Z^N) = \Z^N$
  • $E_N = E(\Z^N)$
  • $F_N = F(\Z^N)$
  • $D_N = V_N \cup F_N$
  • $C_N = \left\{ (v, f, v', f') ~|~ v,v'\in V_N,\quad f, f'\in F_N,\quad v, v' \text{ incident to } f, f' \right\}$
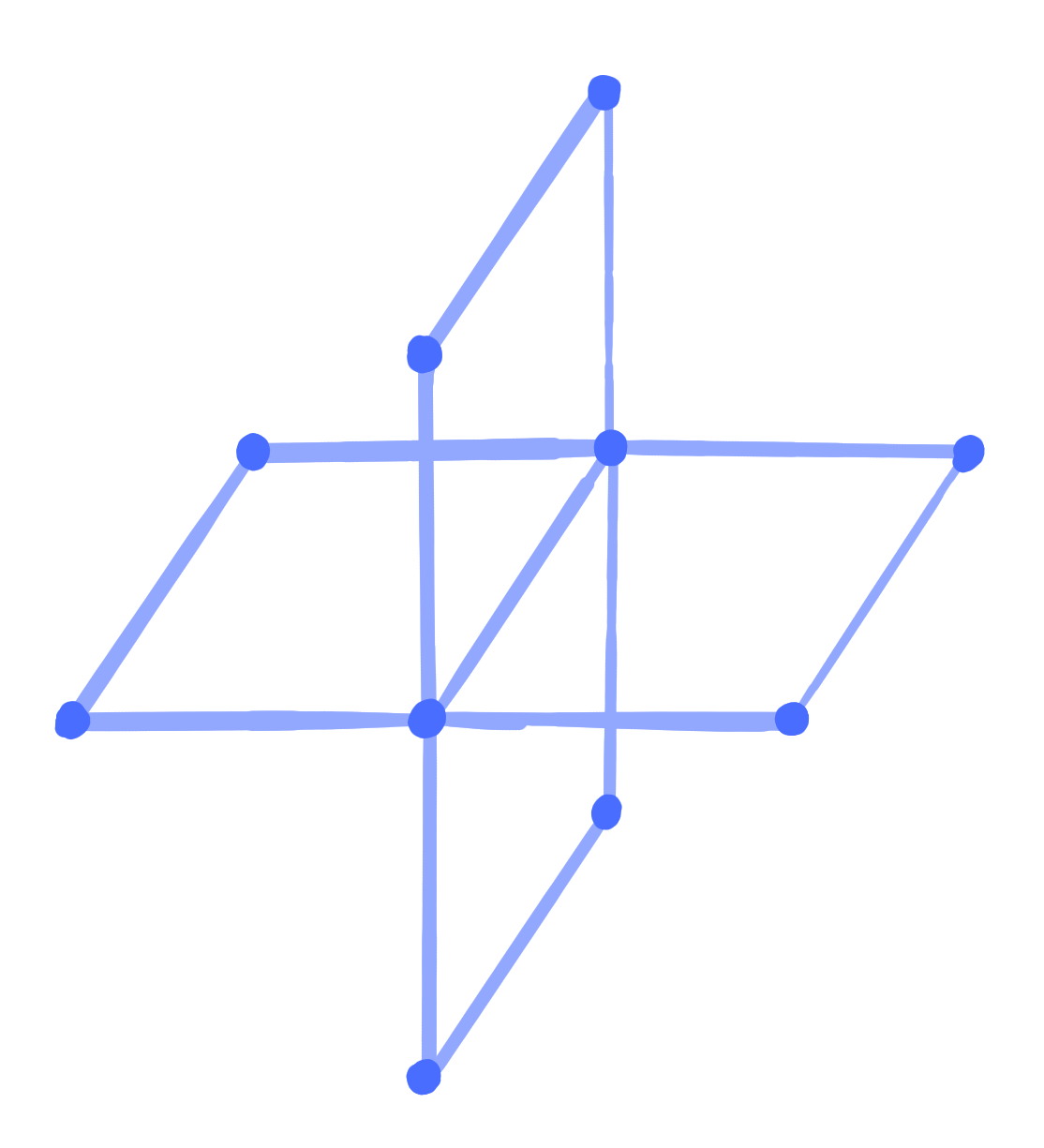
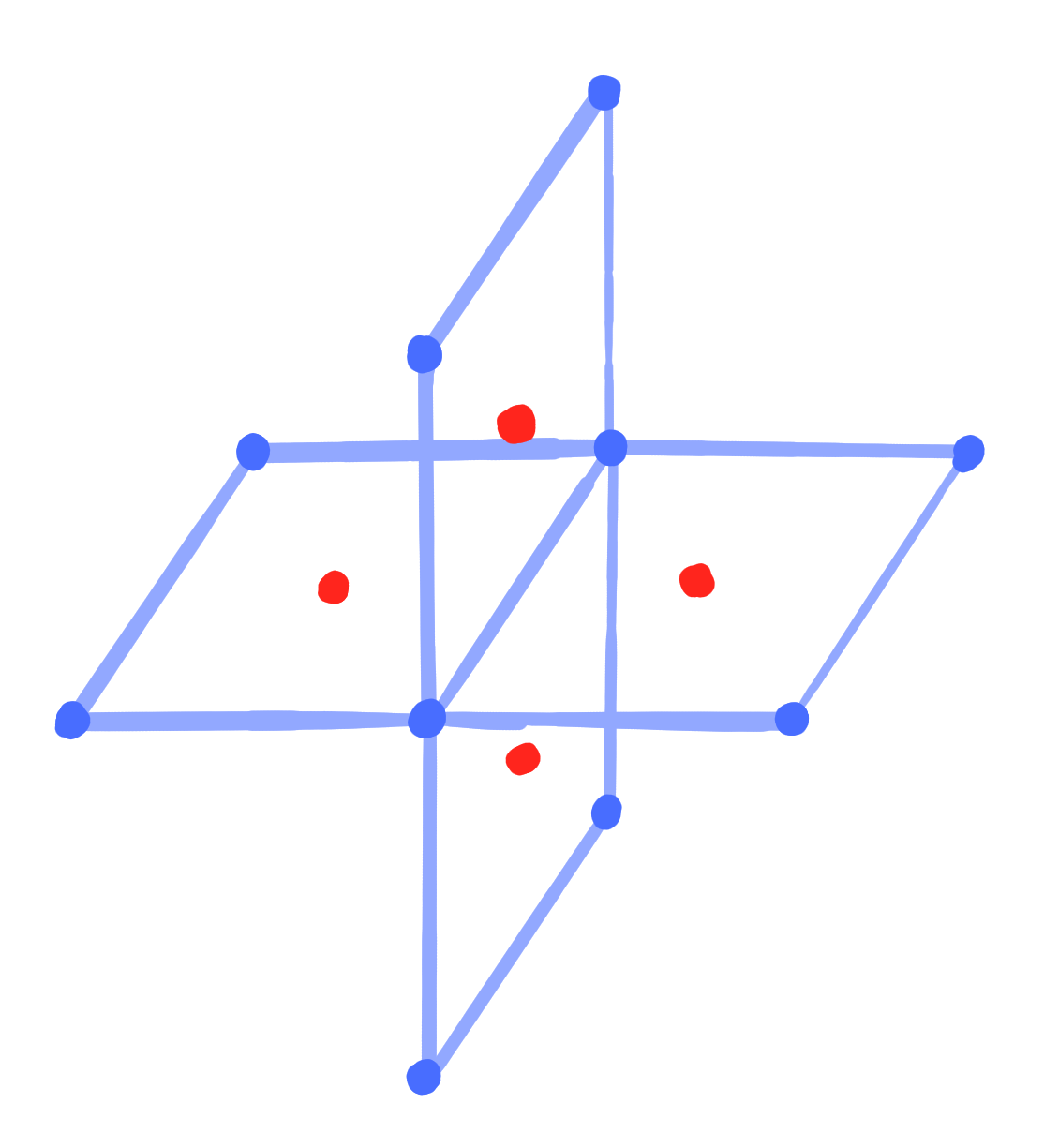
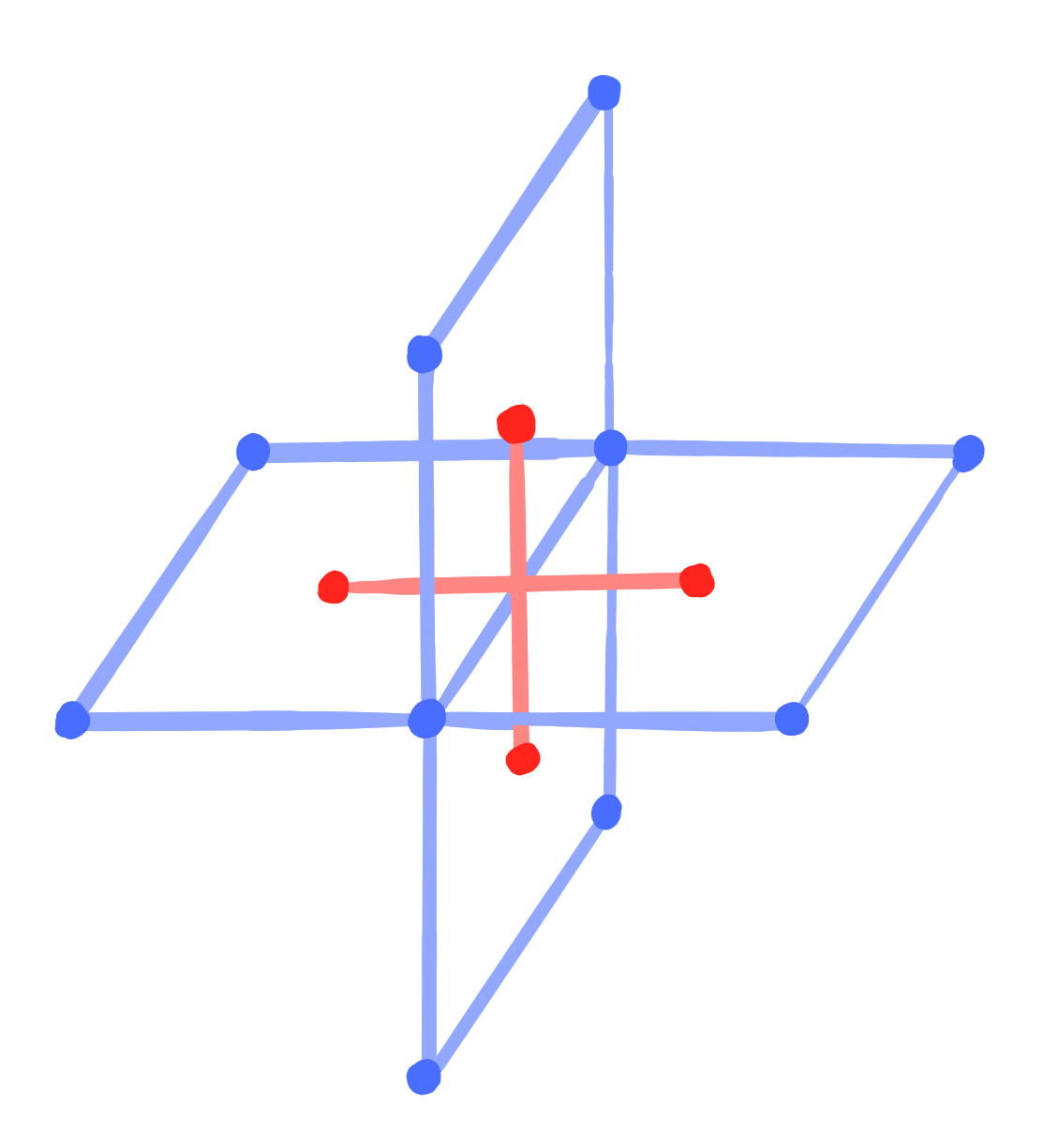
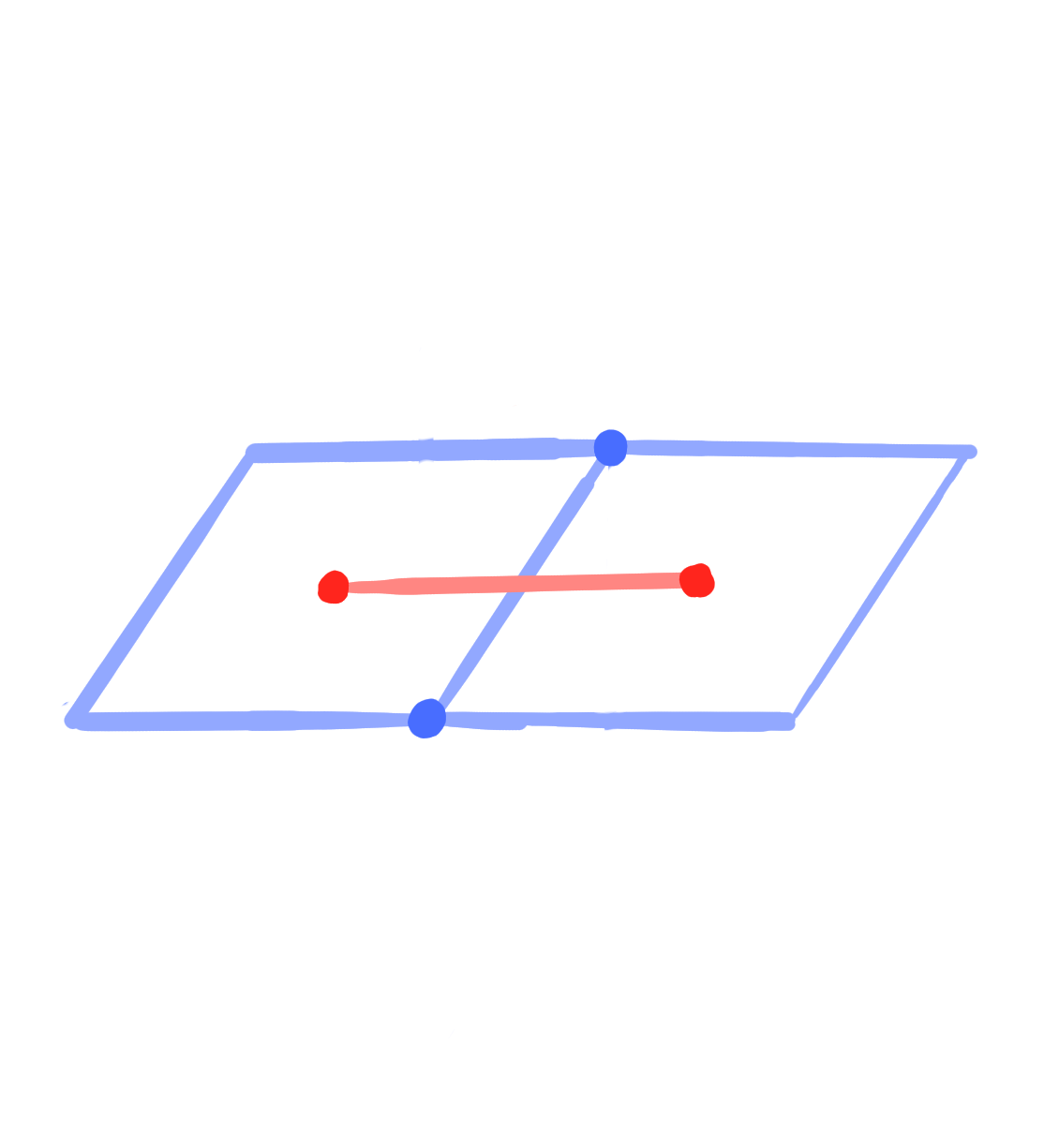
  • An $N$-dimensional vertex-net is a map $~V_N \rightarrow \R\mathrm{P}^n$.
  • An $N$-dimensional face-net is a map $~F_N \rightarrow \R\mathrm{P}^n$.
  • An $N$-dimensional binet is a map $~D_N \rightarrow \R\mathrm{P}^n$.
Conjugate binets on $\Z^N$
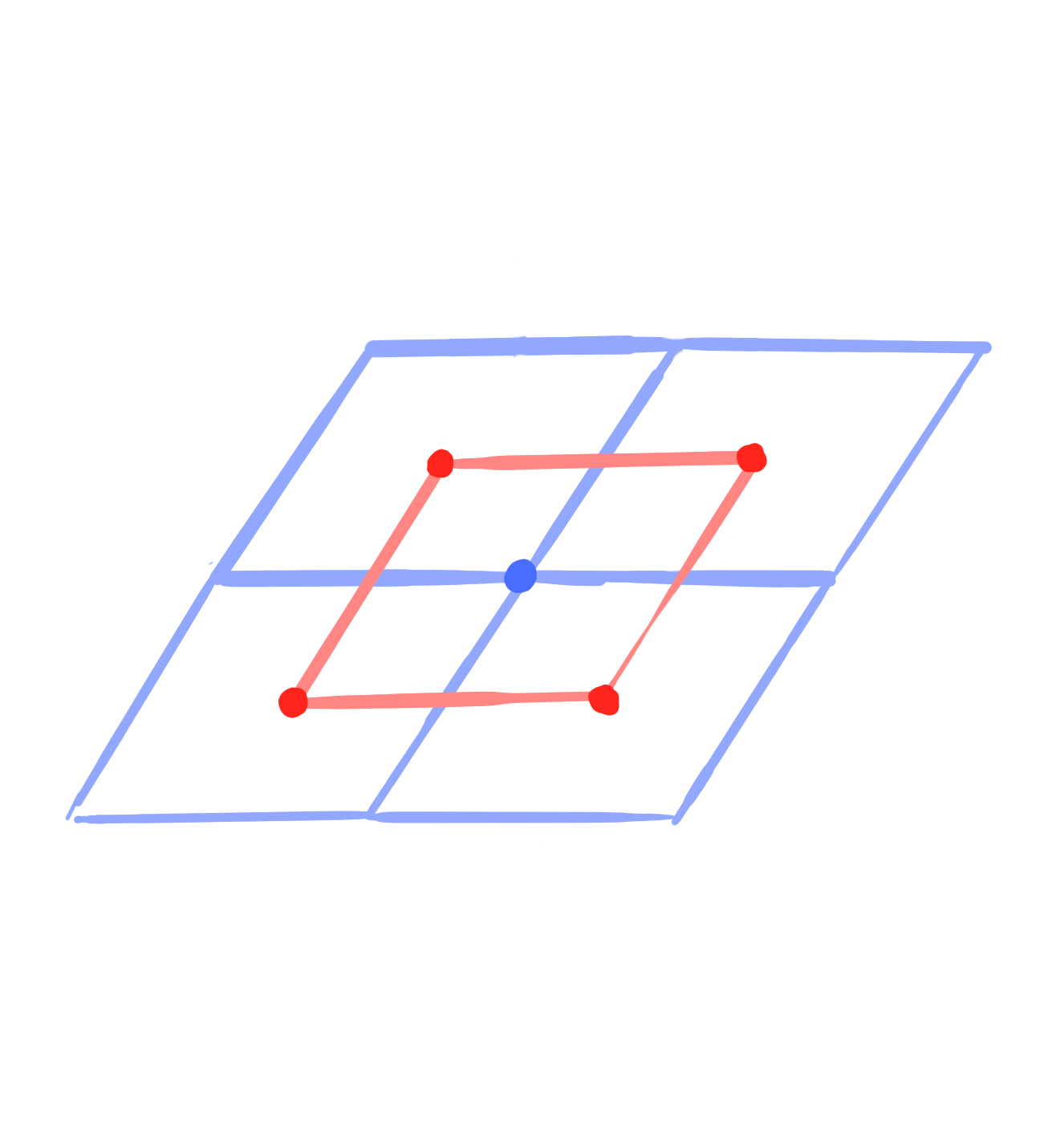
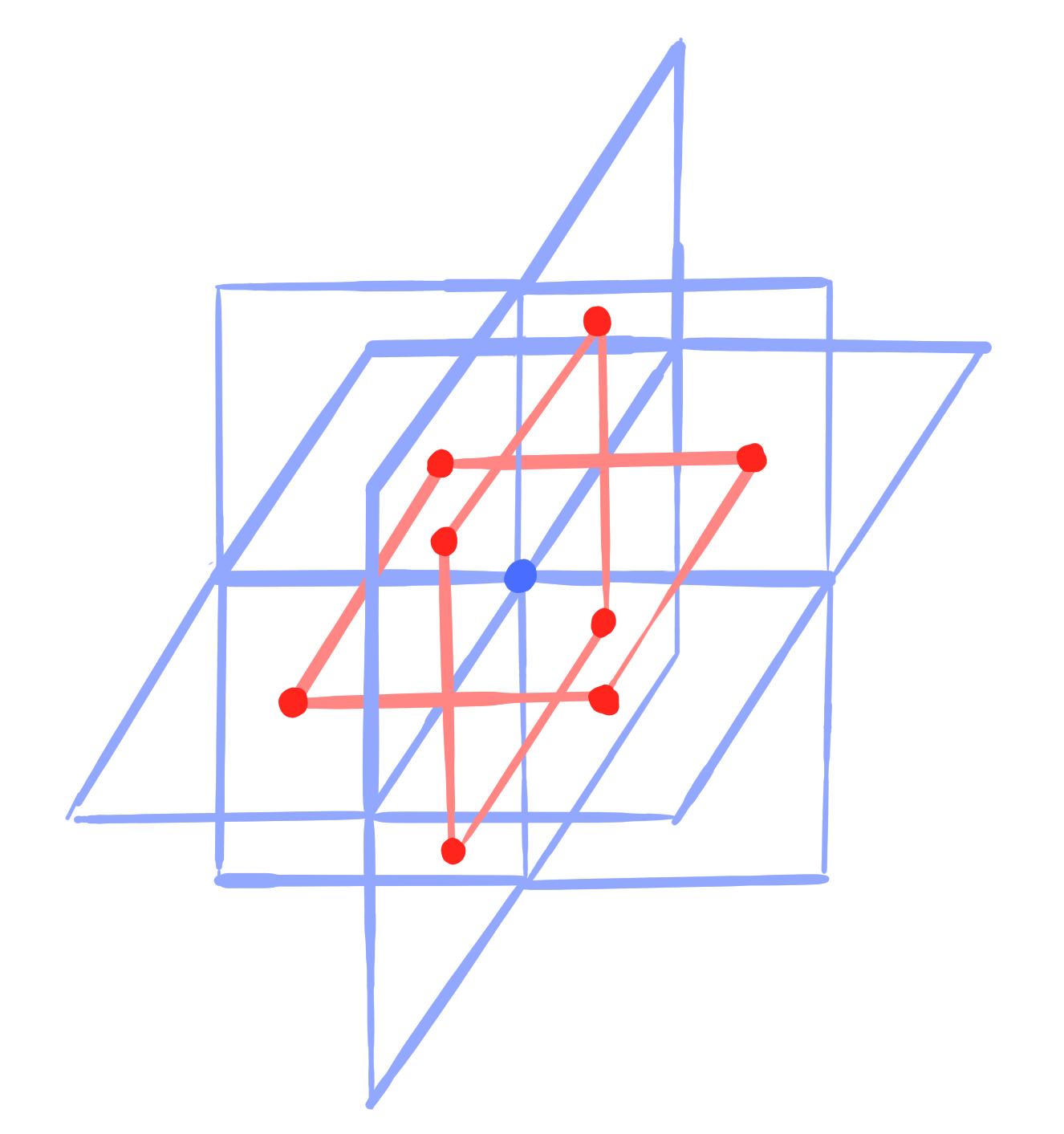
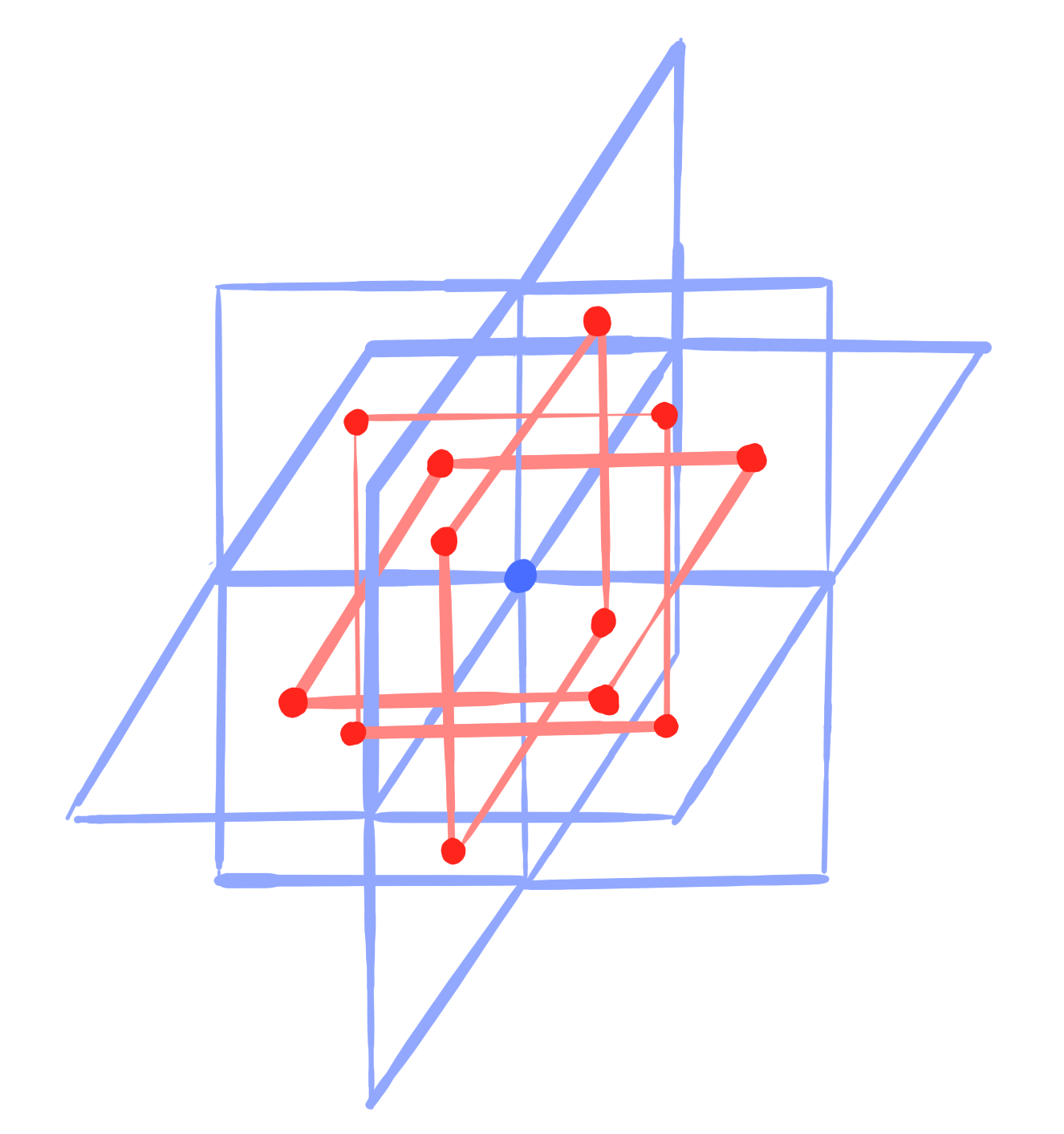
Definition: A conjugate vertex-net (Q-net) is a map $~g : V_N \rightarrow \R\mathrm{P}^n~$ such that
\[ \bigvee_{v \in f} g(v) \quad\text{is a plane for all} ~f \in F_N. \qquad\qquad \]
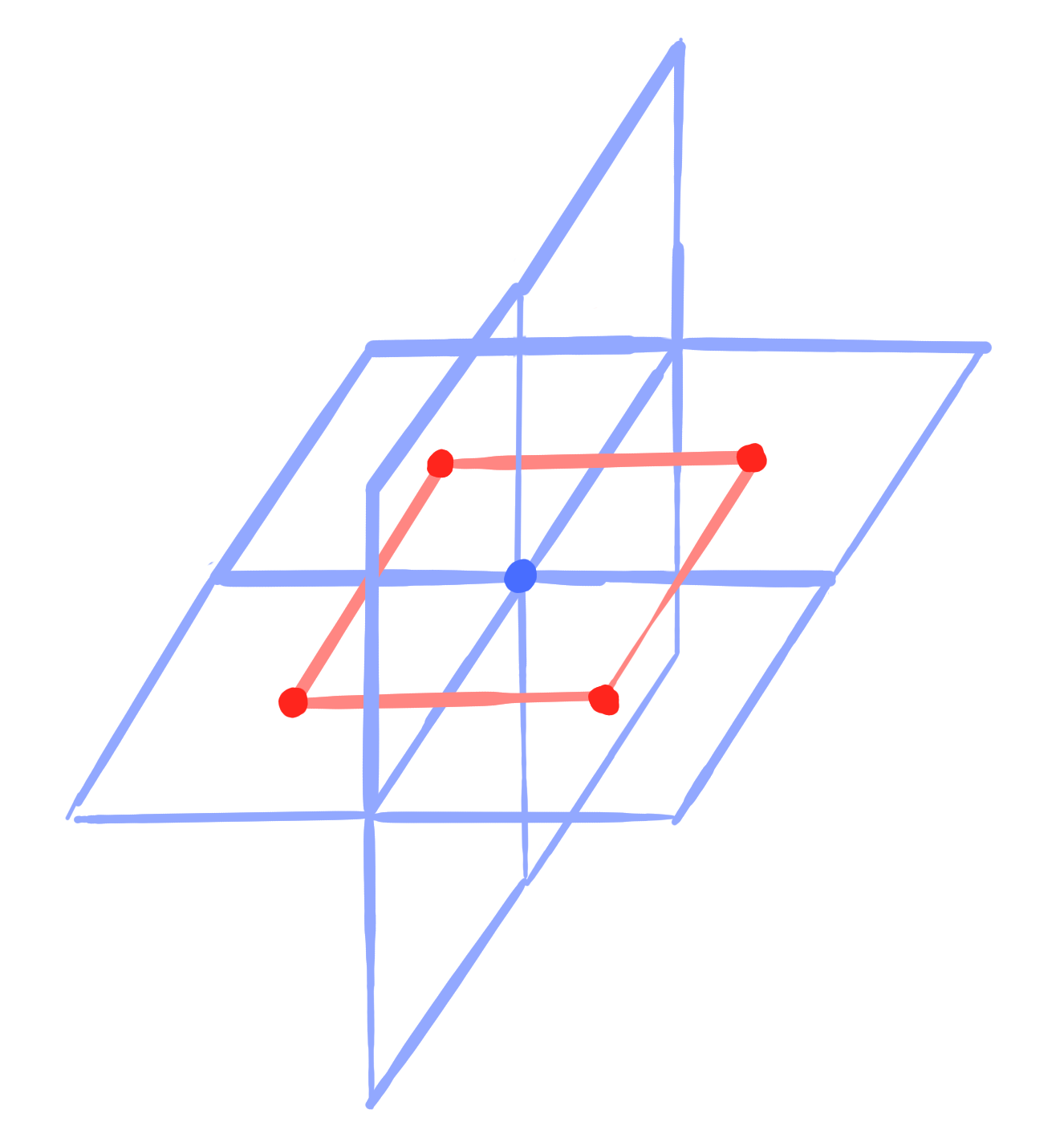
It defines a corresponding map $~\square g : F_N \rightarrow \mathrm{Planes}(\R\mathrm{P}^n)~$.

Definition: A conjugate face-net is a map $~g : F_N \rightarrow \R\mathrm{P}^n~$ such that
\[ \bigvee_{f \ni v} g(f) \quad\text{is a plane for all} ~v \in V_N. \]
It defines a corresponding map $~\square g : V_N \rightarrow \mathrm{Planes}(\R\mathrm{P}^n)~$.
Theorem [DS97]: Conjugate vertex-nets are multi-dimensionally consistent 3D-systems.

Question: Are conjugate face-nets consistent?

Consider the restriction to faces only in a given $i,j$-direction: \[ \small F^{ij}_N = \left\{ \{r, r+e_i, r+e_i+e_j, r+e_j\} \in F_N ~|~ r \in \Z^N \right\} \cong \Z^N \]
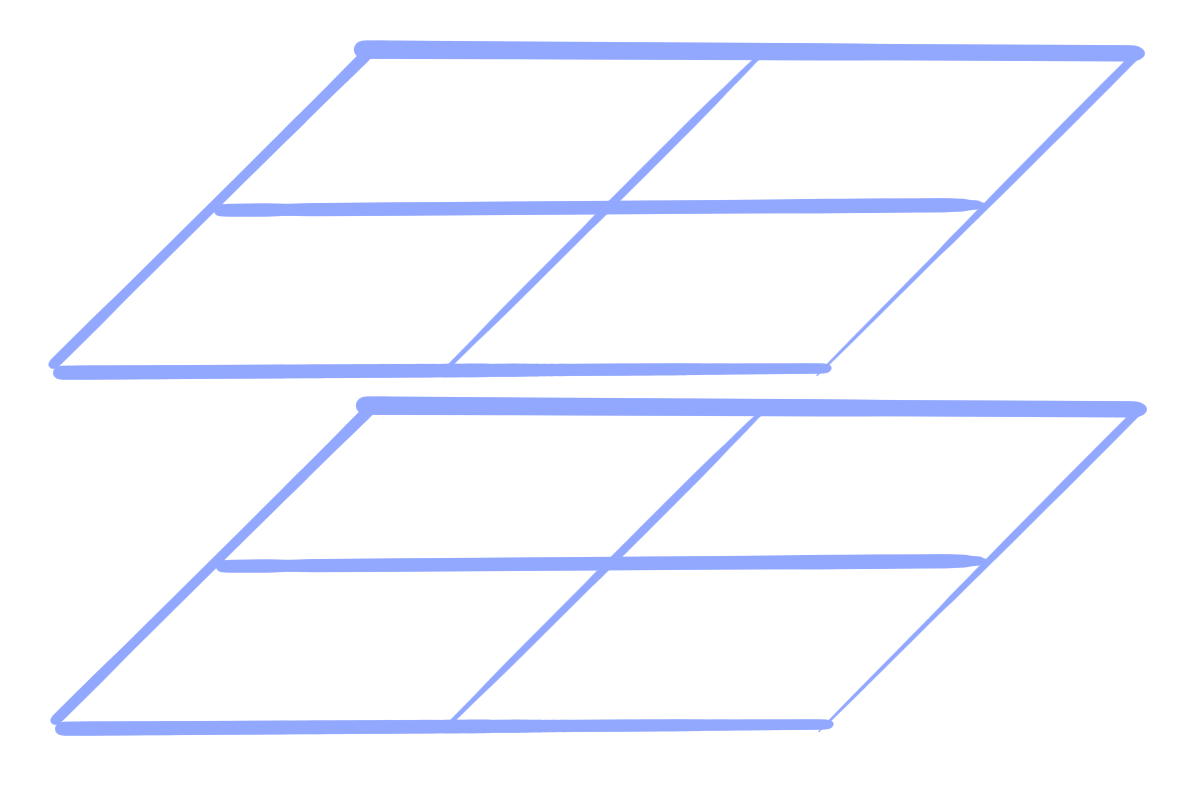
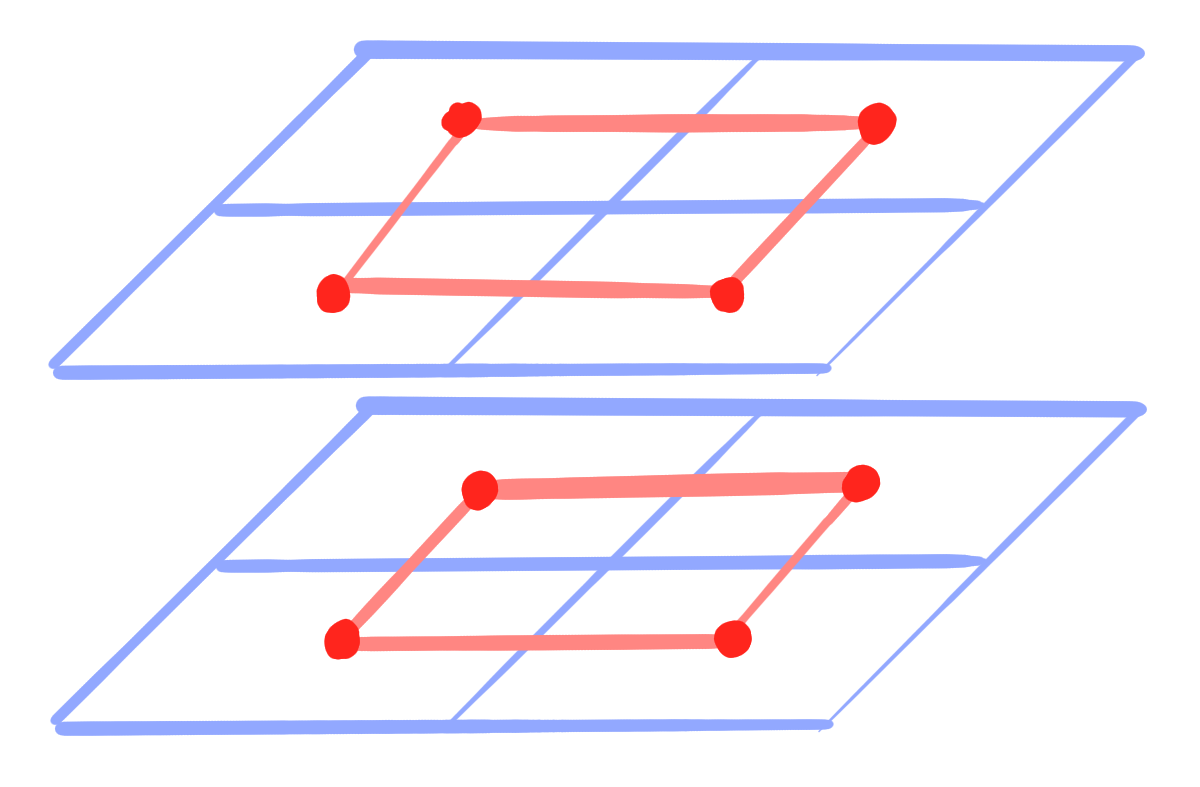
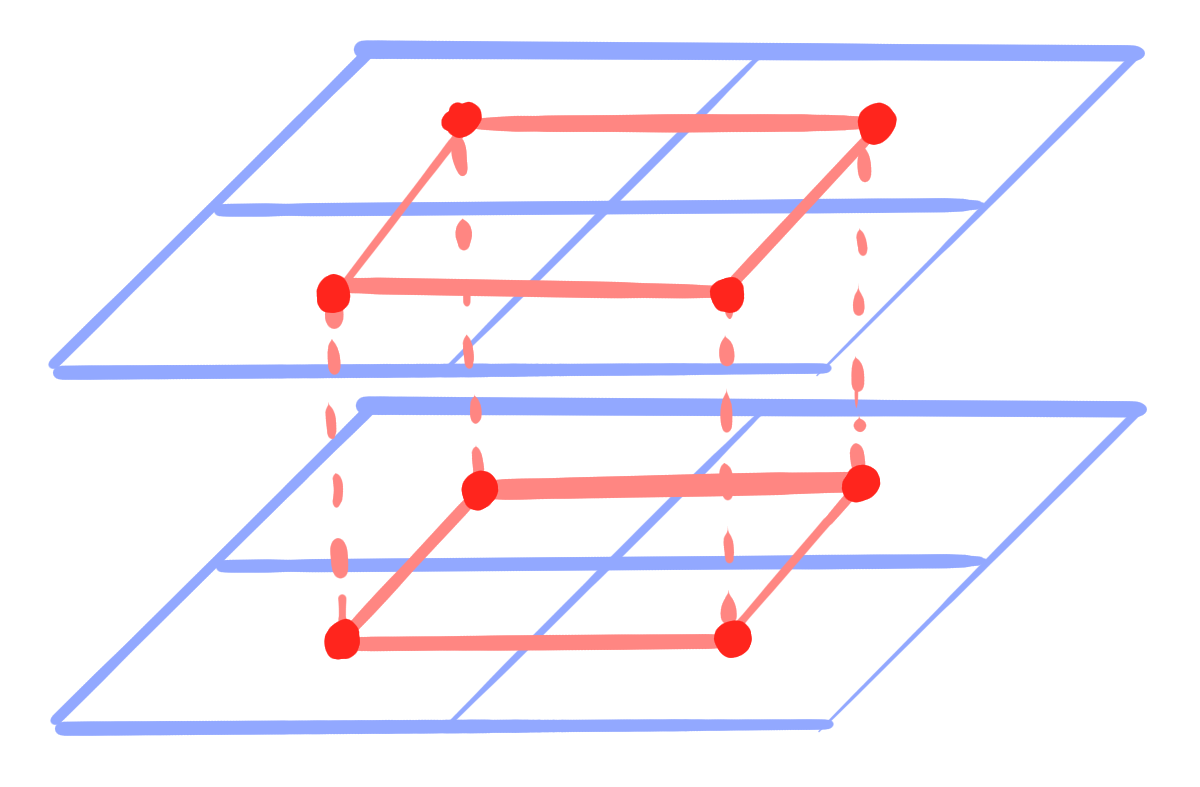
Lemma: Let $g : F_N \rightarrow \R\mathrm{P}^n$ be a conjugate face-net. Then its restriction \[ \small g^{ij} = g|_{F^{ij}_N} : {F^{ij}_N} \cong \Z^N \longrightarrow \R\mathrm{P}^n \] is a conjugate vertex-net.
Vice versa, consider a conjugate vertex-net $~g : F^{ij}_N \rightarrow \R\mathrm{P}^n$.
  • All planes $~\square g : V_N \rightarrow \mathrm{Planes}(\R\mathrm{P}^n)~$ are already defined.
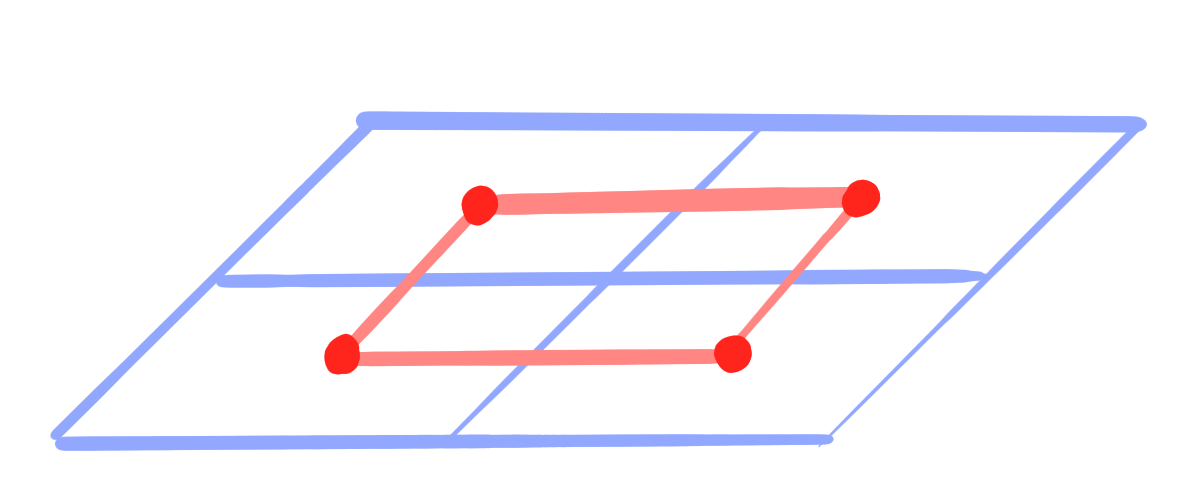
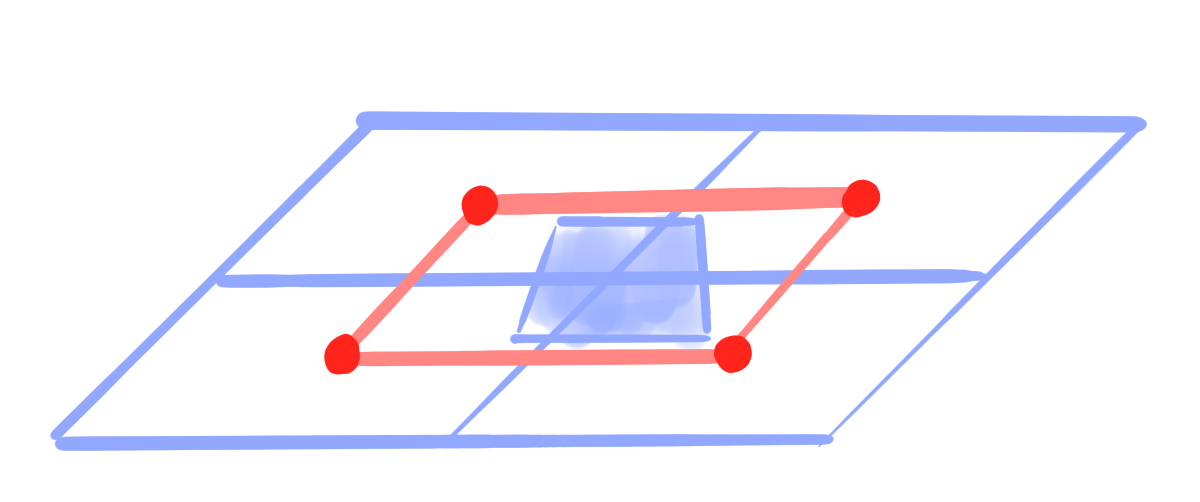
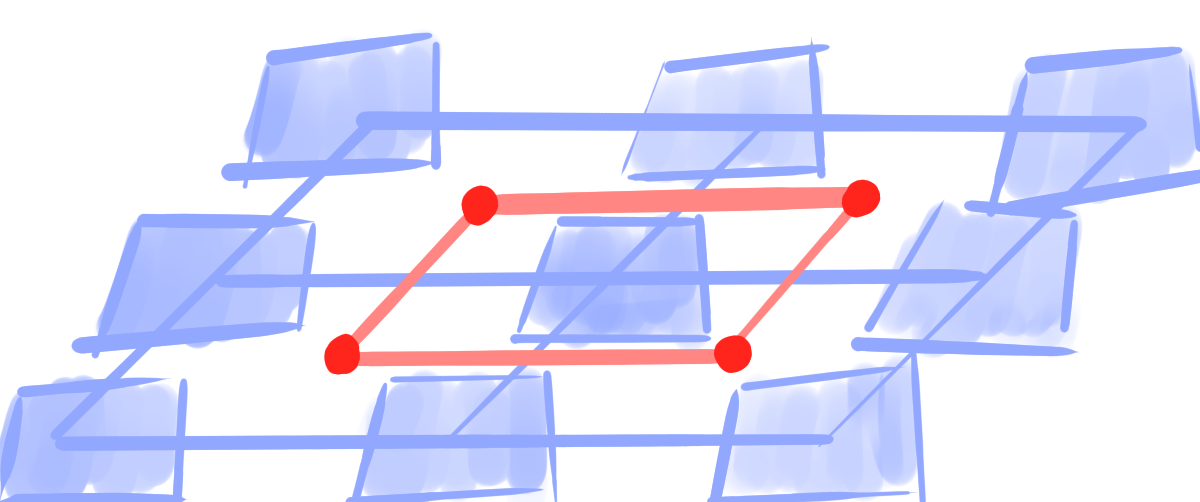
  • The points of the remaining faces can be reconstructed by \[ \small \lceil g \rceil(f) = \bigcap_{v \in f} \square g(v). \]
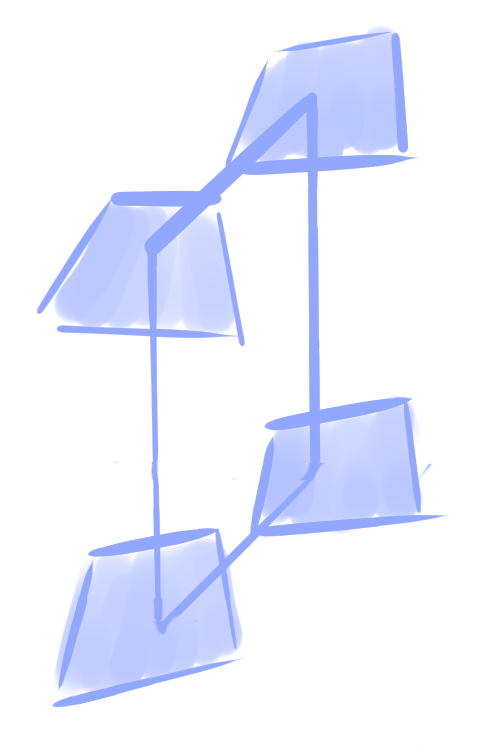
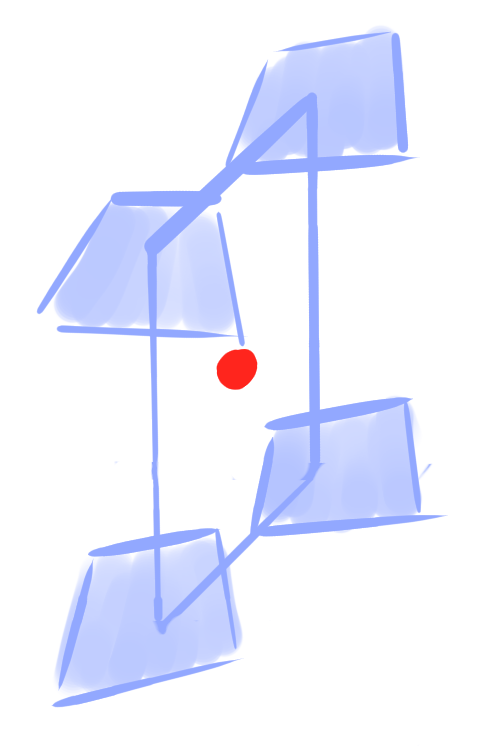
Lemma: Let $~g : F^{ij}_N \rightarrow \R\mathrm{P}^n~$ be a conjugate vertex-net. Then there exists a unique conjugate face-net $~\lceil g \rceil : F_N \rightarrow \R\mathrm{P}^n~$ that restricts to $g$ on $F^{ij}_N$.
Bijection: conjugate face-nets on $F_N$ $~\longleftrightarrow~$ conjugate vertex-nets on $F_N^{ij}$


Theorem: Conjugate face-nets are multi-dimensionally consistent 3D-systems.


Definition:
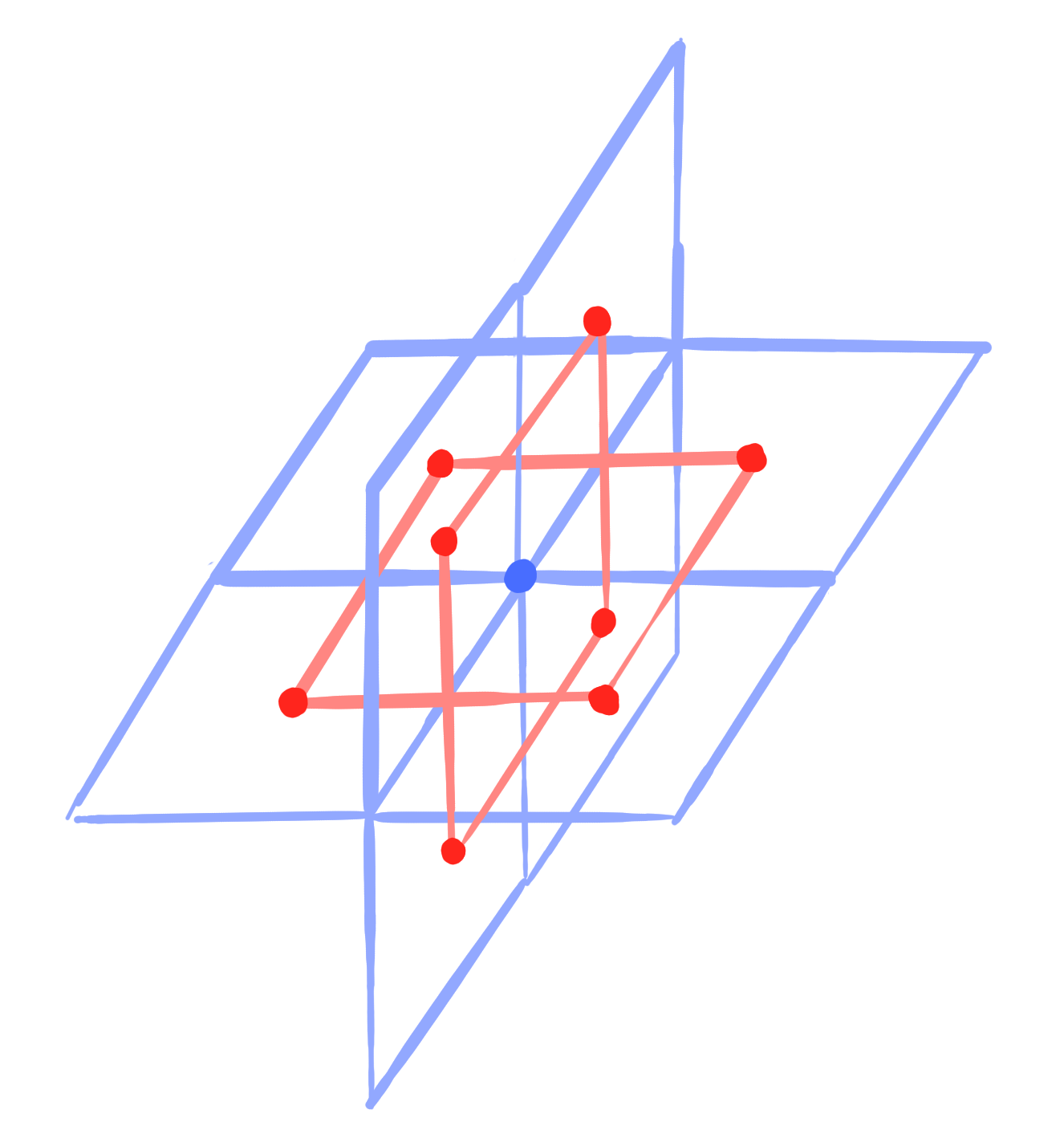
A conjugate binet is a map $~b : D_N \rightarrow \R\mathrm{P}^n~$ such that
$b|_{V_N}$ is a conjugate vertex-net and $b|_{F_N}$ is a conjugate face-net.
It defines a corresponding map $~\square g : D_N \rightarrow \mathrm{Planes}(\R\mathrm{P}^n)~$.


Theorem: Conjugate binets are multi-dimensionally consistent 3D-systems.
Polar conjugate binets on $\Z^N$
Definition: Let $\mathcal{Q} \subset \R\mathrm{P}^n$ be a quadric.
A polar binet is a map $~ b : D_N \rightarrow \R\mathrm{P}^n ~$ such that \[ \small b(v) \perp b(f) \qquad \text{for all incident} ~ v \in V_N, f \in F_N \]
        
Theorem: Polar conjugate binets are a consistent reduction of conjugate binets.
Proof:
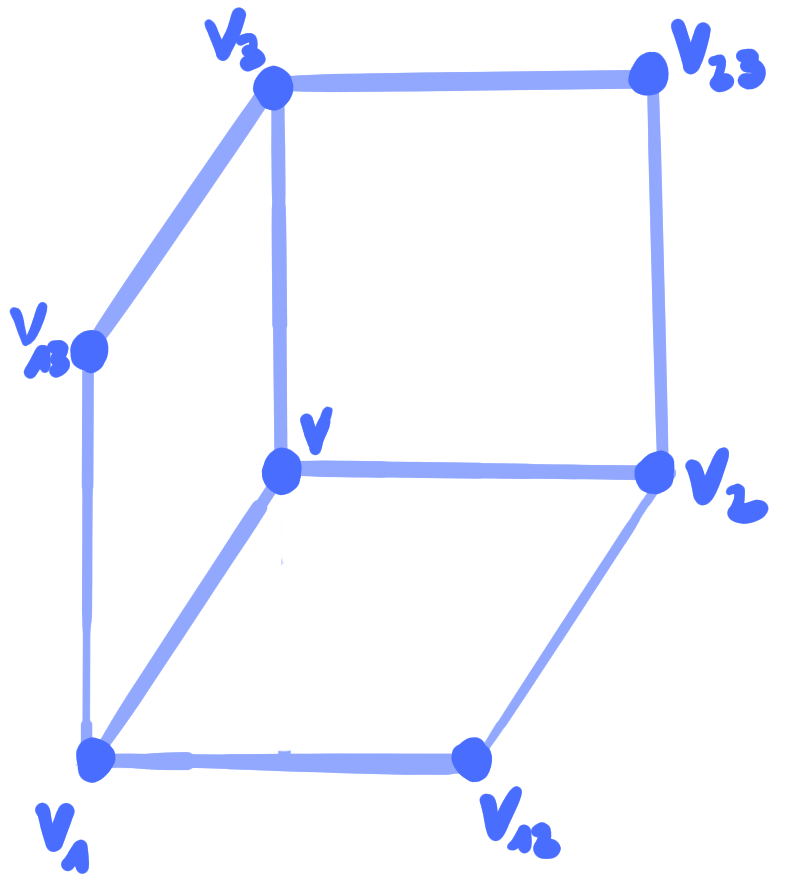
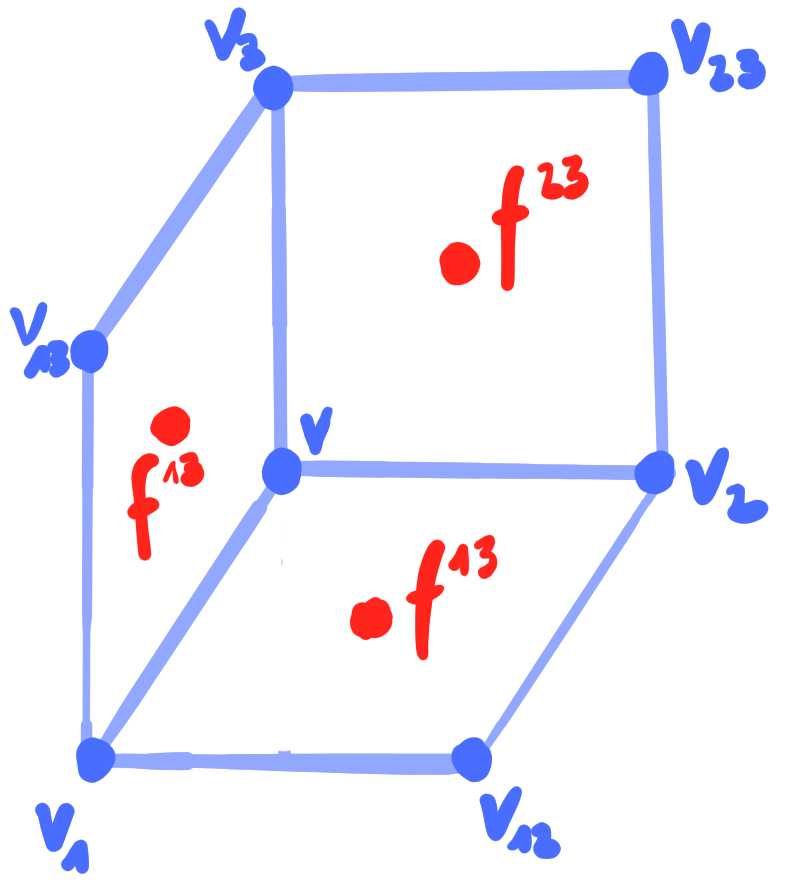
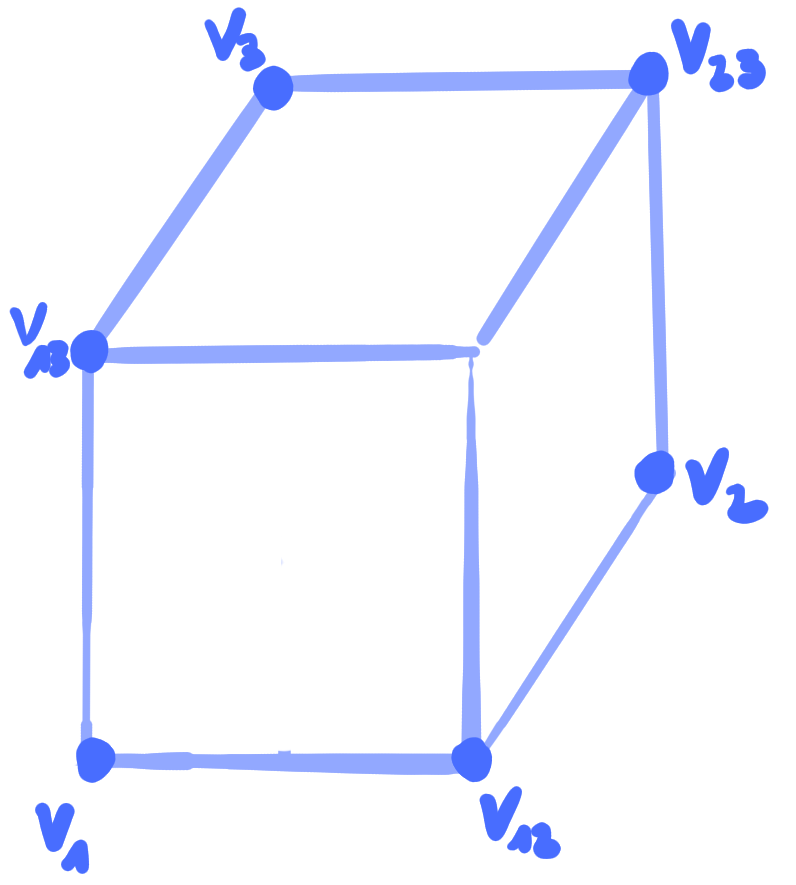
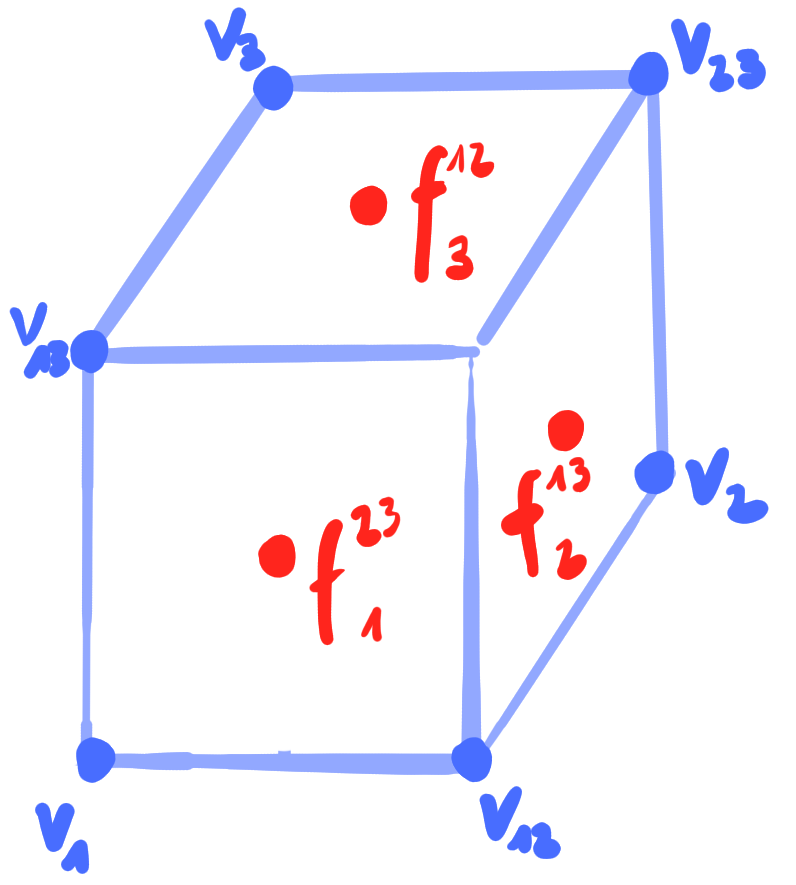
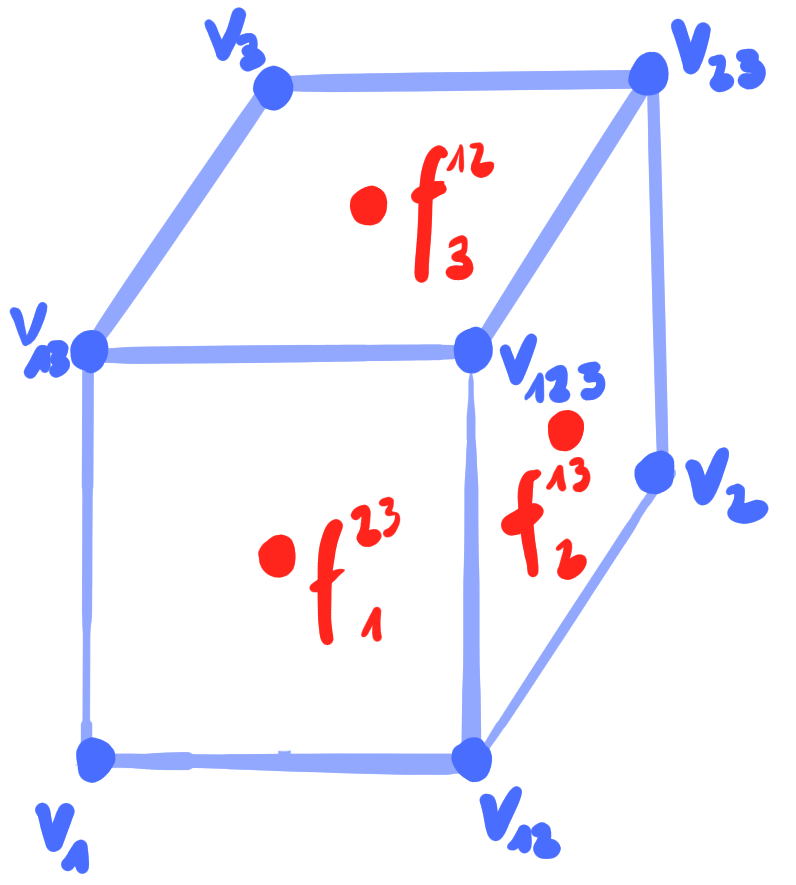
For conjugate binets the polarity condition is equivalent to $ ~\square b(d) \subset b(d)^\perp. $
\[ \scriptsize \begin{aligned} \square b(f_3^{12}) &= b(v_{23}) \vee b(v_{3}) \vee b(v_{13})\\ &\subset \square b(v_{23})^\perp \vee \square b(v_{3})^\perp \vee \square b(v_{13})^\perp = (\square b(v_{23}) \cap \square b(v_{3}) \cap \square b(v_{13}))^\perp = b(f^{12}_3)^\perp \end{aligned} \]
\[ \scriptsize \begin{aligned} \square b(v_{123}) &= b(f_3^{12}) \vee b(f_2^{13}) \vee b(f_1^{23})\\ &\subset \square b(f_3^{12})^\perp \vee \square b(f_2^{13})^\perp \vee \square b(f_1^{23})^\perp = (\square b(f_3^{12}) \cap \square b(f_2^{13}) \cap \square b(f_1^{23}))^\perp = b(v_{123})^\perp. \end{aligned} \]
Recall: Principal binets in $\R^3$ can be lifted to polar conjugate binets in $\R\mathrm{P}^4$.
Corollary: Principal binets in $\R^3$ are a consistent reduction of conjugate binets in $\R^3$.
The end
Thank you!