Typicality in Classical
and Quantum Information Theory |
Content
- 1 Introduction
- 2 Setup and Basic Concepts
- 3 Sanov's theorem, the ergodic case
- 4 Sanov's theorem, the stationary case
- 5 Sanov's theorem: A cradle of fundamental results in inf-theory
- 5.1 Shannon-McMillan, the ergodic case
- 5.2 Shannon-McMillan for stationary states
- 5.3 Kaltchenko-Yangs universality theorem for stationary states
- 5.4 Stein's lemma for stationary states
- 6 Proof of Sanov's theorem, the ergodic case
- 6.1 The case of just 2 states and (Stein's lemma)
- 6.2 from Stein's lemma to Sanov
- 6.3 *-mixing implies the HP-condition
- 7 proof of Sanov's theorem, the stationary case
- 8 references
1 Introduction
Classical spin chain: typical subsets, Shannon McMillan
  |
| |
  |
| |
  |
| |
  |
| |
  |
| |
  |
|
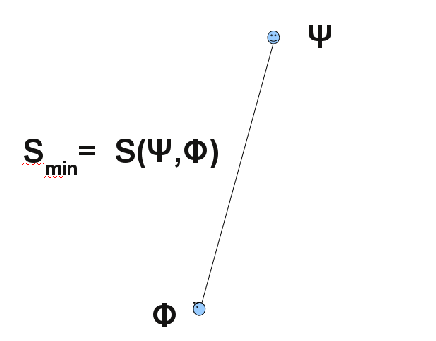
Given two states and .
Is there a sequence of -typical sets such that ?
Answer yes. But the convergence to zero can not be too fast. The optimal rate of convergence is given by an exponential law, where the exponent is the relative entropy density of the two states:
This is the content of Stein's lemma.
The problem in hypothesis testing:
Which one of the 2 states and is the better description of the observed data?
To answer this question, the set of n spin configurations is partitioned into the test set and its complement, such that . The closer to , the better the test.
2. Question: (interesting for compression of data)
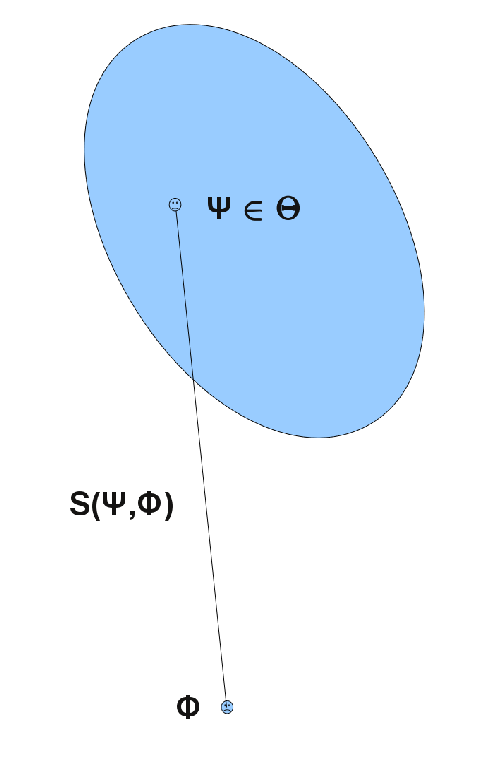
Is there a universal sequence of typical small sets for any state?
Answer is yes if rephrased in a more intelligent way: Given , is there a sequence of subsets which are typical for all states with entropy ?.
Proof for iid states e.g. by Lempel-Ziv compression algorithm.
Quantum Analog: Kaltchenko-Yang (see 8).
Note: This question is a combination of question 1 and 2.
Given
|
|
|
|
Is there a sequence of sets such that
|
|
|
|
Answer yes:
Provided: Convergence to not too fast
Optimal convergence: exponential law
Best exponent: (rel.entropy).
Remark on Classical - Quantum
  |
|
  |
|
  |
|
  |
|
Classical algebra of phase space functions (diagonal matrices) is abelian subalgebra of quantum algebra (full matrix algebra).
|
|
|
|
|
|
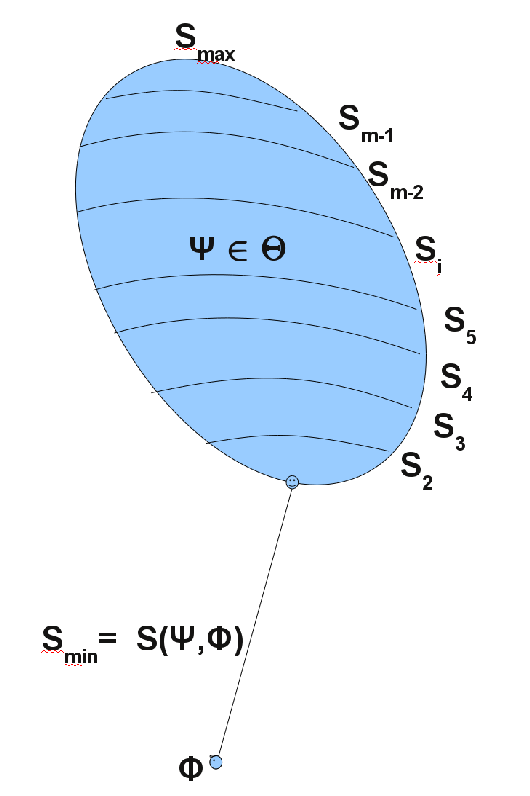
2 to 3: Slice the set along level sets.
2 Setup and Basic Concepts
Def: Discrete Information Source
  |
| |
  |
| |
  |
| |
  |
| |
  | | |
  |
| |
  |
| |
  |
| |
  |
| |
  |
| |
  |
|
Def: Stationary, Ergodic, IID States
  |
|
  |
|
  |
|
Def: entropy, relative entropy
  |
For stationary states entropy is subadditiv. Hence its rate converges: | ||
  |
and its rate by provided the limit exists. |
  |
| |
  |
| |
  |
| |
  |
| |
  |
|
sufficient condition for HP (discussed later)
ergodic and -mixing is HP.
Def: -mixing
A stationary state on
is called -mixing if for each there
exists an such that for each
3 Sanov's theorem, the ergodic case
Theorem (Sanov, ergodic, for classical case see (8):
Let be a state on and .
Statements and are equivalent:
|
| ||||||||
|
|
Remarks:
  |
| |
  |
|
Note about Sanov's theorem and hypothesis testing:
The test sequence of projectors defines a sequence of quantum-observables
with outcome and . It is interpreted as the quantum analog of
test sets in hypothesis testing. For that reason we use the terminology
test sequence of projectors.
For a discussion of quantum hypothesis testing and in its relation to the Q-Sanov theorem see the articles by K. M. R. Audenaert , M. Nussbaum , A. Szkoła , F. Verstraete 8. and M.Nussbaum and A.Szkola .
4 Sanov's theorem, the stationary case
Can be reduced to the ergodic case.
Recall:
|
| |||||||
|
| |||||||
|
|
Notation
  |
| |
  |
|
Theorem (Sanov, stationary):
Let
  |
|
  |
|
  |
|
Then
  |
| |
  |
| |
  |
|
Remarks:
  |
| |
  |
|
5 Sanov's theorem: A cradle of fundamental results in inf-theory
5.1 Shannon-McMillan, the ergodic case
Theorem (Shannon-McMillan, the ergodic case)
Consider an ergodic state .
Then
|
| ||||
|
|
Proof of the statement:
Sanov, ergodic case Shannon McMillan, ergodic case:
1. Choice
equipartition (tracial state):
2. is HP:
3. :
4. for large:
5. for large:
5.2 Shannon-McMillan for stationary states
Theorem (Shannon-McMillan, for stationary states)
Consider a stationary state
Then
|
| ||||
|
|
Remarks:
1. in the stationary case equipartition does not hold!
2. The relevant entropy in Sanov's theorem for
stationary states is not the mean entropy but the essential infimum of the ergodic
constituents of all states in .
Proof of the statemtent:
Sanov, stationary case
Shannon McMillan, the stationary case:
5.3 Kaltchenko-Yangs universality theorem for stationary states
Theorem (Kaltchenko-Yang, for stationary states)
Let
Then
|
| ||||
|
is the optimal lower bound: |
Proof of the statemtent:
Sanov, stationary case Kaltchenko-Yang theorem:
5.4 Stein's lemma for stationary states
Theorem (Stein's lemma for stationary null hypothesis)
Let and
such that for
-almost all the pair is HP.
Then
|
| ||||
|
|
Proof of the statement:
Sanov, stationary case Stein's lemma, stationary case:
6 Proof of Sanov's theorem, the ergodic case
6.1 The case of just 2 states and (Stein's lemma)
Proposition 1:
-typical test sequence of projectors in terms of
spectral data
(the relative equipartion theorem)
Assume ergodic and arbitrary states on ,
HP and .
Consider the family of -spectral projectors
denotes the eigen-projection of
for eigenvalue .
Then
Outline of proof:
1. is the expectation value of the random variable with probability distribution :
2. :
3. :
4. :
5. Step 3 and 4 imply the statement of propopsition 1:
Proposition 2:
maximally separating sequence of projections
Assumption as in proposition 1 (6.1). Furthermore assume the test sequence of
projectors is optimally -typical in the sense:
| (29) | (29) |
Then there is a sequence such that the spectral projectors satisfy
Hence is an optimally separating sequence of projections.
Outline of proof:
1. denotes a state, two projectors. Then :
2. one gets
3. :
4. :
5. :
6. :
Proposition 3:
lower bound for any separating sequence of projections of large -measure
Assumption as in proposition 1 (6.1),. Let be a
test sequence of projectors such that for large.
Then
Proposition 4:
Conclusion from (6.1 and 6.16.1), Stein's lemma
Considere ergodic and arbitrary states on and assume
is HP (2)
Then
6.2 from Stein's lemma to Sanov
Construction of -universal sequencies of typical projections:
The main objective is the proof of formula (3). It asserts
the existence of -typical test sequence of projectors for any
which is maximally non typical with respect to , in other words maximally
separating.
Here is a sketch of the strategy of proof:
  |
|
  |
|
  |
|
(For details see (BDKSSS 20078).
6.3 *-mixing implies the HP-condition
-mixing implies the HP-condition. Hence Sanov's theorem holds under the condition of -mixing. This is not astonishing since -mixing states are by definition quite close to block-iid states.
The proof of the fact that -mixing implies the HP-condition is an elaboration of some results by Hiai and Petz (Hiai-Petz 1991, 8). For details see reference (Bjelakovic et al. 8).
8 references
K.M.R.Audenaert, M.Nussbaum, A. Szkola, F.Verstraete: Asymptotic Error Rates in Quantum Hypothesis Testing, Commun.Math.Phys. 279, 251-283 (2008)
I. Bjelakovic, T. Krüger, Ra. Siegmund-Schultze, A. Szkola, The Shannon-McMillan theorem for ergodic quantum lattice systems, Invent. Math. 155 (1), 203-222 (2004)
I. Bjelakovic, J.-D. Deuschel, T. Krüger, R. Seiler, Ra. Siegmund-Schultze, A. Szkola: Typical support and Sanov large deviations fo correlated states. Commun. Math. Phys. 279, 559-584 (2008)
F. Hiai, D. Petz, The Proper Formula for Relative Entropy and its Asymptotics in Quantum Probability, Commun. Math. Phys. 143, 99-114 (1991)
A. Kaltchenko, E. H. Yang, Universal Compression of Ergodic Quantum Sources, Quant. Inf. and Comput. 3, 359-375 (2003)
M.Nussbaum, A. Szkola; Exponential error rates in multiple state discrimination on a quantum spin chain, J.Math.Phys. 51, 072203 (2010)
D. Ruelle: Statistical Mechanics, Benjamin Inc., 1969
I.N. Sanov, On the probability of large deviations of random variables, Mat. Sbornik 42, 11-44, 1957