5-Holes in point sets
We investiaged the minimum number of convex 5-holes in small point sets. The following table summarizes our knowledge on the values of $h_5(n)$ for small $n$. Here $h_5(n)$ denotes the minimum number of 5-holes among all sets of $n$ points and $h_5^*(n)$ denotes the minimum number of 5-holes among all generalized point sets of size $n$. We omit the entry for $h_5^*(n)$ if it coincides with the one for $h_5(n)$.| $n$ | $h_5(n)$ | $h_5^*(n)$ |
|---|---|---|
| 9 | 0 | |
| 10 | 1 | |
| 11 | 2 | |
| 12 | 3 | |
| 13 | 3 | |
| 14 | 6 | |
| 15 | 9 | |
| 16 | 11 | |
| 17 | 15 | |
| 18 | ..21 | |
| 19 | ..26 | |
| 20 | ..33 | |
| 21 | ..39 | |
| 22 | ..46 | ..45 |
| 23 | ..53 | ..52 |
| 24 | ..62 | ..60 |
| 25 | ..72 | ..69 |
| 26 | ..80 | ..77 |
| 27 | ..90 | ..87 |
| 28 | ..103 | ..99 |
| 29 | ..119 | ..115 |
| 30 | ..137 | ..129 |
| 31 | ..154 | ..147 |
| 32 | ..175 | ..167 |
| 33 | ..195 | ..190 |
| 34 | ..226 | ..216 |
| 35 | ..251 | ..237 |
| 36 | ..268 | ..261 |
| 37 | ..291 | |
| 38 | ..309 | |
| 39 | ..351 | |
| 40 | ..373 | ..348 |
| 50 | ..731 | |
| 60 | ..1244 | |
| 70 | ..1875 |
Exact Values and Lower Bounds
Every set $P$ of $n$ points with $k=h_5(P)$ 5-holes implies that $h_5(n) \le k$, where $h_5(P)$ denotes the number of $5$-holes in $P.$ To show $h_5(n)=k$, it suffices to find a set of $n$ points with $k$ 5-holes and then show that there is no point set $P$ with $h_5(P) < k$. To determine the exact value of $h_5(n)$ for small values of $n$, we have two independent implementations. The basic idea behind both programs is to either find a set of $n$ points with at most $k$ 5-holes or show that no such point set exists. The first implementation, which was already described in my Bachelor's thesis, is based on the program for generating the database of order types. Points are iteratively added outside the convex hull of a generalized point set $P$ using abstract extension unless $|P|=n$ or $h_5(P) > k$. If $h_5(P) > k$, then any further point cannot decrease the number of 5-holes as we only add points outside of the convex hull. Our second implementation generates an integer linear program (ILP) instance to decide whether $h_5(P) \le k$, which then can be solved using GLPK package (GNU Linear Programming Kit). GLPK allows to transform the problem into a CNF-SAT instance, which can then be solved by Minisat (which is fully integrated in GLPK). We remark that one can also manually decode (bounded) integer variables by binary variables representing the binary-represention. The idea is to use binary variables- for each ordered triple of three points (whether it is positively or negatively oriented),
- for each four points (whether they are in convex position or not), and
- for each three points (whether they form a $3$-hole).
The sourcecode of the second implementation can be downloaded here. It can be used to verify the values $h_5(9)=0$, $h_5(10)=1$, $h_5(11)=2$, $h_5(12)=3$, $h_5(13)=3$, $h_5(14)=6$, $h_5(15)=9$, $h_5(16)=11$, and $h_5(17)=15$. The values of $h_5(9)$ and $h_5(10)$ were already determined by Harborth and the values of $h_5(11)$ and $h_5(12)$ were determined by Dehnhardt. The values of $h_5(13)$, $h_5(14)$, and $h_5(15)$ were determined in my Bachelor's thesis, where also $h_5(16) \in \{ 10,11\}$ was shown. The exact values $h_5(16)=11$ and $h_5(17)=15$ were determined with the aid of the SAT solver cadical. Click here for more information on the SAT model. Concerning the running time of the computations:
- one cpu hour to determine the values of $h_5(n)$ for $n \le 14$,
- 2 cpu days to verify $h_5(15) > 8$,
- 16 cpu days to verify $h_5(16) > 10$.
- 140 cpu days to verify $h_5(17) > 14$.
Upper Bounds
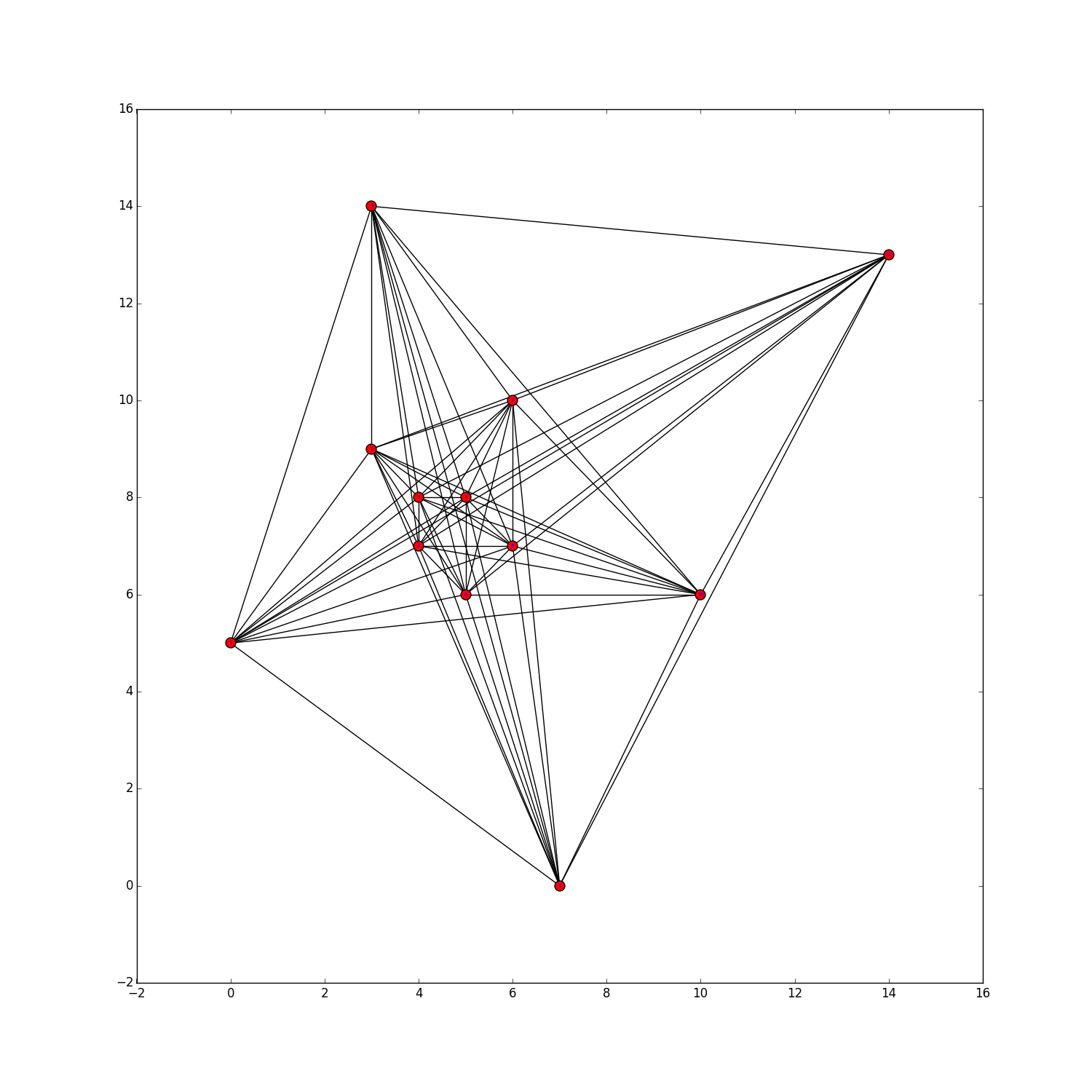
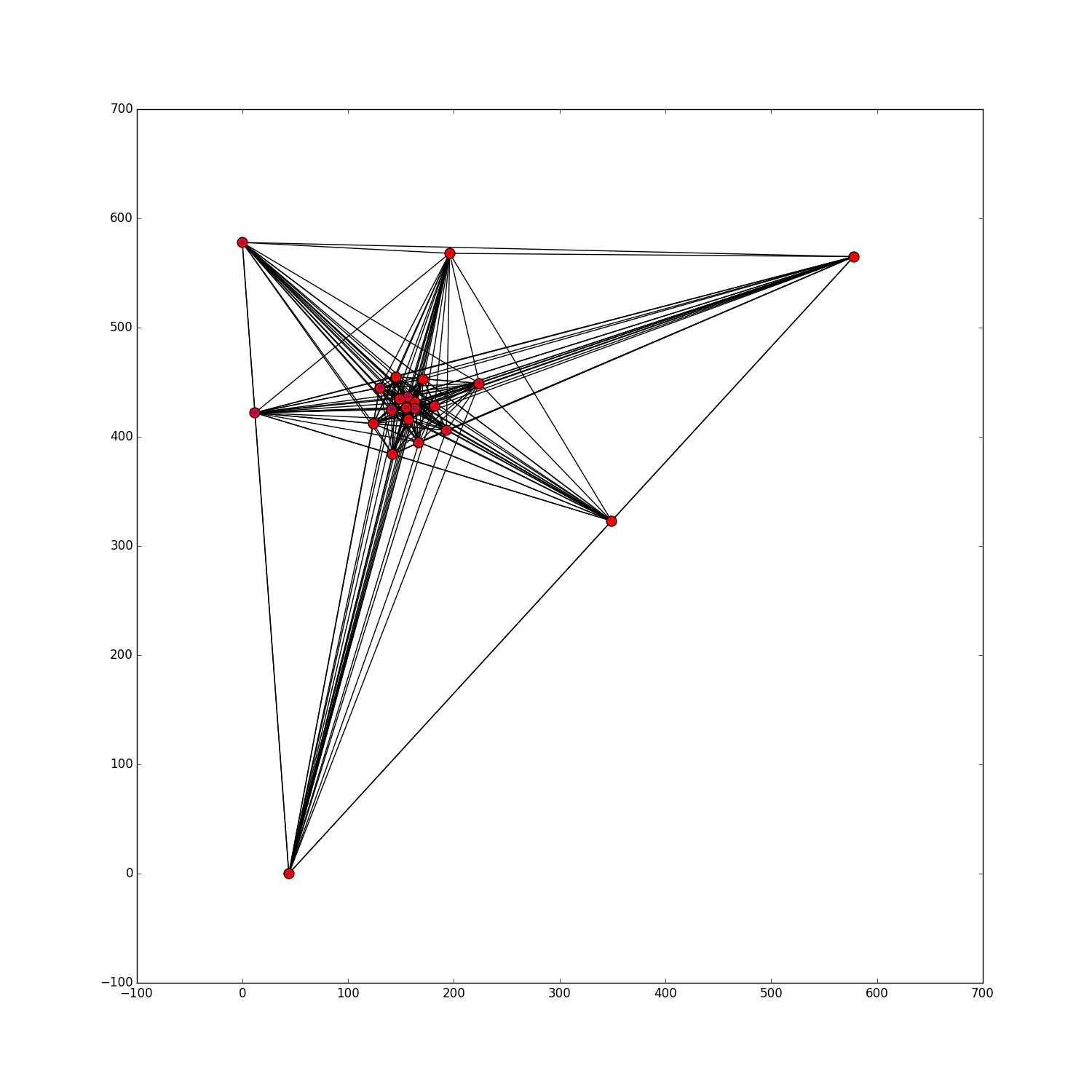
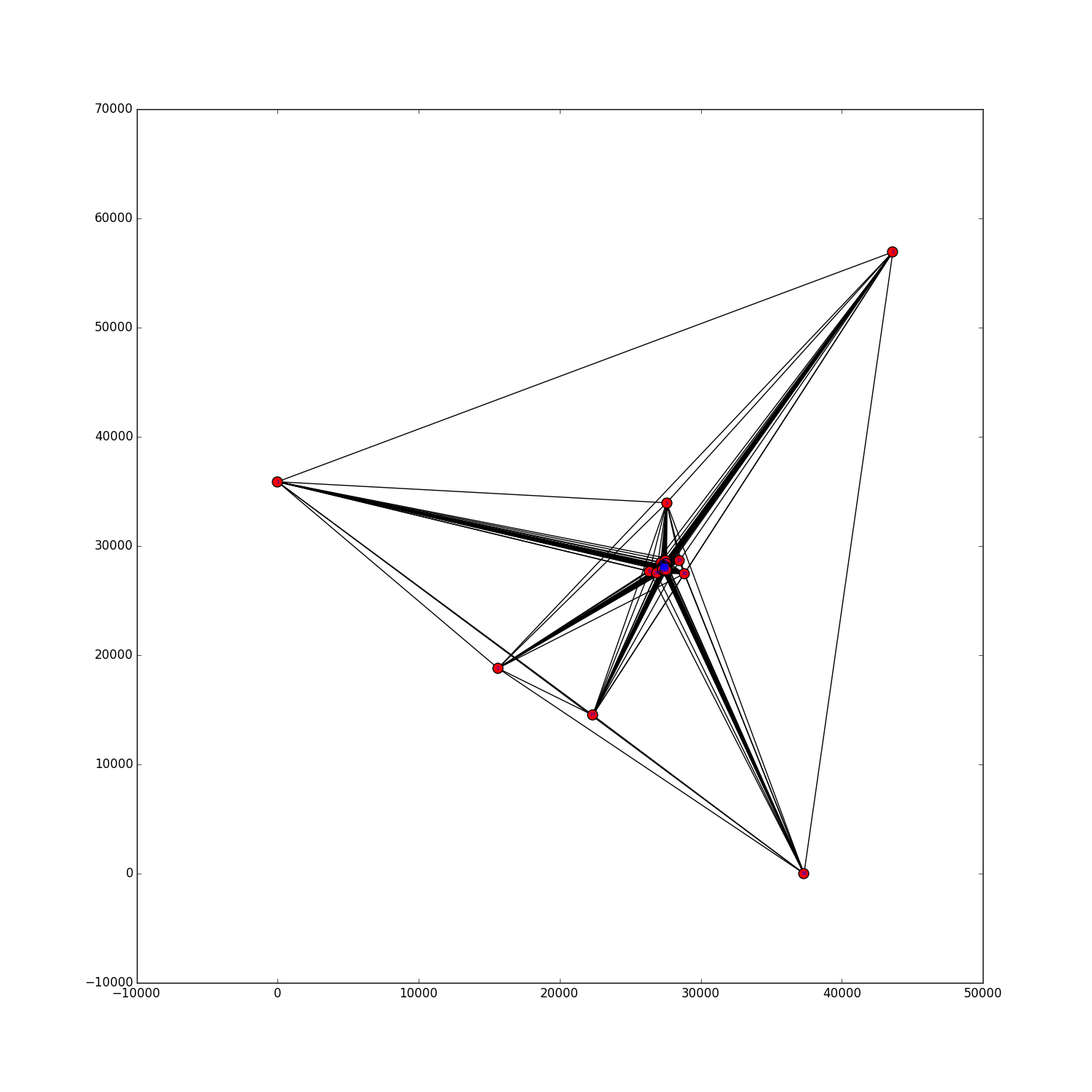
Here we present sets of $n$ points for $n \le 40$ and $n=50,60,70$, with a small number of 5-holes (probably not minimum). Moreover, for $22 \le n \le 40$ we present some generalized point sets encoded by their small lambda matrices. For $n \le 25$, we can prove that the found generalized point sets are not realizable by point sets in the plane as they violate the Grassman-Pluecker relations. To be more precise, non-realizabilty of certain generalized point subsets was shown using GLPK with "exact arithmetics" (i.e., simplex method on rational numbers). However, even though these generalized point sets are not realizable, this does not imply that no (Euclidean) point set with that amount of 5-holes exists. For the generalized point sets we provide a visualization of their dual pseudoline arrangements.The filename describes the number of points and the number of 5-holes. For example data/n0029c5h000115.psz shows a set of $n=29$ points with $h_5=115$ 5-holes.