Gegeben sei eine invertierbare Matrix
 mit mit
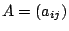 , ,
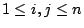 und ein Vektor und ein Vektor
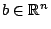 . Dann ist ein lineares Gleichungssystem von der Form . Dann ist ein lineares Gleichungssystem von der Form
bzw.
Ziel ist es nun einen Vektor
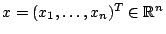 zu bestimmen, der diese Gleichungen erfüllt. Ein solcher Vektor heißt dann Lösung des Gleichungssystems.
Ein Verfahren zur Bestimmung der Lösung von linearen Gleichungssystemen ist das Gauß'sche Eliminationsverfahren. Die Idee ist, das gegebene Gleichungssystem durch bestimmte Umformungen in die folgende gestaffelte Form zu bringen: zu bestimmen, der diese Gleichungen erfüllt. Ein solcher Vektor heißt dann Lösung des Gleichungssystems.
Ein Verfahren zur Bestimmung der Lösung von linearen Gleichungssystemen ist das Gauß'sche Eliminationsverfahren. Die Idee ist, das gegebene Gleichungssystem durch bestimmte Umformungen in die folgende gestaffelte Form zu bringen:
Aus dieser Form lässt sich die Lösung des Systems sehr leicht durch Rückwärtsauflösen berechnen (falls
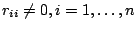 ): ):
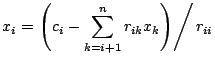 für 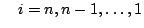
- Vertauschen von Zeilen/Spalten;
- Multiplikation einer kompletten Zeile mit einer von null verschiedenen reellen Zahl;
- Addition eines Vielfachen einer Zeile zu einer anderen.
Im Folgenden wird nun das Verfahren beschrieben.
Setze  und und 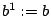 . Seien nun schon . Seien nun schon 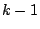 Schritte durchgeführt, dann hat das System die Form Schritte durchgeführt, dann hat das System die Form
mit
Der 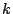 -te Schritt geht dann wie folgt: -te Schritt geht dann wie folgt:
- Wähle ein
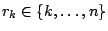 mit mit
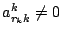 und vertausche die und vertausche die 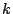 -te und -te und 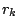 -te Zeile von -te Zeile von 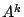 (und (und 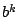 ), um ), um 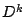 zu erhalten. zu erhalten.
- Subtrahiere das
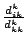 -fache der -fache der 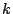 -ten Zeile von der -ten Zeile von der  -ten für -ten für
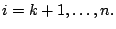
- Bezeichne die so erhaltene Matrix mit
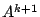 und den Vektor mit und den Vektor mit 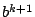
Das in Schritt 1 gewählte Element
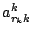 wird auch Pivotelement genannt. Durch geschickte Wahl des Pivotelements kann man gegebenenfalls numerisch bessere Ergebnisse bei der Durchführung des Verfahrens erzielen. Gängige Strategien zur Wahl des Pivotelements sind die Folgenden:
Während der Durchführung des Gauß-Algorithmus können sich Rundungsfehler anhäufen, und die berechnete Lösung wird auch Pivotelement genannt. Durch geschickte Wahl des Pivotelements kann man gegebenenfalls numerisch bessere Ergebnisse bei der Durchführung des Verfahrens erzielen. Gängige Strategien zur Wahl des Pivotelements sind die Folgenden:
Während der Durchführung des Gauß-Algorithmus können sich Rundungsfehler anhäufen, und die berechnete Lösung
 muss nicht mehr viel mit der wahren Lösung muss nicht mehr viel mit der wahren Lösung 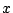 zu tun haben. Wie stark die Abweichung maximal sein kann, hängt unmittelbar von der Kondition der Matrix zu tun haben. Wie stark die Abweichung maximal sein kann, hängt unmittelbar von der Kondition der Matrix 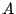 ab. Die Kondition ist dabei definiert durch ab. Die Kondition ist dabei definiert durch
Man kann nun folgendes zeigen:
Sei 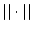 eine Vektornorm und eine Vektornorm und 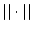 eine dazu verträgliche Matrixnorm. Ist die rechte Seite eine dazu verträgliche Matrixnorm. Ist die rechte Seite
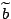 im Vergleich zur tatsächlichen rechten Seite im Vergleich zur tatsächlichen rechten Seite 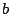 gestört, und löst dann gestört, und löst dann
 das Gleichungssystem das Gleichungssystem
dann gilt für die relative Änderung der Lösung die (i.A. zu pessimistische) Abschätzung
Die Aussagen werden schwieriger falls auch Störungen in 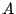 berücksichtigt werden. Das analoge Ergebnis lautet dann: berücksichtigt werden. Das analoge Ergebnis lautet dann:
Sei 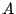 invertierbar, und für die gestörte Matrix gelte invertierbar, und für die gestörte Matrix gelte
 . Dann ist . Dann ist
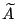 invertierbar, und mit invertierbar, und mit
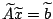 gilt gilt
Das folgende Programm löst lineare Gleichungssysteme mit dem Gauß'schen Eliminationsverfahren. Wird nur eine Pivotisierungsstrategie für ein Gleichungssystem mit 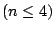 ausgewählt, zeigt das Programm die konkrete Durchführung des Verfahrens. Wählt man dagegen mehrere Strategien oder ein größeres Gleichungssystem, so werden die Ergebnisse genauer diskutiert. Es besteht außerdem die Möglichkeit, das Gauß-Verfahren mit verschiedenen Mantissenlängen durchzuführen, so dass Rundungsfehler besser deutlich werden. ausgewählt, zeigt das Programm die konkrete Durchführung des Verfahrens. Wählt man dagegen mehrere Strategien oder ein größeres Gleichungssystem, so werden die Ergebnisse genauer diskutiert. Es besteht außerdem die Möglichkeit, das Gauß-Verfahren mit verschiedenen Mantissenlängen durchzuführen, so dass Rundungsfehler besser deutlich werden.
Top
|
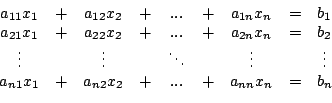
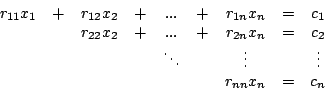
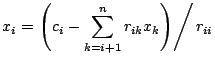 für
für
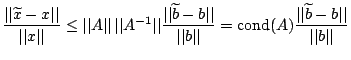
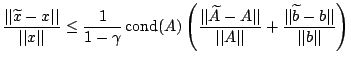
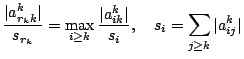
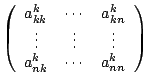 das betragsmäßig maximale Element suchen. Dieses muss man dann durch Zeilen- und Spaltentausch an die Stelle
das betragsmäßig maximale Element suchen. Dieses muss man dann durch Zeilen- und Spaltentausch an die Stelle