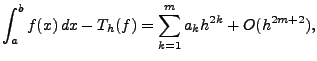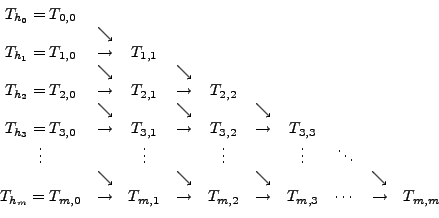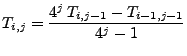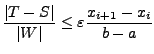Integration
Übersicht
Allgemeine Integrationsaufgabe
Die Grundaufgabe dieses Kapitels ist zu
einer gegebenen Funktion
![$ f\in C[a, b]$](img1.png) das Integral
numerisch zu bestimmen. Zur Lösung dieser Aufgabe wurden die
verschiedensten Algorithmen entwickelt.
Ein Ansatz zur numerischen Integration einer Funktion
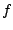 sind die sogenannten
Newton-Cotes-Formeln. sind die sogenannten
Newton-Cotes-Formeln.
Zunächst werden 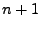 paarweise verschiedene
Stützstellen paarweise verschiedene
Stützstellen 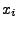 gewählt mit gewählt mit
wobei
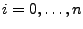 ist.
Mit diesen Stützstellen wird dann das zur Funktion
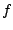 gehörige, eindeutig bestimmte
Interpolationspolynoms gehörige, eindeutig bestimmte
Interpolationspolynoms 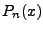 vom Grad vom Grad 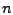 unter Verwendung der Lagrange-Polynome unter Verwendung der Lagrange-Polynome
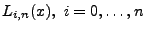 bestimmt. Man
erhält also: bestimmt. Man
erhält also:
Als Approximation an das Integral von 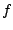 wird dann das
Integral des Interpolationspolynom 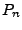 genommen.
Also:
Der Vorteil dieser Darstellung ist, dass das Integral der
Lagrange-Polynome nur abhängig ist von den Parametern
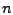 und 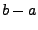 . Man erhält:
Die Werte der Gewichte 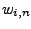 kann man aus der
folgenden Tabelle entnehmen. Der Name der entsprechenden Regel ist
in der letzten Spalte angegeben.
Da bei größeren Werten von 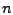 auch negative
Gewichte auftauchen, werden die entsprechenden Formeln numerisch
unbrauchbar. Um die Genauigkeit dieser Approximation dennoch zu
erhöhen, teilt man zunächst das gesamte Intervall in
kleinere Teilintervalle. Auf diesen Teilintervallen wendet man nun
die Regeln an und addiert dann die ermittelten Werte. Sind die
Teilintervalle gleich groß, so erhält man die sogenannten
Summenregeln.
Exemplarisch wird hier die Trapezsumme vorgestellt.
Es seien folgende Stützstellen gegeben:
wobei
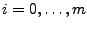 und
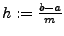 ist. Die Trapezsumme ist
dann
Top
Romberg Integration
Die Romberg Integration beruht auf
der oben vorgestellten Trapezsumme. Man kann zeigen, dass für
die Trapezsumme einer 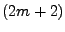 -mal stetig
differenzierbaren Funktion folgende Fehlerdarstellung gilt:
wobei 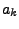 von 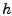 unabhängige
Konstanten sind. Insbesondere ist der Fehler bei der Trapezsumme
vom Typ 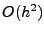 . Eine Herleitung des Romberg
Verfahrens besteht darin die Faktoren 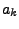 durch
geschickte Addition zu eliminieren und so die Fehlerordnung zu
erhöhen.
Dazu werden zunächst die Treppensummen
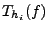 für für
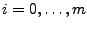 mit mit
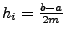 bestimmt. Nun wird das
folgende Romberg-Schema angewandt: bestimmt. Nun wird das
folgende Romberg-Schema angewandt:
Dabei ergibt sich  durch die folgende
Additionsformel:
Damit lässt sich zeigen, dass in jeder Spalte die Ordnung des
Fehlers um 2 erhöht wird, in der 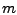 -ten Spalten
also ein Fehler vom Typ
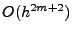 vorliegt.
Man kann ebenso zeigen, dass die zweite Spalte der Simpsonsumme
entspricht, d.h. 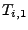 entspricht der Simpsonsumme
zur Weite entspricht der Simpsonsumme
zur Weite 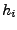 . .
Das folgende Programm führt die Rombergintegration aus. Man
kann Spalten aus dem obigen Rombergschema auswählen und sich
den jeweiligen Fehler zum exakten Integral anzeigen lassen.
Außerdem kann man sich den Fehler der Diagonalen, d.h. von
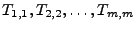 ausgeben
lassen. ausgeben
lassen.
Top
Adaptive Integration
Die Romberg Integration liefert bei
glatten Funktionen sehr gute Approximationen an das Integral.
Jedoch bei stark variierenden Funktionen ist die Romberg
Integration eher ineffektiv. Man würde dann lieber nicht
äquidistante Stützstellen je nach dem Verhalten von
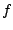 verwenden. Diesen Ansatz verfolgt die
adaptive Integration.
Zur Erläuterung des Verfahrens wird das folgende
Teilintervall
![$ [ x_i , x_{i+1} ]$](img37.png) betrachtet. Auf diesem
Intervall wird sowohl die Treppensumme betrachtet. Auf diesem
Intervall wird sowohl die Treppensumme 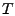 , als auch die
Simpsonregel , als auch die
Simpsonregel 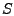 berechnet. Anschließend wird
geprüft, ob folgende Bedingung erfüllt ist. berechnet. Anschließend wird
geprüft, ob folgende Bedingung erfüllt ist.
Hierbei ist 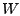 ein sehr grober Schätzwert
für das exakte Integral, welcher die Größenordnung
erfasst, und
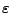 die geforderte relative
Genauigkeit. Wird die obige Bedingung erfüllt, so wird
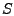 als Approximation auf diesem Teilintervall
akzeptiert und das nächste Teilintervall betrachtet.
Wird die obige Bedingung nicht erfüllt, so wird das
Intervall
![$ [ x_i , x_{i+1} ]$](img37.png) in die zwei Teilintervalle in die zwei Teilintervalle
![$ [ x_i , \tau ]$](img43.png) und und
![$ [ \tau , x_{i+1} ]$](img44.png) aufgeteilt, wobei aufgeteilt, wobei
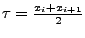 ist.
Anschließend wird diese Methode zunächst auf das
Intervall ist.
Anschließend wird diese Methode zunächst auf das
Intervall
![$ [ x_i , \tau ]$](img43.png) und dann auf das Intervall und dann auf das Intervall
![$ [ \tau , x_{i+1} ]$](img44.png) angewendet. angewendet.
Das folgende Programm führt die adaptive Integration aus.
Man kann sowohl die relative Genauigkeit
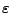 , als auch die maximale Anzahl an
Stützstellen angeben. Anschließend wird die Bestimmung
der Stützstellen als Slideshow angezeigt. , als auch die maximale Anzahl an
Stützstellen angeben. Anschließend wird die Bestimmung
der Stützstellen als Slideshow angezeigt.
Top
|
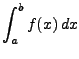
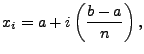
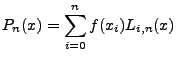
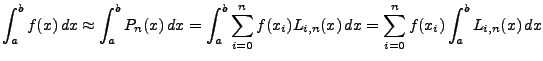
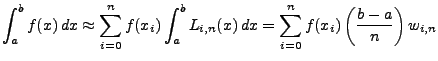
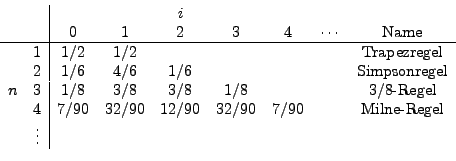
![$\displaystyle \int_a^b f(x) dx \approx T_h (f) := h \left[ \frac{1}{2}f( x_0 ) + \sum_{i=0}^{m-1} f( x_i ) + \frac{1}{2} f( x_m ) \right]$](img21.png)